« previous next »

Author Question: The number of customers at Winkies Donuts between 8:00a.m. and 9:00a.m. is believed to follow a ... (Read 65 times)

strangeaffliction

  • Hero Member
  • *****
  • Posts: 660
on: Jun 24, 2018
The number of customers at Winkies Donuts between 8:00a.m. and 9:00a.m. is believed to follow a Poisson distribution with a mean of 2 customers per minute.
 a. During a randomly selected one minute interval during this time period, what is the probability of 6 customers arriving to Winkies?
  b. What is the probability that at least 2 minutes elapse between customer arrivals?

Question 2

The multiple coefficient of determination is
 a. MSR/MST
  b. MSR/MSE
  c. SSR/SST
  d. SSE/SSR


amynguyen1221

  • Sr. Member
  • ****
  • Posts: 355
Reply #1 on: Jun 24, 2018
Answer to Question 1

a. .0120
b. .0183

Answer to Question 2

C


Related Topics

Need homework help now?

Ask unlimited questions for free

Ask a Question
« previous next »
 

Did you know?

Never take aspirin without food because it is likely to irritate your stomach. Never give aspirin to children under age 12. Overdoses of aspirin have the potential to cause deafness.

Did you know?

There are actually 60 minerals, 16 vitamins, 12 essential amino acids, and three essential fatty acids that your body needs every day.

Did you know?

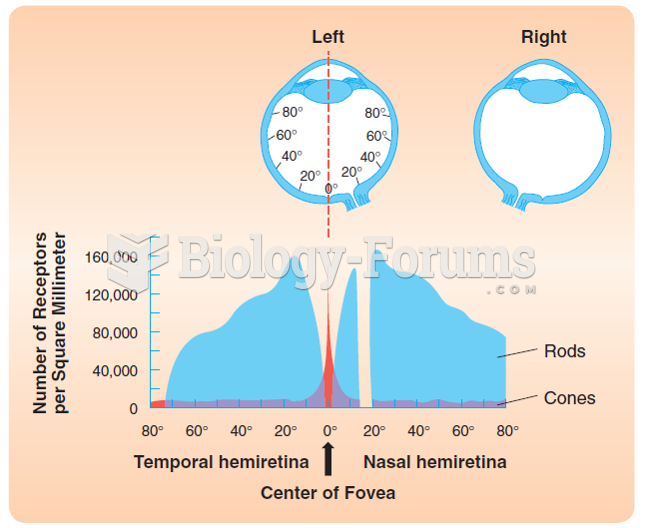
Signs and symptoms that may signify an eye tumor include general blurred vision, bulging eye(s), double vision, a sensation of a foreign body in the eye(s), iris defects, limited ability to move the eyelid(s), limited ability to move the eye(s), pain or discomfort in or around the eyes or eyelids, red or pink eyes, white or cloud spots on the eye(s), colored spots on the eyelid(s), swelling around the eyes, swollen eyelid(s), and general vision loss.

Did you know?

The average person is easily confused by the terms pharmaceutics and pharmacology, thinking they are one and the same. Whereas pharmaceutics is the science of preparing and dispensing drugs (otherwise known as the science of pharmacy), pharmacology is the study of medications.

Did you know?

The first war in which wide-scale use of anesthetics occurred was the Civil War, and 80% of all wounds were in the extremities.

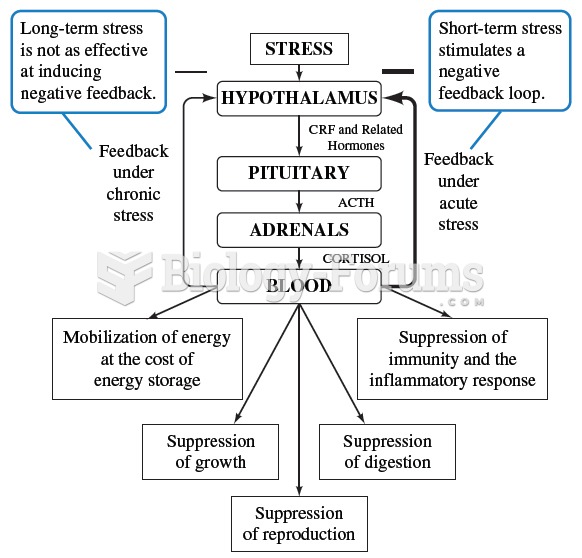Mammals posses a number of physiological pathways related to stress. One example is the hypothalamic Mammals posses a number of physiological pathways related to stress. One example is the hypothalamic
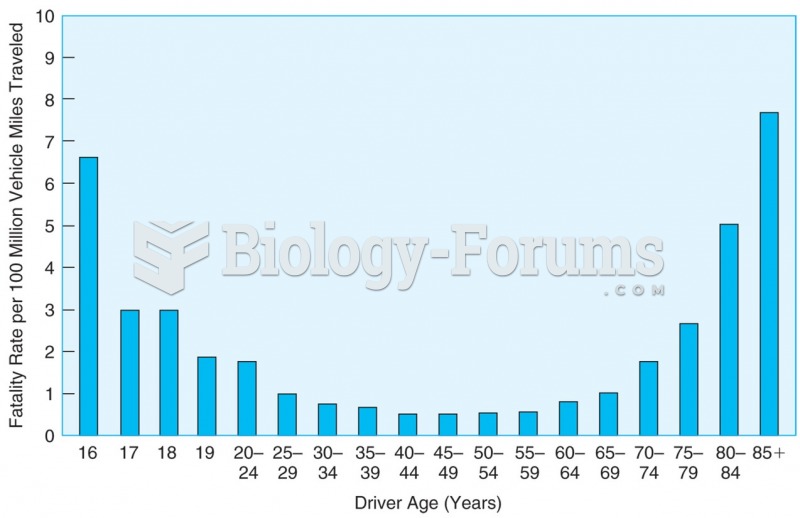When the number of miles traveled is considered, drivers under 25 years of age and those over 70 are ... When the number of miles traveled is considered, drivers under 25 years of age and those over 70 are ...
The distribution of cones and rods over the human retina. The figure illustrates the number of cones ... The distribution of cones and rods over the human retina. The figure illustrates the number of cones ...
Number Number
How would you write the number 120 in Babylonian? How would you write the number 120 in Babylonian?
Plot showing the number of genes on each human chromosome Plot showing the number of genes on each human chromosome
Video: Introduction to Breast Cancer

For a complete list of videos, visit our video library