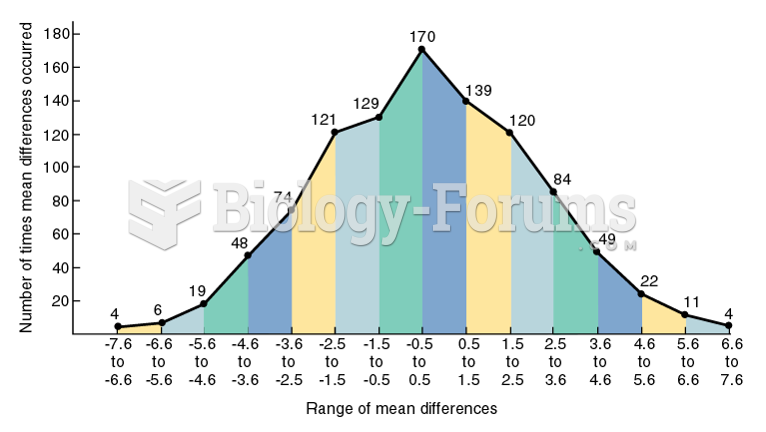
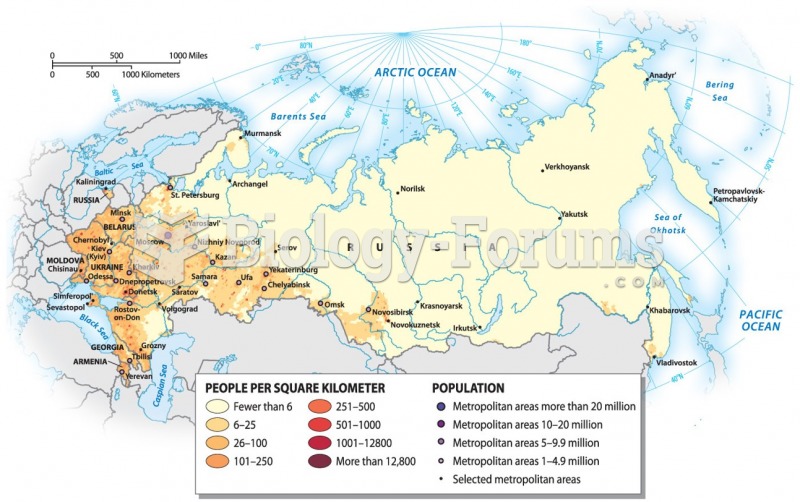
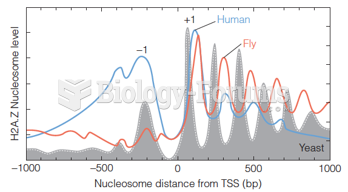
|
|
|
People who have myopia, or nearsightedness, are not able to see objects at a distance but only up close. It occurs when the cornea is either curved too steeply, the eye is too long, or both. This condition is progressive and worsens with time. More than 100 million people in the United States are nearsighted, but only 20% of those are born with the condition. Diet, eye exercise, drug therapy, and corrective lenses can all help manage nearsightedness.
When blood is deoxygenated and flowing back to the heart through the veins, it is dark reddish-blue in color. Blood in the arteries that is oxygenated and flowing out to the body is bright red. Whereas arterial blood comes out in spurts, venous blood flows.
The Romans did not use numerals to indicate fractions but instead used words to indicate parts of a whole.
Aspirin is the most widely used drug in the world. It has even been recognized as such by the Guinness Book of World Records.
Limit intake of red meat and dairy products made with whole milk. Choose skim milk, low-fat or fat-free dairy products. Limit fried food. Use healthy oils when cooking.