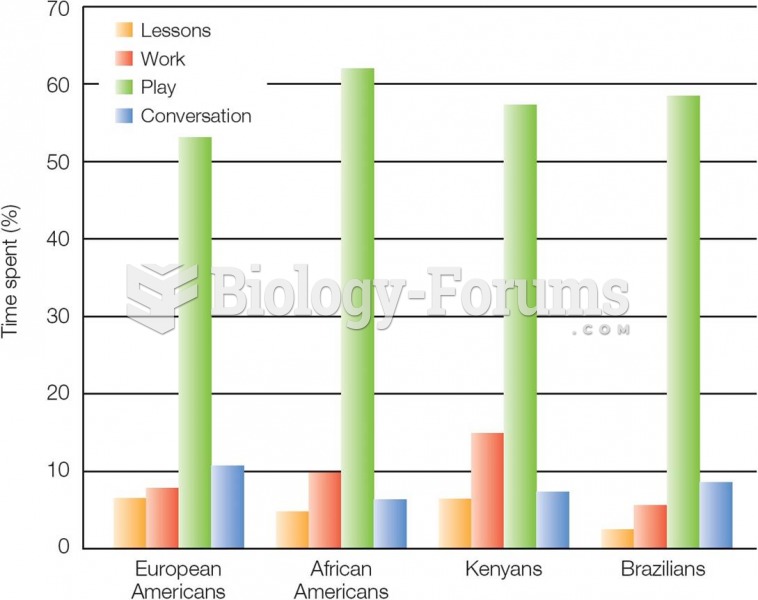
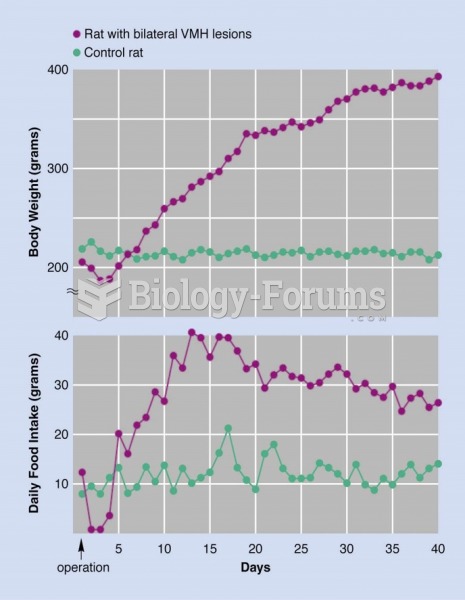
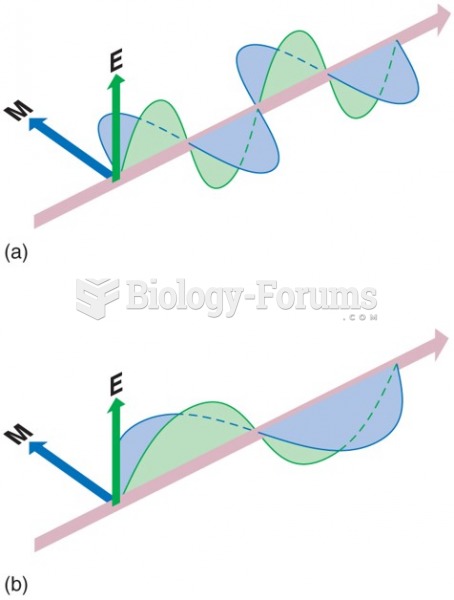
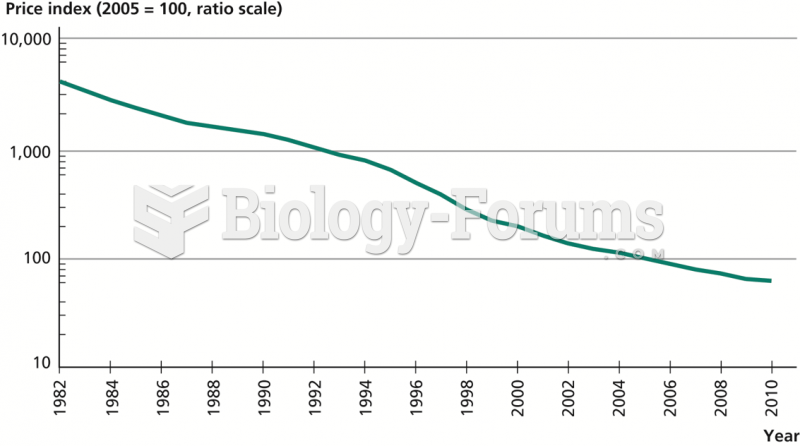
|
|
|
Oxytocin is recommended only for pregnancies that have a medical reason for inducing labor (such as eclampsia) and is not recommended for elective procedures or for making the birthing process more convenient.
Signs and symptoms that may signify an eye tumor include general blurred vision, bulging eye(s), double vision, a sensation of a foreign body in the eye(s), iris defects, limited ability to move the eyelid(s), limited ability to move the eye(s), pain or discomfort in or around the eyes or eyelids, red or pink eyes, white or cloud spots on the eye(s), colored spots on the eyelid(s), swelling around the eyes, swollen eyelid(s), and general vision loss.
When taking monoamine oxidase inhibitors, people should avoid a variety of foods, which include alcoholic beverages, bean curd, broad (fava) bean pods, cheese, fish, ginseng, protein extracts, meat, sauerkraut, shrimp paste, soups, and yeast.
Everyone has one nostril that is larger than the other.
Though the United States has largely rejected the metric system, it is used for currency, as in 100 pennies = 1 dollar. Previously, the British currency system was used, with measurements such as 12 pence to the shilling, and 20 shillings to the pound.