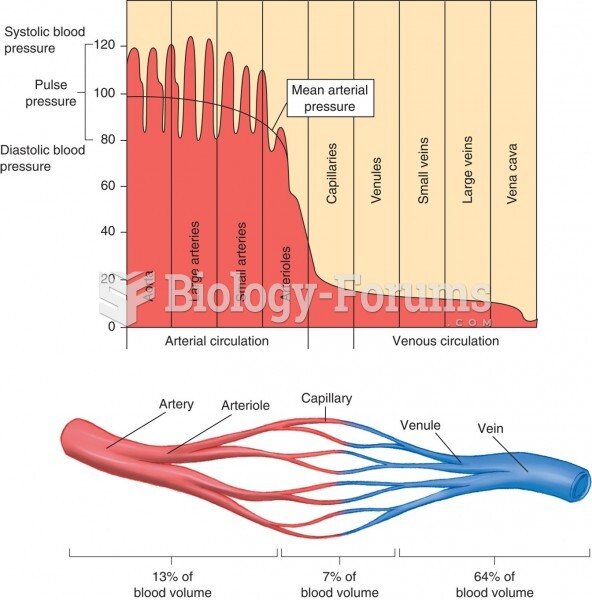
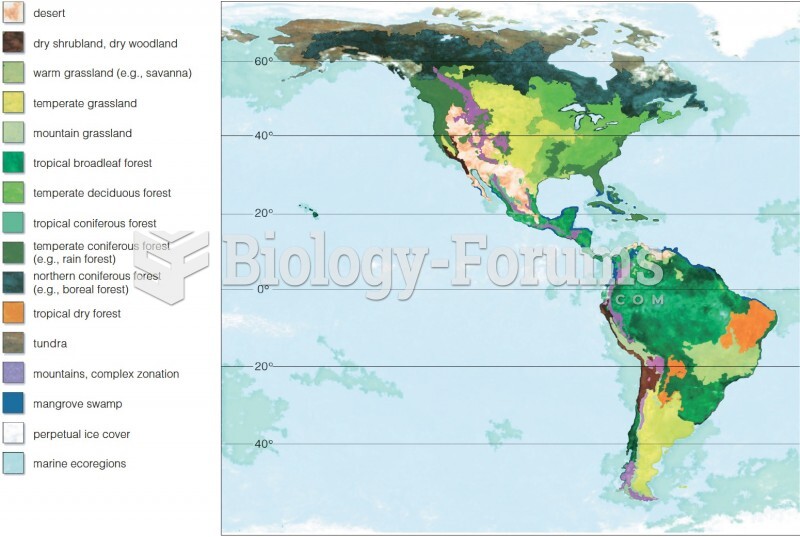
|
|
|
The types of cancer that alpha interferons are used to treat include hairy cell leukemia, melanoma, follicular non-Hodgkin's lymphoma, and AIDS-related Kaposi's sarcoma.
Certain chemicals, after ingestion, can be converted by the body into cyanide. Most of these chemicals have been removed from the market, but some old nail polish remover, solvents, and plastics manufacturing solutions can contain these substances.
HIV testing reach is still limited. An estimated 40% of people with HIV (more than 14 million) remain undiagnosed and do not know their infection status.
Adult head lice are gray, about ? inch long, and often have a tiny dot on their backs. A female can lay between 50 and 150 eggs within the several weeks that she is alive. They feed on human blood.
Chronic necrotizing aspergillosis has a slowly progressive process that, unlike invasive aspergillosis, does not spread to other organ systems or the blood vessels. It most often affects middle-aged and elderly individuals, spreading to surrounding tissue in the lungs. The disease often does not respond to conventionally successful treatments, and requires individualized therapies in order to keep it from becoming life-threatening.