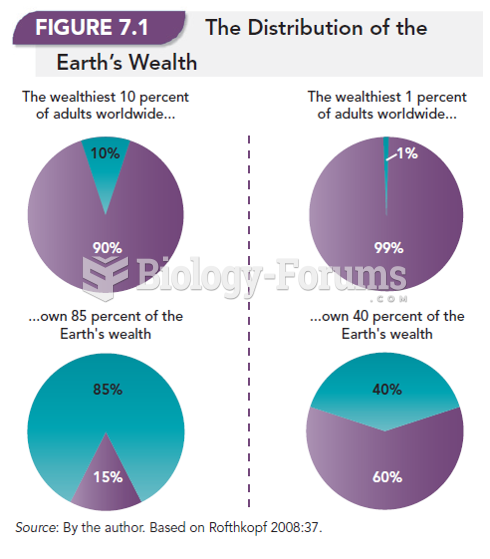
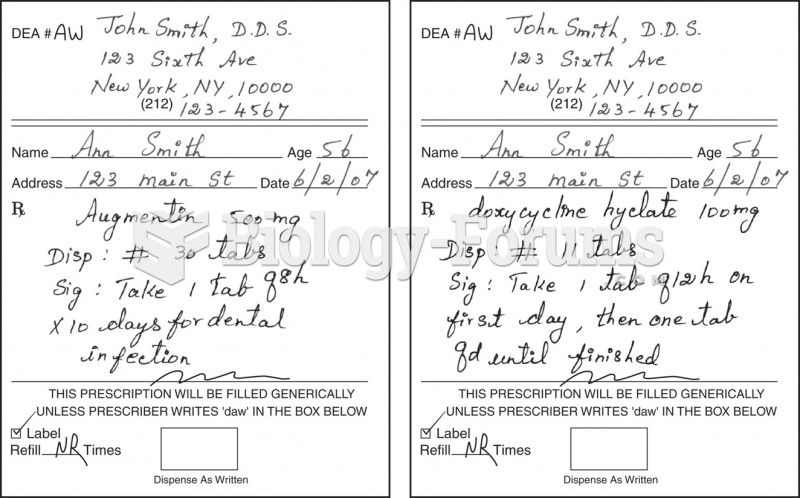
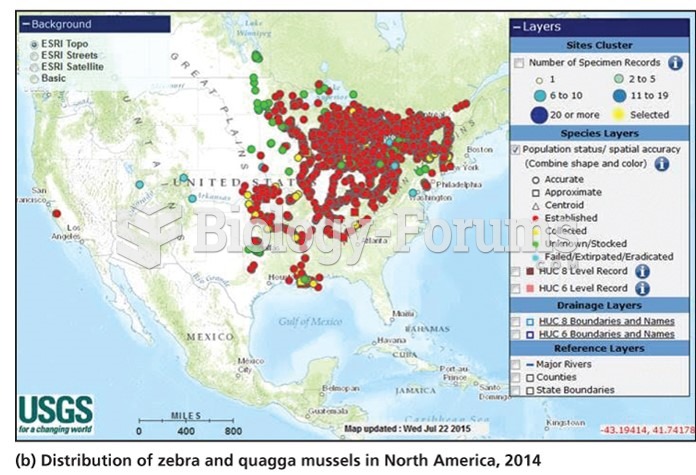
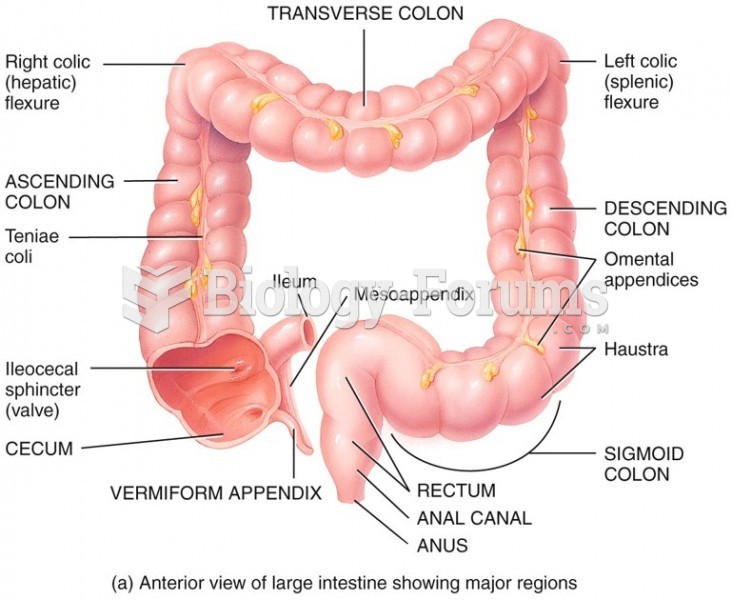
|
|
|
Less than one of every three adults with high LDL cholesterol has the condition under control. Only 48.1% with the condition are being treated for it.
More than nineteen million Americans carry the factor V gene that causes blood clots, pulmonary embolism, and heart disease.
More than one-third of adult Americans are obese. Diseases that kill the largest number of people annually, such as heart disease, cancer, diabetes, stroke, and hypertension, can be attributed to diet.
There are major differences in the metabolism of morphine and the illegal drug heroin. Morphine mostly produces its CNS effects through m-receptors, and at k- and d-receptors. Heroin has a slight affinity for opiate receptors. Most of its actions are due to metabolism to active metabolites (6-acetylmorphine, morphine, and morphine-6-glucuronide).
Most childhood vaccines are 90–99% effective in preventing disease. Side effects are rarely serious.