- Grade 11 and 12 Mathematics (Moderator: geoffrey)
|
|
|
- Grade 11 and 12 Mathematics (Moderator: geoffrey)
The people with the highest levels of LDL are Mexican American males and non-Hispanic black females.
A recent study has found that following a diet rich in berries may slow down the aging process of the brain. This diet apparently helps to keep dopamine levels much higher than are seen in normal individuals who do not eat berries as a regular part of their diet as they enter their later years.
Medication errors are more common among seriously ill patients than with those with minor conditions.
The first monoclonal antibodies were made exclusively from mouse cells. Some are now fully human, which means they are likely to be safer and may be more effective than older monoclonal antibodies.
Despite claims by manufacturers, the supplement known as Ginkgo biloba was shown in a study of more than 3,000 participants to be ineffective in reducing development of dementia and Alzheimer’s disease in older people.
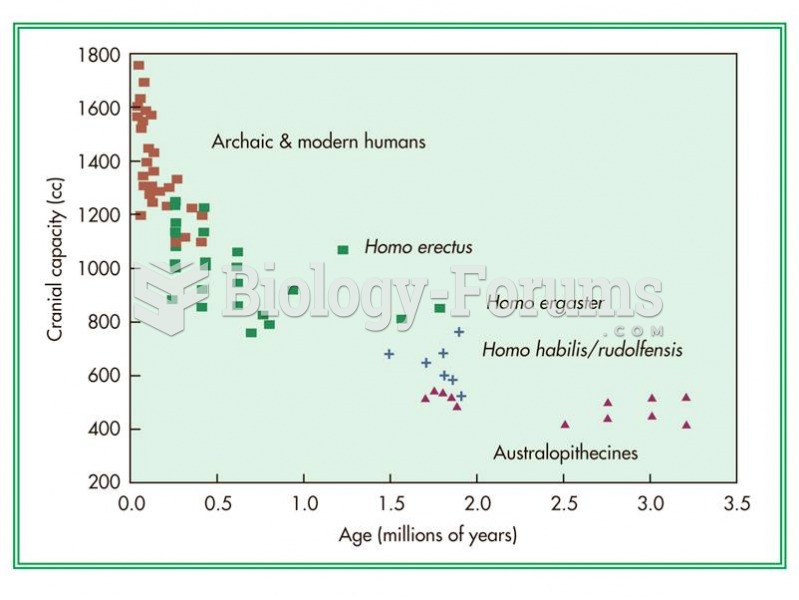 Cranial capacity has increased approximately fourfold over the last 3.5 million years of hominin evo
Cranial capacity has increased approximately fourfold over the last 3.5 million years of hominin evo
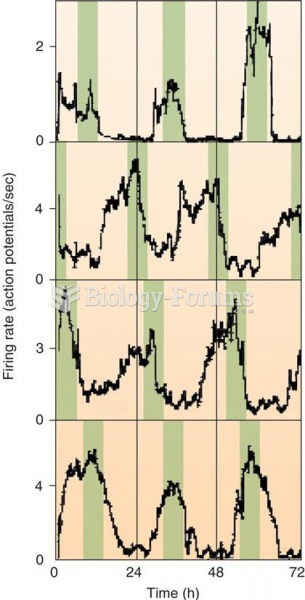 Firing Rate of Individual SCN Neurons in a Tissue Culture Color bars have been added to emphasize th
Firing Rate of Individual SCN Neurons in a Tissue Culture Color bars have been added to emphasize th