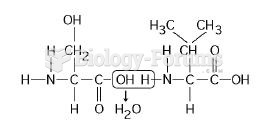
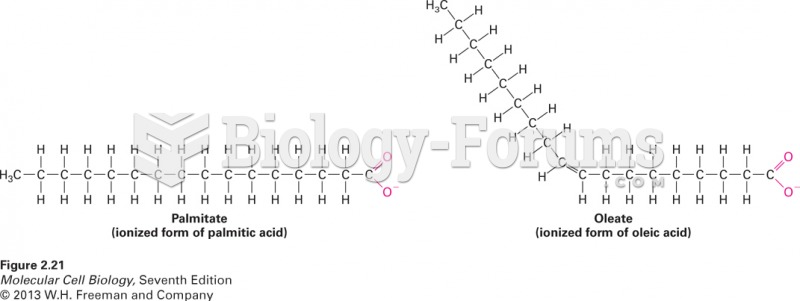
What is the best description of bond length?
1.a distance between nuclei that yields the best orbital overlap
2.a distance between nuclei that yields the smallest nuclear-nuclear repulsion
3.a distance between nuclei that yields the smallest electron-electron repulsion
4.a distance between nuclei that yields the largest electron-nuclei attraction
5.a distance between nuclei that is a compromise of all electrostatic interactions
Question 2What kind of orbital and with how many nodal planes is shown in the picture below?
 Question 3
Question 3CVeu11UfRwMFXvDIcT6fDFK41HE82GY20021JnTRUU17hnlss67RFKZEuwy4IdIl8Z/fAfgLNAzr7N8MllVVD+k8ZrutB+tam9SlP1s7FdUaudsnbqHd26dU+lNfbDlhbhqRlssfWyof6bzEoajhZ6/oIIlL76ZxOVKg212htalGsaYqyx4YXJitAD0lVUmZfVbXfV7LbcZkzjON1A9VnpiQNRI9nHAAAgAElEQVQk6psEKuwbwop0dtbX6emZtSX1WlP96cAKfQTsx08f69XhoSk3SXEYD8aNFF92zELv7DQImE5C8zGfjr06Ttstjw1hVIH8ZZ2e9kxsIGcYqxAgr2z31Gh07AZrT0ITCA+8yV5wyCu45yfFY1rzX4vI3xOJocKBgPjq+gdvLIwSAwMIEy1LlENb8LmtNMK3FB5xGtEeABskAhiE7Rz3TsNjTsS9je1s7vRKwrsMwayh2WCq/smJXj55rHoJX4OahoOZU9GenA717PEz9Y57OkKoGw2NvJW51O+deXBrUH34U086BK9A2iQv+T4CJ2pA9KFQgioZ4UcESdZ10N3QfrOtBr4Ro4lKGmjw8pVGr4610e445BxKjEO3Fc8BHbNbL4+kJ48f6eOPP9En//rM/UWnDis0HBMSBg7hZVe2VI/9EMSvTMnbAGWPqA5UK6jz+Jvjg2AhCfaDiGX2Pq7q5ORMT58+09rahq5s76i1gDWa6dmzx9bgQIk3N9pa3+iotICATKyrh2+3s5GbjyYE4QzvbOAUjlAEqtr3pEJAcThctRoN5yM5O5s4mOCsd6bNzQhGgNAHdgCMjJpxzEQwgel/dPgWJLaEY1XUeYLOkMbS4yOShZEgE/25ppORfY7J40UoCloADBmtBgLbWP3e0NSY+BMyOzqeC6oymqjfQ12FhD+x8h0eGCABBNiAIef4N0wmOnz5UmWctecVnZ2M9fDhUxtDnjx4qhfPnjsRhw0Q6DinU02OD1Vttmwty523ptUpB2Lu2NBBV/BiI2kJqQG8KtQ0H4zUrZW1XWuog++L2zLT6Kyvh599ptPBUP+5t6NGl4mVxiKZhZkgp6cj/b//z9/s6ff46ROd9s/UXutqd+e6NrcIcD0yWxTZzyu2KKL/nU0rmlUrOnx1pqMeyBPR1OTSIGp4NmEMglqaNVqEgelfn3+lXm/oANx7793T7jt7pHRIrrEQ5Qh4GI+GKqG/b9djwsLCpVWJG8g5TlhTIQeFpRSdHJ+Z4luVuih7BSBq3r7ho74mh0d6yaTeGqtTaXv8YvUFNCAvGo6kuSFJpan0CmgZzb8No/M4Lt+LzaLzJSRhIZYQ60mdwQbGMfS/mk/ML+Kq6CnKmkbzJkMNT4714uuHrE86OxpofWNN47OBMBJjiQtDQkOTMV5SpDGCA8X1EcXV2A7XeEjZ3wDHmWo49iBgkKETKRxhh0H//OPPdfz8RIPjgY5fnurVyyOVcbQhuyfK9bOBFrRVc22VZ6qSntbZt8jLFuwQfDllA0iyCnEOpYEi1e3iGZavtXpN9/av6b2D6+pCneaYuEum0j1MtqeH3kaNwFeV8e6DgoVOF7XF6fHUmZSevHhptVijtWbDQK3W0tW92xr2v9Sw98qulptr62o0KxoPBpqOFhqSbHBaEonqoIwMN1k4Z3OscJjyiHopmxAw2VmxYMuePDvSYPShHj19qc29TW1ttbUo9e0h2G7UbLrHz6lVq6oG44C6Dt8UIxjmTOL2wvFhOiu5DTP0vkwaK4zwy8Zxf+xJadNytaKz/pn++s/Pddhr6Pa9d7V3bcOsHitctTJTrYK7ZThmIXdgh7IVBWQyb05ymIj7oz8rqpDxM47fQOLzj5kLDAAJN0JLYAcDbqOGAIqUzS/rRGcTHT57pn998olOXr0S6lS3DX6NTJQqOz5tOi3bH5WGl+cIIIx3uEzyFmzKrBJhNPg2MJk8bPg84FRGzBjJW/oDPXv8VA8+/lK95ycivRtqKPhDDAGE4wAsqClRtvaRWCD8VVWGwiZVIEjLDzPzYhSZ3hvEg0F5ygsNZmNnJN9odbW7vq71RtvbsRLdwMSvlWuq2x9jJk3Hjj0UeYzpPTzFtKL5QDp8eagXL19aU+AUXPVmaB1KNW1t7ul4o69Rj9SqGHyqThdLEC6CbXlRd7Al7I21bvYBYgDyAEceDfuzoNFIeeVIWzB52dNRb6TZv77Q9pWWNjYqqtdG5n9RbWJEwiTe652qWmo7iACYYORAdmig501WWbM7pFqIWRSEbj6zeyzh/zjFq9zRZL7QqxeHev7iYz0/nOmP/+v32trG96Ks2cQx0qp5khOC47gn8/pQHzNwtqziL5Koczp4oAr/fQsSg5yhVA//g3QNAsfaHowk50je44l6R8f67JNP9Zc//Vm9k1PVQALPIj6JSIcqA1ebWT+KiXU2A2lRxMwduk/7Yk4sHAaPtcu+Ag4nmdq7bTZkvSwLx/qtdlen7a4mlTMj55XNHR2jNiLIFMGECUAbCadBwwFlhPqbClM2aWDDFRABE/0sOlaSwTBQdqKZTOwSur+75015as2GtSqES1mHa4efsoNWp+wEj3TJDE6AR62ICfjV0ZEToWR/BuojWgVpf3t7W6PBSGenZ3rxdKDj41N7woGi+Howecejqb3PaC/GGeACy5ZVeawoYLj9I9L+eqjlPPGHYyfqG437Gg4q2ttvqb3eUgP/E+IQgT8sBCl+qw1Vq42UbBu1WzN5+UUiFaTJcpl0XoFNDmNyxiSMGjVcG92m8Xiq3smhjk8/RnTQb35zX3fubDnPMpIkspLdsyiHwlg+jcJBjU1EnZgyVVRA3nz6RiQG6UAC9JL+ee1IG3xACuxQg4Khqlm/r0dffqUvPvtMX33xhXqHR3aCqVerkTQ5ZUG0cr5cUqvVta6RxNNMCCKF7XuAZxmaRfvCVrRISUZY7uApZ6OJxmdDLUZSZV5Vc1HVO1f21LpVUWNY1rMnz/Xq6TNL41A6Zridg+zNlrJKQm0ZbPgyryhJqmOBQRtQLht5cGwizwKsFL4Qu7u7unHjhja3t408uGwCIwbeTt1oLwYDU7P1KT67VpqH+g4+shzBnmhcWs2WCcB4Mnb+NnS8zWZbu3u7lvJJP0AcHrBp1xuRERLhl6hsNBHWpkC9iLsD+aC8dBcqHRufo+VhgjbJogSazhdeLYbjU7wrVRKGDXI/DMw+IDRDlQnynaumRmNNrXbXel505sDDVLI0d+oudOP4X8TCTIRPTRW7nFY0G+McBDwJYmhrNqvqw4++sFao17uvX7x3VRvrROKARgQ1hO7Z2q20vIciIy31EKFMETL2puMbkbj4Lsg8Y9NykIvlgl+yHM1GYz34/Cv96X//b335r8/sjriNKXjOshih4mbZSnOnQhqMRxZmMHPORiTzGFmvaVMnvGkZ5xCpNEbthpMOaI2r5cxaiXl/ovkAVRdAb2ijvakrN7pqjMuang718MED1TY2nDY/98HSr3EWDEADgFdxgIXQGBCVH0uo81rM59ZkgEQ721ccgUEUBnv8Ya0ipW1eWYAJvC+8pAUtRs9qOTNGYcb2YoPqqW/TNZYwekWfYY3QCtTqcwegHhxc93JLBPfxIXkvJhrPyBNBIhg4reCzg1WJ4E0orWEMurLVAVvGmujE8/mUmESiv7GKdtTp1FWvdzWzXBNO7xU0MfOZTllJSnWtr++p092yp483BmdQrIYkwybELDz+gBGUeDqEMhMCVlJ/ONbR4VT9Ppn8m2o1tjQYzfTZJ88sEJ713tdvfn1TW1uENTUjINUO94ASNSejA+Lyy8csFqbb6fBGJDYBZzqYRUVbEHyLKb47IQ17Z/rkww/15//+k559/bWdbFrVunlJwoQIIMXyhiUL3o3BAkjkPFOjaUeY4YjcbSF4qUpDgw+bDW2vil2WQIUJTm4zLUYLLfoTaTKzv2uzWdI66WYxrU6l7c6anjx54twIZK+x+TQt944zIwfcgujfiFIAgcmOww9DCwPF9rYIdBsbG7p7567u3b3rcwbMm8fMGMBQHRkuwAbkUcmJFykrD0SmIeQdOzo+1MnpiTUk6G3R3EAMoEDAgGaQrO
Question 4/gxjtaX1/TF599rsePHmk67dkU70R+FVIhUAMDHZSK6mGbGCx4YZyD8F+Zke9sSCovAmwXWlvf0NWrezo4WFe7OdV08tIBsTU88yos78A+9uiAtyYXRomI7OlEo9OeYwrRKCDYMSHKZgVJDDi3Dt3ea0JXXdZowopQU3lW03hKrGP4bTx+fKr/e/hX9U5P9If/uKcbB2tazKHKpGZgOUEO83AsI51XiBz3i/+/EYkR3c/p77hefr3QqydP9eWXX+ifH/5dD7/40q6Fm90185uzER5VJbWqDQ2rDZ3N8T+IpfCs1/cyeUIIPbFfczLYyMlSeMf5cuHPEGZQzRHZABUeTjU9G2raG6o+krq1prYaHTXRn570VZ8v9M7eVW22u/q83RZO3j1SJJHvlrxuSVVkHnJRCoRNgaPwvVD8cgPTqpxR8mD/qinw9evXtbWxYViM2NYWDILKmVgE9ZUmzmPWqNW8ayiWPVgi4fidoIZTEJQY3XepVhfReoTq0B7CoXgOsoGK690NrbfX2GHM44d+m1hCvN+YlAikXhEjNCaoMHrccsUCFes0ZVEmbEJ3vatWZ037+7e0f3VP6x0cm55rPIHqQgmREcL5yNl/qvVEcHpmrwbjvsYz4Dgw2wrLhQnEBI08FihHvLn4VKMRSIwumWTsHc1LrFxlTSa4BGxqvqjq+PhYf/7rp3aEGv7+ng6ubnkjopiMEQgSq6dn6+s4CWPjm5E4I6z5RwhGLFPY609fvdKf//IXfQ77METn23QuBxzM4cuqRkCpAa9XrZstQJ8PRZ5iopykBNvwxAgo9bKqLCcslSTnQ4dYLjuDIqzlfDAxq7Doj1QaTLVe6+hKe12bra6VANMhWTVL2sD/tdUU6qmXJ6/0+NkTPXn+RMdHh+Zv8edFyGO1gOI6ftQR0qE7Xet0nEFymwR8e/va3d1xSD2U2by1mYCQQcBNeGiH2rjjkRfu9ORE035f5VYnEJ5vWM0UPiNkEQKxXZ7ZEtgK7uC2ad9QVCxq1Jp65+ZNdbtdHb060qtXr3QIe8HEd+qDuQi0zD+bybEUkr+MdpVL5qXXNja0s7Ojzc1drW/tqtNpazGHOleNaKVSy4QEi6o9C9EKzWZ6dXyks1HfhGS+GGtRxpcliFGlVFFtXhWOQnj4wWmQ82ownOmsT6orhGUyyBPiT+AD7Mu6kZZ8JNVmVYPhoT78x5c6PD7Wf/7xV3rv7oG1MKQisagEE7CS7wpsRe5xHL8diaGeRD/gnZaSVz9+8FB/+u//1mf/+ljDfl8NUs5X6jYgwBdWCQdCEzErieQgnTqeY1KfcB+iHdg8ZRpukdxnOYdyY7VajJGOiUebeLBgRwbThcaHfc1OBuqU69rtrGurva4a5tvjnq1rdZwVYQ+8opY1q5S1s7npJfnGO9d1cnKoo+MjnRwdaURK1HHaAmGBrzI8Ytd7lOzsXLEAd2Vr21oJ2B8QGBSkfCYyGRyhhBBaEJHEIUxEVFnwhoOzUNE1my1L/FBecqSxTBNexeQ032eBGaf1WOEsSHu1wtFpoFF1om6zo4N3bmp7Z0/7pz29fP5KR0fHOj49FVHKE0R+lseQgmJTGDvlR2Q5KV1xf+12us7Ug3/FkFXSvtQdNZqbIQ/A186HmqD3LqMVmml0eqTF6cx8ODIywQBeNfG4q9RsvMLayu5JMzInTdi5ilWFgICuytWu+V0EyMUicrlVqi17yTFQi3JLw+lAT56f6sOPHmgyKuvmO9s62EPzE4tdMFqRPtYJ2c7jr6++HYmT9K061qO5Hj98qD//+c/67F+fCV+GusP2Q4cLVUNdQqEACd4G7WKzGlEORMxWpiMNp2P7URCezhpvxT2Rs87sGLphJ7IrEWLeN/swOe6rNpHWuqiE+GtaM2EmkpUiBYFG5EBJLRJMV+pO19Rpt7S9sa7J1QM7q+NogYcXTWT8Ea6gLLACZJ6HDeh7D2aii9kEJ5nU3acwj8c6uoKo8ShdIgQ7DMn6bVfjJ6SYhSWIiqGg/CXmL9EZL6FWn9E+fCbmJgh4sLXaa9q/hipuR7h+jsYjU2QmDqo1jmTVdJJEnH8aNdUbTZv9mVCoKk96KRsoa0EZp/c1p+8lK9J8caL5rKc5OZ9xP0X7RM7n6Vyj+VTEQ3rykiwy6aBLJFkP7aVGyCuLrlRumo1YlDCq4OeC9MA6EysXgjXjO52VNR0vvHnlJx+TNOZUvZN7qldua3cH9WEMK4QuzdEVwAtn347EvAx1WCz06vlzI/CHH36o3ump2viaIkCgZUP3yqtQwmTCpXdI+q1qRc0SWwnUVRniyLKILPMYBeZB0egYmxyGqo34i3B8Yd88jWfOn7veaml//Yp21rbVqTRUZQ1DQ8dKYQ0GTYW5RDiKNK7e7MbRFRU1203ViQJBnWN+P6ntpjNT1znlQZFwwbTJORKnuE8GGgMRGXW4TNxaepIIolXmRFlg9CCTCJoEcy52XhqT8yF9SbkMUJQUIwWcWZkJwmWFmg+GdmRCL8ycILdDu9FWt5vwH20AFkyQWDNncrdgTy3ezJJRQXDFyikHdILw9A+HJnha2AGurYFiArpd4VvCyrMokSlo4RD7rJ/GjsOExDXAESxEsczJlVxXvdFVqdIxr71QeNyZ5UAyB+ET20QuC8aWjKbHpyONR69UKTXUbXbVrO+JfRcBN+aBECuKEDfY/d+/h8RlIpQHztT48ccf232wWW+YcmFdrSBQ2OkbxxVGLACBhImEjvcVLIJ9EqoLNRZSH+YepxUEmaTAx4RLRAOUkSQdzF4Qf63W1nZ3XVutdW01u+pWGqqgU8ILzUt8ihAxPsydo4JOO9dEQm4bOnBkZwAJzGEQnX83jAYMtREF2T4iyINg2kASwGPRd4xZQrsVNxqToUgtQMak87LDEwyJt19wBkwofHyTh4U2YYTBB7mKhc+8Zjgf0eZQlIUTPQ4+WMUyexPn6InhR4eao8fFOYgyIC0kzWZ+mkfG8BHBBeUSuZHJn1O1oz3mJqK/QzFIW6YqV8i1TJhV6MwxNYNR0zH7fcB7w0ricNRQq7WhWnVT1cq6SuVOsBDUn9wS0PnT35Jz1+FLk7KLkivauo6ZXj7v6aOP/iVyU7/37pbaLc9yj0VM+BXy5rM3InEMBHrbiveGePTwoR2omw0QuG49JLtpmgJjZ/cMj+UWjyee4AjuxYRlGe1AuapWvaNOtak6KVPYHWkCe4Gsjt9E2su5jAM4ptGG1podbbfWtdHsql1qqMqAWEtOHclRG59bpzUlkcfMaUqhIpUaUSQQ2DDcWPMxj41nYBVoJ6THulWbQJk6BPsRioQKisTZ0EaEDLLhJxYkQ/DCEeQEMaibNz1oBabBmXrCYfXCl3EJL8hkQPNAIpOKpVqoZGI8plgWGVjyvS2cgBHzkD3aSrIbK49tdDbvHU74oWVCxYlFkq+BM/ptQrTIzxwsHxWV8Ws2FSAT/8TLPhpQGzdsKKpqNmGpYEvelhq1lprNjlqdLZXLHZVKHc0X8MEk/0ZQZ8aSmBB40OaI2YPEYoyZl+pOiINP+NnJSz14+ETddk1bGy3duNEKakx7kjXvIuDeiMR+2R9KvZMTIzBI0N7s2MQ8HZPFvWEAQ6VMjZMaziGXUEnWRUYAXwZSxPp5Wc1aVWvbrTCITMd2VJksJkZAlEwo60lyR//rpapalbraZfhgfBkghZHLgI7FvyBtbkey+EGxGDEPcprGGDlC84XzSuzO6fWTihJymdaYrDLQZTuoAwtWkkDhi2BM1yarpRRgSWI8fKWDstvfgGvKyCTcxS15CiMvWgGMH2TZhBWDV7e+2VZN9pGuR+gRtGsefteMCX+oNAkGBSaENQE8JoWTIZLvgZi4ajNmA5jMvnETnKxIKAPkmqrXN418vDtBpTYZWfePro9s+p6YBBsyPuWWty8gOz0OTOTbg2rPSG4zx5gTLBBpXCGlCLSAmdUWVSHCIHKSV+M5rq6oBMsaD6d69Oipnly/qmtXQ2Mh+HFPAQP53AC8EYmplN9kMLRvMHwwqhv786LQ7vU1mbPvM8WzAiKkhTAXdIgBy652LJcMKLrnaAN8K1lyLP7aVS
Question 5ZMxNjTSVKMW5/N3sTVwVrg14vvw5L/xTqUkoA42DTKr6KpCF7G7fUkshCXDBx2k4AywxsC3NCHo5M2/wrlZfTpk+PvosFQM88F2mAmjfu8FxTXjAoum+RNrocRg6XcDvdMAlgqXChtWv/mdKBulmZWIPOgbkPoYhkJ+1+MR5qX2RIMV0/43vDzpa0s9aje0BZ44qIBSKwPkhTth3qzelG7+egpQm2YzYmIwQmL/B8YLcZoK6ZsUM/bxNtFbB9uoWXyPCPA4SdB2wjdWtQ0w0V2xk6xEZ6P7zK8Myo62JfI94FWJ9rmGYXxxCBfqNnuql6e6ejkUE+ev9RsdlX1JitGUHHzFa6R/2Jclkic8dshYFl2sWZCVt4/evBQ0+FITWYz/ChmUHwMkgAVLEUgA8Ay9WAQrIi1lOKGeLhdNylDQ+doAge/lgTEGtLsZK4SnlwmKF7g4SEshCCYgKOeYyCxM+DEEhnOJIFslEv7qnTKPKpJeBBex4/FJt+0F6mbCcMkDZ4xdLvZOSUjA8VwDw+6ksOEKt64pdQoa1RZqM+ecq2KpiCDgczOw6xGsRoSZcxyHdQVaACMuEY/DgUmOWLZGg7wFF12eBCyHOP+Q+pazMUQGVxSyYnGgLLojUcjW7k8MQFAMhgZWFajhUmcYXFYVj0RFWcSAknrmpFzuUI+kJmw5DUgU9b58i4TnzaDOvhZRAQ4mo9YtYJ7xzWT6U2fYqU0qtvXwoQBn41MIJjYBmxZUyLgMdhM6np63NPL3lgHG+R79jQKcsHKvsLhQkLBQGo/IyGdV1daiP6zP7RzD843TTLIkK0czyuym1dZPhLlsqyF11gUZodn4MiAMJncUSRiECQog9sCQHMeCA9HDHoJN0euQeQQUczLwSVANT0TmaF+nnmmsPLZI8sak7g2D5hChEwx3TUozqodNMPtMYWLc1NrljGA7EGhVvLuMkGhrDg4DVVqS8PKXANUU+0K7KJ/XkNiQbMBiEjhCitKCZ89VjBLv0FTEMAY/Ck5K+gP48AEJKgULQE8PpoLto+Feba0Yb421Fg4a4UjEEhMi/nf8oAncfIGtHtowBAoAg/cXZnMdmPlfBZZ6EPTAV8bXCH6Ga9YlAzlZ2J41Qsa6ffBMaKw4Z+T5yIrM1oU4IkmC0SldbBEWAhRD2LeHpBs3VbGhl6cDfTgxUBbV1uOtkZBELHFAVAr7VK0SUD7wv90CDhi4UK1Ru4GfAZwfhmPxqE/jeQLYZr2UsvSHtTMLIHBWCgY9m95uTqLu0GTjJpJcg86xf38jG/Sn4UxkIGXQeT0dp5AgRb+HwROKG8hlEGIe9yNX/Q3JkRin6MmBi//+dVUEvWwYiVkYvmmz+Bce61jw5A/hBDww5cd/+YEs7yY+oFfyH2LSRtUJN8zL5Te4svk0pcmlSeln67gm2pNd9PBlKlQJuhr+EGVY9LAniBwxeQyE4dZxBMudF3wuiAgiM27od2J71NwBKjjpTLLEbldK5rs9lmjFe0xPCBu/i4cqnoQz8cvdNYHwUNNaVpiuSoGBePZkp0439u4Yml99fKlvnzwQP3BQOsEKTabtkjBn5mHovREpTKGcglKuebLCk73MnXL3wfgwfTgn3PXVwNdKMzIGgiVETQfeQuk9B8IzLkxMZWdBj9TYZ4v21KogtPlZy40kJH28I0pC42mYnNYM+9HTM4MOxKZ+nl7IZfqjD3WWlyo5Ee7DKocq1hUynQGf00CvJjRmeiPQQw6J0oLvvs0HhiRs5TqrkJ50Uh5ewwzE0n7A8WFVw8hNmAdWiFPQG4z2UmPFaTfWqxB/1SPHn2t3ul1ba+h8QhUy9Vbs+Rg3mjypf/De754/lxfP3rkQWH3HgtnyUmHbVlxcKF02ANmhPmcZEZdIeGlxX/vm0bOi8jqWfpNJPYSCBAZH7M18U5GZIBcLC88wqKJphUZWWN8PUFZShEA/dyed2TgjA1Toh4GKnTCRnQPe+Itouif5H/aCzzcX0/ImIcgB/f8S+fL94zo7vYSTu4bGpfEsrAoGbb0mXK8KgfirTrq2lcz39ALhDfxgsgTIFGGhZI31Xx1ONTNg05hW4PUROqIHUVXxV88w8eBFPzHJ8eOO4P3xUmcCFcGH19g+0lbpeVpbODEpuXo2FPjLhacrjPAEtjyOC+P7t9rv33NA8CTBoIj/4yoXhhyTdAPJl4ayDxwry/S/CntgTK7Vx6jSBYD/8k94MPG6aZclFWsMwl25F/7n/yoz81j7N/WD+wo9J3ygYyPBVgAn9yXi+8E7GDK+BVkBuveY2UzzbCcFLDmzTQi6Syt1paRQHbWBViZ0OmjfpuMx3oKS3FnS+tt2JeYFBBT+45aQnkDYMhdgC/reDy2PwFH+/2SWzbpPL00FDrumchCC394EQvNf7290SgiYfHcwEptyvcZDP9lN0Z02PwlwS6/F0OS2AgAlv+CQKyuWY0s7UeY05In9ha9WMtw9k6Thi6j765X1O60AuKXgMGvrebZcmTyq5c8Wr7zXU+MnAmhbVI+h9xR4xI2qQH5mwxTR+EkOHLPkdEJzsyMFR5QwGW9QNDLKxSR3eQfYaeAukPXvvrqoV48P0H29884BoGEv8C35E2dJwHGg4cPPQDodGm893WbofvDE4qZivoFihZFUQEUCZu6EfxNFXyPZzGj31xABn4+GuhJK0Kb81JZLIV3i3AGblBZ+zLkc3ASO4qFjcgBYUoMawGMEN6CeYzlNUHfYUmtyPyT62RIX4e8+Z23efSY0Mfiz9T+fL8zzPIx01DDxyzI+VXsPDEIlWF8e6GiInALj6LcuAH+DIeoXwmULenx4yd68eJQ4/FqOoeoH7uNVosfo1nIiAdyDodD/+EPzA++EZfCMC+z031kqPFA2wAQRaNSA8m8zOA4kky73KGMzLwXYekOe0kLzzEYIhMyr0mAkLU8LXlc2YIV8XBQPFORC/M8BoCHUBIAACAASURBVIxvViif+7fsN8sfineO/MvCDXrjhGAsXeH4Q1+C77cz/2Lh+LWzKZuKs8cf+dIqTkBtXtnv4oIYBhUGes1eLQB/am8zUyr03gh8ZlWwsuXBKozy2zxFcM4rU9LVWrjzkKW6L+A51RuOZkOTXj0RrpiGELjID4dBBXjyvnlbwjEt2GGxw00XnTzA4S9wzhyOPdsgB+zjXbO+fDQuazSaOSWZy/TYp4GBjU0OaAbPiuQHc85NuuPoBPMhNKyAJVYtBWS5bSQwP5SAEI++w/8BPRPEtLRdVogRztJqIHc07ptvFtvFOb9z9xICu7Ppcyv1rPwP3pmgzLAMgsyhlrJ+1Ap9VGvwxmw+SRbIjlMSgJDuSUHzwURDc4HvCb+MFNTNoIK8lPOj/C4Zq3NwSc/zvYyol7VtSRAuwHbVxyToLSeGMaaATIHMvE99rOphCUS4g6rjIRdk0WUadpmJCIXCZe3yPQS4CIq0x0hi8qGC4frncLhLv84V0OrCoEDmlqN76Yf//k0G3pa6JESk84sFABSoQEKp5WNbrBKbkAeKY/xi9Vhd5bv4IcQAcKRUdvrEMZ79adjfYn1jw9l1EDpI6g0V99iZKpecMZ5NwwejUyOxJwwroLUcvGTVwbKdnPj785A89/w7XaRl0H1flm2qYE6oWGa8E+m1ivcvnhfhuCz33GQwll6gN8AzqC+EiYmOrhoibbZ3hoccMgYCX0DCBC5VzuSvUpl/GVKFloHA6IX7417wv3jenGtUJjeFj37M0yI1MUFerSdQhwzIy5DYyxkwxbJFOfwD4eHpjaCBpAaxKW1WpSFPRN4z/CCCMocelFWru74mclIsfxm+IHm5rI31DWeTfPHy1HUGX76a6m738uNkOU1DVLj9vU/dV09uk7VAYxuBQB4qhOVIRgvXFrD1E+N6wIxHuXmGYxE/eJauKRPtQ+APRA7/k/xloTvWiIRHopUDwI1giuSjsXyTTxPOLpG4WFxeHkBiqEb/tOdvIfNGiKIjT6GwZQU/wkmAMHHeAOo1lJj2BkLH8k3TfJ0GMChh8MIZ4MtjGoSMtHQVnCTMCPjBPkBB2f+D/TsYdO/5nKxyBoMpMYNHvRKZ3IEp7SqjX7
Question 6d7W1JlUWjaj+6HBGHuH3X43LQwDExM6iCVaVIn+NEBs7FJxWhGK7F7mQXK5S6PufwCYgMHngfqEyEe/LlHMhEe46bzz/Ey6biaqtfqKeNmwMgLifnzb2EnQOL1tXW9ePLMVCOQIdDdPrPkT8MF8IeE+JvKTsDxKxcocQAqsM4Ik1pJH/jndlv9E61nIDLw4zz44aDMUN/od/YHgAJDifFhABHxpWAjGfLMhS9xanjm61kxK1K323TgJ09zG427gecr8vKmfn/HZ3SBOovjaKprAsD95KthCpngkbthJGYmYpMLmOWNw80lBqiXMDQsUx+j3qDwOE+5DZS7RBxgi4DHjVgNgSeUGscjklC2mm1HofNZ0hPE50TpZEDGEK2oFS8TBEgyaAYLHoVaoUosgSEVOjCGBz/6z4BJcDDAXkOJ/SyxCQxe/uX7mKOtKlsiUbxhuKxe902oP6yGM04kpLaWwm7LhMZXzS6ghQhKkxqIkIi/EFsNNCoOSjWiJw8zQAt7w7+lbjk39Ac6un/LXnESGMD98Ec5XzHdZeyDSgOY8FfxlybefB8ImmHrfhWIQ4wZkyNWpcBi3mK15NsEh+R/A+Eg/I09VmBrl6rk801TFZUH7nJWfHIs/Eh+0iY7Of683sLXilHPEFQgCC1uaEYm7PBJkDHSpymKHcbDH32nycFjUxcKVzP2GYt4ifeDRaBnAfB0zQRyC+BZ492gDGzCAs8e1MZS7fI8wBW1RiPC0y6oEh9BX8w2eLDsq2XqC0RME2Ajws7ntAKoGXF7Zi8RosymtKvREvu52VGGEfEvqJf7sEBIKanjLc5is3SiGUjlRQtYMXDaZ67xtVtqGHLGL/Iou7/cN+Vcol+CaxrLVD2w5xe+I2EfAA7xi8kWo5hQyjCDvQG+/MOGFmZqa09YUMxWepgCG4GFLWfJj9njGfPCiGlvNuqMsQyHfT5lTLmfHIrw1CPez/wzsx6FwlS1xly1RhhN3RdKyuIYenmoangt8YBQkegML+PX2mEWOIJ5oRZuh5WKU1HZ24kEGkZuIAZoV/8iZSfulzQSoCTAsdlK6j95hf1V2QlFDbiYxbSSwMaQR0lrlX88nwJa8n7xNVSO16mHPnuW4+8bAx69yUMZpYQwlrDEWoGgMK47vEKdgd2ujsAHSks0tvloJ89wlAkRUtNFVQOYxVZX69t7qnSIrGCbpcRmzYkrY7PwACzS91qn6wjwk15oKMwWs48yiVHI2Wb3yyB6GY3oJ6uff/TVoVJQr5SbDSusCUgKCWLye6sw7C7k8wiH9vgeeIKtMQE8REwiirWvbrAMfAd+LEkbWWWIFeQ/irARh5MQ0UKfzmod+5FE8EhMKvYBsajsecNZTB2ITbARFVVLkYSQbYfr1ZKabPZeHqvcGqnZDpLFEGT1NGDHbxm/uvglHEtXPkDiSSaCbnN4fOw4Lse08fGMvA2E2+CmZ/HIKGykMfVk0HLh0JCguFQD0Mi1wL1MRQPZeB8sDBgFpY8yckmec5E/037Lxm8LBMEKGeB+OfsZR48scKfOIQRCtVmBApTJad7LYnbrDCrhyAnTQPxmrZt3MADCHINeqZEjYaRSva722npKvngRmLQqIfGi7E1xmo2mk6GQzgv/atR0UD/Ul2Z7DCiQNpeVYGPCHvcAL2SD/gThJ9KDxoI48Q7tdACqV7cwJAX1S+UBE07d99BVA2NzDumexyvBLg5Ukr7zSdQVQnIMsFWGRjK0P4nIxFdummv3YDIBQAiUBlD8SCVWKY00mpLVf6hWp6ZaPSYw1HvFFkbDcRj9xs+4lyS/zc1N5yA7ef7CsV3wJVil4FcsMOEjwGKSpquXRaDi6IvgN6kgV5Ngu6wzX9OcPOPzu/ml/A7t4j1+MaE9t112ni/5eRrVtJiuvosy4jsjcF72M2tUqCNVlfHBhVA+jufeBB0/ASbxWGqmjQyBTa47f3/uWJLW1ureXuDh19Nw0SX+jaydqPtsvVu1N74FW4EOvU7EwdcrSMXA8iwmS0D8vBLLLM0Sguda9c2LxMYBHtgIyo+VCgikFSEPWLoGN/yOE3DnicU9XgxWgoooAdgH/KNqCBb7H7JtBX7XwIE9skvtiXeUYlctfisEXp3H+pD7zZIUZbomwsc3tja1feWKU7aSQJkEI2S8Iekzm1O7YLMLiSmHCMTCEWEyqbwlIubyv8cRIDCJGELOOYKcy7ZTdkLOJZxTfVDuTH+9gqT3MkC5jLauEMTFFdoLJZsQpGmWhx2PiA1raWNzMwxCqczid2bTwMWytLZec3qs6iexDhliRl7Ys2KLOacduWf0Nv8CFZxnw+uZSXQCRMguvBkIFMs7CM7yG6VQbqrLMzuXF8IZT3AfYBG3oAfFd78KbciDmkqMbgcbY2Q2oYv33Y5MadyFXE4cqYPsQlBiYvGms6HG44HanYpIflNzdHDu++oIUr/WKZ5BRVJukt5pb9epWPvHx07KxxJoS96CbQmYpQEPt5Hz3D5OuU5DwZHB5Mew8Jr/uJf+uF72Nb0bXxQK4YaJfVSUP1++55P0LA7LR1zGJAu+DGTn+xigaI8bzVIKLqQ/BoiB5R5c7oRUpvOSRqyB1bK6G2vq4BfBi5fUuWwA2+02K7p2bVdrax3H86HU54cWyAlXii/7nAKNVvGERnhZ5TJMuvCu5i2z7pa2oobNgxOvBnCjwwVAR7H87yTkZiOg4sgV2dFnBaMl8ufBTZ9TlZE3I3wGhY8hd/Cq2Q4f48yCpgcGB3wS1xANDV8s7z671mmfo8Cr1sZZIDEFJIRJh0AkYFWvGYn3r13V56c9S+M1p/4MwQmf4dz4wOYYaKuu4CHTgLrcTPELrbgwPAmxE2LFWBXeXjbTqi4EGX4GQgJOtB9oJirD89SGYkEheQdCQ50zEmeFPqUWP2O8uObPvhLsGKSFRrOpaq26tra31eiSMCTk9GJdxjm+TcDF1+fatW1d2dlKEb3kcw3Bi9UPHjeY22Ip0ZHcTugP73njRFcQzveWCdPyb+kfaZcARyAGsWawaEfm/1xF7mks+dRhXjvdXtbpCVFoU4J/HpWYjPFRfBNUPb7IdVysm/HxALgvCLmz6VCLWV87V7q6e/NA21trQfRo14U2UE9epwotK5xSb7mkje0tXTs4cG4v4shG06nDlciRAGSiwdHIABISD0JGCFdGgAIS8Cb3oHL5GSi3ukbwYrEv3uPdkKD9DUo7X3Mv1G8ci+dQ3Ev/scwVnnDOH2wB/3wd2rpA3IR8hl9qN2RiVilpjHTcbmp9e0uVJrt88O/1P55S3MZmTZub6857hrXP2huDjclzWQmGWppGQCvMtsZJpwWAmDDIia0AV9xgxPmwjMUUhOrzVywvzhnH5d/Su6xwr/g8wcr9zfcdHIrRIv8xcfJfLie81iAybEDD0e8j2HrzTbIeDcjyrL3ddd25dV07W21zAPDmgWsB39zWc+wEwD0PPq5Kqnc62tndFbuCPh8NNZ6wYV8w92VgZI1P9lRiDsd5RLDGrObtJRVIVG5ZF0tgzkfhm2BQoix0ksExrx3t88yzRB5lo7O1tTThTqbQGZVAen7WZKSJ4QmTKAnP4xX+j8lHn0AVAOUMBSC3jSbcDzSblhamxtvdrta34Id5P1VGhUaidEjRx9ymi5isr1zZDHURQp3dFSPiN7OqbrT/y5CiRdHGoKTcB2lTqYYJ70Sd8O78451gNWg3rU+N8JtRZLyXbkBc8ku5aj4BTq7L/+Xu5VICKun9QDYucgF8E21ZfrCqjlFxUpxSiW3feqqWRrqyva6Da1fUJu9E+l2OxNGe/M75pTfNtlKtqu39Pb1z+5aznA96PfPEzgVm5XfSRaZBAwIIKPbispYj0nVAbQIBA0HdqYTA1mXCfrg9CWM980I6BpEzDIKWBUAy1UJf7WXJ4Ahnm2Wn0kkMbwyGh7LYd1ecloY0+JRNufjHzhxOzx02RJw5Qd8QSlKvantvR5tXrlhqC0q4KtiTMyEAzYgJQFrbmq5d31N3raUB0eMkNnEaAFqZl+FczgoZeI+7hPy7LiMJd0DUcAkFUG5pil7JCIkQiEaJZ/ke7/qfzWGregwyB3
Question 74WoGh8yGPkZvphHvbzyBMTjjbFL+pxfVSz5PGij7QYVTrJBUuLofb21nX31nXt7bRMhZnY1OP+LyuMki9nJ9LkgfJgVqWU7vamU/Bvbm+ZUIwnExsb2Agb7ywKN9UiNdJsahdFms+gm4KZsmULTTQG8mk9rI9pmiO+Q5Yoz/2je+wenygj7c5sSAJPZkPSpdtH3dznL/8uXheHzO8nusH98GQrsEPpGWWQsGSkufqzkVprXW3t7arcqDFzQtGZKywcE0gD2Zj4FWl7e127e1e86XfkXwizvuFF+i2ERlPaNIHpiydz4b5Zg3TtnkdNMc58F88C4WkQz2E9LmMpCg3+TqeUnf+ot/iX+uD+5PaG01F0C8I10Xhw4jxsv/vNL/XuvatqkvrZbYkJ6B4k9oVzq3mjy6nFuf50CWJmZxb4vb1rV3Vld8c50qCcvE4OMJsJLUykmULS7ZR4mkQs/stVJP0zkQU5uiCfI9T4D2/9lDHdXlUJESM9UxE0geDGaqiPET8mA8unDSo2qiTJnVmRfCWgROnSoM6w9z1SpSa+GYQKypV4ZXjn8kKT0kLjxVwbV7YMF7tlzqfOo8b7Jpepz/kQsEakhP9baGtr3ftnoBclcZ8hCqW0sYKvYGGCci6R2YXlgcr1QKYCYVZEKj+zKc+8FIiMQSVbvFYIVyjP1SYqkRv+umMG4Lk2ZcQ1diREzuVnChzXrJz+g5Wweh1Z61hr3bru3j7Qepc8bXNvLjlPe6qAtMU/qjZPTJFL6l5osJErISqD1Flf17XrB3r+9JlOXx5qNp6oRA4uSsEsuiDLIcgZ4GHzQ0v7Hg6ocLwHoqIhZfMXrIKuBwROy4WbUJ6rRAZI6DD8sSl6NA6K77KYIIxfarP7sTznKn7QnOKSY0oH0ueljnrT6xyhthY2MLnaZyKQKSI8LACY8rZbdR3cfEdX9vdUYUclqsvm9Vx54VhsEe82GlXt7l7xhu1ng54qJPtzX2OCeWIFqUg9yCXQY85dY7LDgrTREYePETlcRvcKfJhWtDtt7+A2wdKlCbL0beBBhmah4en9i3fOX+e2FY+0CQoL9GlrHoXUbreJR+R/q3gs2+2m7ty9of39Dd/3d6Qv83YQ52vMV+cEuwBa6gdtYekkOfNsQoo+1dpt3bh1S8cvXumjoxPNZiM1q+yuEwCkaeQxc4wVgEv3M9IFIOlLJPbDtST4MXb6wU6/UqGYZ0t8Gr4EBi3aEH4Jzm4iCJd7wzEToAvIFDxgetE4EJs05k+z6GCWI+mEM0Gk/R5uHF3KJfVJRVsta+vKrq7s78c2EM7Oyf6Llu5ysT4W2xfoBC0G3yva2trQ5taGXh33PHG8e6tTXGVqaKhFectOuAMJkSk9/wFN4AMc4asjXpX2AzSewaPTFxA7uJUMsAJiGdlcUuqHv0znHAo98uzP76b7vpfa5KozAufvok6XGqgTe4HPhrp+bU+//uC+tjYazlTvYURgLdZZaAmnnhq5CReeeVmzzSZbS8plbe7u6uatW9pYX3coCZ5uZFUM0S0jMYIPbjqBcKk7bgZKeSpFyDM7kUK7M0thpxNHUAfienlMMMxLJYPAn3/p2bLteeyj6hg4zoPLWF5DYT22qXG01X/cN3HI2ojzR56x7wZ+xHv7+9rY3nSO4FHS2jgZ4bIx6eQCgD0kWCI01/bWpq5duyq2I2CZBA4OOCWpoNkqGk45tA6VZmrpElF4lmDBqQlH8V4GEMdAnjy/l7BNMFhSBz7/Tr/cjnzMhVy8LjQ5rbLj8ciL2J3bN3X92u5qcJxEMix5wCHwI6VfMJFb0fdc2+po2EXEAX7F/Gbs21uvG5G3d/dUrlU1Igmz94vgjfC0YhBIEmIvs+Aholx4VlAYBogYtIRZ5tE4p1GWqJG8UdMZ3Zcb/PGtv3FpMTiYFvgLehVHznH3C3fLeC9oT/E82hsDl95ndJdeW6l8sxer8jB01NjCdueK7r53X1u7+zEZohPGoWhLLn91THRyiWfk6cWkure7p1YdVoIBIWk4yatDYIZaOyeoI4QDHiumNtq4Qr7wPjNYgQiPPYGpmWSCJUv6ZPYPehw8aSB3QHE5H3LRLiFjeT6mcj3i1J6hn1pinE3UIEiD33E9Tr6OroD6pkKlVpqP1GiUdf1gV+/dv+6dRr1/NawpHpQ1MmiCTaa55zQUILUdgGKJYwDPzxjrZ93QhCggJLu3b6zr+v13dXR8qsNHz1Riy68Km3TjGEOjpFadXXXgyVKmx3JI9WxajdIa6b9mnCWyFV66arc/ez/5HYgO4GF5rhq58DqzY7YnMsbfVXvPwRxKnx5d6JLvQ4GhxNA0vuNV2Ah+LqdMpk/YDanWaAoqi8+wmLSzidRs6Mb9d3Vw+7ZzK5fmJedZRsAFcUJXDNUE6HF0hlDLAKEGsxBHyqtSSXfeeUef7O/r1YtP1Kx1VVNV/dHYrZk5RSm5gWum+ESkWO4ANmbBgtAwmDTR8IN1cP+BHvCjHe6lSgt2n4v9OOg/31gT4/dzxss0WRIB8gHLmCcZLzIuTADei1wbFIUc4RGjShNBVkx44hBWaTeOUmenRxqNz9Rp11SvlzTqn2p3f0t/+P1t3bq5ZRpHSRCy8ISPSegBcj1urC95hx3DfGH+Nb+Vjgx28FNB3dNcVa3V0sG9O94s+5+zv+v54yfmr1q1ppMlj4eDyCdrCY/yQ7XGUgt1xD6OASEbBqxL9QzFi4s9N6ZORG0LjfWyTCJAj/9uNK7o2smdTHVyF16HxEukhrKhJ0jsRyBxAA5gu21QZlLXjskBzD4aZY3nU3XWN7R744ZlBKyWZo1MJYwWbkLQRLqe+HkPOMMfdTAZOUfIvLqzqbs3b+nzTx9oOkRYHms+wi+x6lWGIEn2mtNibAtfLoMBTMWG8FsuRYpWjylvxdZtARP0jdRJ0hsQbxXkCkxCG8M3ICaTGjTlfEUe+IJUyDxB0AoykIRsf4TmA6pMHhBuxPpnNsmJ0snaM1G9trBDT2ne07g/ULdT0d1bm7p3b0edDjuPMp5Mh/ghCrFf3kpNmB6kw3nB7vyzc1fMdCdOxtmbqN2tTb33y19qNprr7Kyv3uGxt/UiuUq1zq46bB6DydGoorn3a0i8MJnBK4S7s2Fg7FQ0r8wcMQCJtA3eu/kArOBJPQFM1bn2dDR4c0cZiERM3e6MTjEk57riFYfnvM/35o9DweUXqdO8Ozt9oieHslfYqROeteoNEq9evZo0K/FutDO2EgtqnOsstop7DAbhXguXbbahKt25/Y5u3rihf378labTkqq1lsOg3A5nmQwne66j1bn8TGBwhw1d/eoJr9JTepmRLiSK/M4Sfka4QBzu2XBkRF4t0CB//gVCxdcR+MBH9I3q0lKX0BCEhFAt2M5iPFGn1RDZkF6+ONJiMdT9dz/Qb377gbY2O25lUP40Lk7EwrR4/e+NSEzl/DyoyaBhHR1LWqWi9vaa7v/iPQ3Oevr7X/6ml0eHWmu21G03CQnWaIAjB7M+AZe+oVcGpDhBU7Zt9NQBAqRYPnSl3jQ83g3lfxKwoCIs24ZZ5ruig5n65u4anh6QfCchuiW6pEpzGxJNSRxV6IYZPHSSsTSOxyMnf97c39XtO7e1tbXlNuQMNMCF9EtcAy/+0hheGIAYeB47C5DTmZa0f21L7777rr58+FT9wUxNZxtN1poFW+8OYquCSBTkDlkN6MiIKJObrnfV3UAoN4RZHn4KNCwYgvSiV6MCfxzMQvg2MHYgYcas1VKWPmalCcBxZjbDMMuaplClstKz9hHxQ1+Gg75q9ZJu3ritP/z+d7p988BJyGmq1wCzI+ECEIm1V30sdo/zb0VigOLBIYEgWggoEsLcZOJUQ+t7W/rV739r77aP/vxn9Xp9L69sk1uZ16zrjWUtnHrcSDZKIWS9SmBJUF5rz1AN0VbMzfOFt8wC3CAV/AdOQdCRzHvmxS93j2NxxoLUTJRvUuPg70yTkioqlk8WU0+PyMYzY3/q8Bc+G4y0qJb1zq0bOnjnundNjSkWNdooYcTNrbkI6nTNYyRyWK1SwAETcrtR0p0713T1H3v66sFjxyRC1lA9+hMQz4
Question 84+6NOTwWJJAGhDqNRoQvzyyYp6xmY9+GfwPs+j7VBO4M5YxH3YjgQ1FxNEI3S+y69idudv7Pm2gje12v7CBEhUvlKBVRxqODhTrTbXu/dv67/+83e6fftA9cQKwZ6FrSFUlVmTknt12fGNSMwHdBiKASLX6+zRG4gcIjnToKSta7v67R//4A2mP/7b39Q/PTUik2w5giZDsZ5naoYdZTHBQSa7NzJb4YcAqJMWhl7YFBsQJ0B7tqchWA1aAbg887tpOPN45m8AK0ul646xgCfmmlcBHEjJ5GEw2SIWXh53y1t3bqu7tu72gsQAnJrpC39eUhOkE4p8A+4hAJWc9RHem51Ga/Wyruyu6fadm3r6/LmGo57K1abYSZT977DqoUPGDQDCUlxgg/pGJ79Bid2j3IS0Qvgy+C/gR7NhU0wszIUHRY1aqCkjPYOTliaQ3BoZAB110/+YcrzG12niOQEKhGNsixwR3+/eu6X//K/f6f37173NmVk1Y0JkhfdYu58LTcaR587Ca+5K4fhGJM4Agfoul8uUmziXActFX7YPdvXbyh/UqFf1yUcf6fToiBg/AwfKYcQDFp6Z8TVAAwXQKFMXlBPki0jioLrLepKVjm8MslROEVH8bfqA8/wrvmPqjMumS0F1FsjsxS5949Zaj03QZUWj6UydjQ3dff897V47sGkctsiNTbSLuuBvGUhg9dqfkZ14MjQ6gL8sb5o6iXD+O7cP9Olnn+mLLx95bzdUkfCR9WrD9bEpoicL9TLrlggWjc9jtqq/AAjDmU9y72PSBSiClQMynpRG3Vw+R5ASopKwnqORFxQPqs1EoH5PBguRvJ/UeozyfKhWs6T37t/SH//4e929c1WtKrJRlMveHdA9+xR7p1JkETaCRLYKTuCb/fsWdiIDwn4Q6cKNTINEo2dE1I7JkFnR2v62Pvjdb13p3/70F/WOjo3EVfSTyawMxtNl+CwjZJrFdCOocLAOtqlnntzvp/GCWgLHAKepJ+f5txwyqEu+yEcUXn45Bs8qu0R9TYlTIQwjGgdyq0GFCcvf397S7bv31OmyV2s8zzprgjwplsn+7T9oFYONViNM7fB8gyHJWErav7qu/as7+urRA2txmOKTSV+l6tyxfKAMOnhT80T5g5XIPOibWgAgghqHYHYeciBwUN1YkYIeB0rHnVgTowYoMeWlAfFMQJcLQQoNiBWzZp0wvg2l+VAH17b16w/e0+1bV9Wogz9E1ROzGas9uEJdCPfknOAK3KKrlyEwbXkjJb4MHJkK8AzqZTjWwu6NYa+ztaE77913lz75xz91+PKV49HwLQAxRuOxZmxg04iM6i4PjQRL9mRqKhxWQMqOGR51BfIaH9FtWkUBMuW96dgMMjqa5oXbwLdpLhS6g1YkhAZYgtl05t3lARJStHXWKums19dgMjYVPrh5Q5s7O6o0cHynzBUCGBmBR6o4P1u9Uaiar1l1Uvh9QgPrSzlf32jqlx+8q4dfP9TjJ89Ua7S1sdl21NJR/8R5Kdh2AgHy7GwQo2AKOFe9zi6ewW6saqTUtDLACqQlyk5GKwgFMlomodXxZ2GO+e5VEArLKpBKXsy9ZTF1QsTY0wU+jHLZAmKfQgAAEZlJREFUwJGdtfCDGAzO1Ds5Vbst3b19Vb/69X3dvnV9KcTBjYGw5N+AWBqfQFyfM41Iz5AUz6tOnTv7HyMxX3uQjEgxP81burNSuV7WzsFVdTfWnX/3k39+rJfPnmowQT/IHsIl4Z9sJyBvOhiKcGBTb7BRbohWoWoD6KmODLsERC/5jA+IB/CTDYrXEsORFrkYwiJ7QaFQsiDjZGFcLZGoD72V7myhYf/UwufBjeu6efu2upvrKdCXir/rjw7F5EzND1QKvHGbDw6uWOWE3/KDh49VHtbUXd80UuDVFeYJ9O38QaUqGg0nGgwGXg3yJArIJT7WzU3pAF7XdLMnbpXRGIxKzfKRiGzGzRHe9iabeKNGOlAl2cp8Yv1vHcMXecZLeOaNVa9Otb+7o//4/a916+Y1bW+2AllZLdnsM01+3Bfy2K368LrGru5/JyTmc+r1BHFZwRUZL9ijrV5Tq7mpD37/Oy/Jf/3TWC9evIzZBiIDAMaSlKhjDBtpA0I0IKie2LTc4SqBwQHWaLTRJyF2mJUTIqOWsyCwooiJWPvDJWsRxXgiEnpvV9MSm8OhKUDnyz3M6SMtKhXtHRzo/Q9+pYPbt1Rt1TVBsIIlgnH7jj8GCDdRrJlWk4EiADMVubnR1G9+90tTtrPBQE+ePFO1XvUWtLh/jkaD2AfPO5DWTZ3ntciankbikpYFNTaeQogMyPxaUq8xl/My5kfRoOW7ILEQSIM7ZuWcjPBrQA+80Gw89JbAaFH6Z6eaTkfqtBt6/72b+s3/9Qv9+pfvqtVe6QhzVZ7SNMxs4uVwzcidW1w8fmckXlaVdIKMAKv/eBS7XTZrdbW3NnTv/fe9JHz5xRd6/uyJTk9PDUAnmkaChSFMhdn6ldYTKCJImWGdgZ/66kmQhTwLEh6AZVGFIYgBg+de/WI7XLQnJAPE92NoB56plccgM8LZ5taW7t17Vzffvat6t2kenr0kKjV2Iq0tqcaq3H/zjD7St2S8oU+AAGkhT9it9aZ+89tfOHXWn/70N714daj+AHaiaYVPSP5lb8ySzDERgW5czVDLVJibsapBtT1WF5oaQ5CFteAolgidxgfKz+DlgNByJdSdcxjbOXs/Q4D6Gk+GWkxHWt/o6hfv39d//edvdefObqyxdH06U1g6WfWS65hZx1SR25b7wAX3Xy9vfGckzvWYn5zE1geoiZxYhUbOZ6rNS1rf2dZvun/Q/sFVffTR3/XpJ5+aR5rMZ6pXqmbqrXqbzOyfDEI67AmXwbTXxQV4xyXAoOP2hY0OF0HAS5n6LilJKgg+C2tibRFOJVgDMWdTHkkBsZ036/i13rWTT9uh+MCypEYLLcGKZbm0bf/2TVoMctF+zo2asamjStpca+p3v/uVhcm///0f+ugf/9BsPhbZg9iUpVSqaTiYaDQaqVKur/bOuwgI2pOAYDbKLFc08iJswscjJpn9uHnBYUoLC+cIseMZm8KwuTj579Dnsz/LVJ1WU7PJRNgI9vav6/337+mDX9zT3t6GKby3QWb3UKxw2AnY/9rdz7KPARugWJKvbwfm90JiYBXqN5hzjCKkdSI6o77ahJsNy1tNHdy6qdZ6R9t7u/r044/15OHX6vcHalTZmyFSLYVgEO6cCI32YcgDkvrn8fA98osF428UgHfIPFySPqBwRuTEry/BYU85vAgWWownGk8njpmrsXq0u9rZvqI7d+7onVu3tHNwzTofrM9OZ4bwktBtWd7/5CQvKV65EEZXPDnrDss1BG+EH7dK6nQb+tUH73obheF4rAdffR37qDQqzhSJ1QvKWCGfXbliIdU8ty0NNIzWQok5hq49YUm0mtvpl0Ed764QP6YWvhxlr1ogoFc2VpIZDkULE6/T01fa39nSL395X/fv37ZL5cZGbDI/GY/ML8NC2FfJXnoXqGuGjduUB63QwNzQC8fvhcQsuQAd5TUrCoOA7hJp3YGisATz2EkJL6ztvT3n78Vk+/XBQz356qFOXx3p5PjYGgtYEDIMUaYlffNIwD4QlLYbPxMSc2Ftnz3OEPBYkmMo8oDYsQfAcSMhN62mrRhxRpOpkRhtCe6V16/f0O07d/Tu3fck4uaq5DJOy6wdymnd9/u5OxCAZCiBmoXFMPS3lVJF9cpCePzhktiql3X39jVNp/9L9eqf9NWXj83+2OdjhiNi7CsIcn3zl/gs9xhiwzurHmRKDETgbYFfIG2ynqa3PQVYJWkzGoXZzNbZ6Xio9U5Hm9sb2tnp6t27N/Uff/iVru5tpkkTK021gQAK4UETAeWFNw4KDOtoIZtK3LSEuEbq1NZVk7/RxdIcEvodfggnY6J0VRabblN5Adcc4YF52J32khR8plUmNH4606unL/Twyy/12aef6dmTJ46lsocVsam4alYjWybtdyOhAIlPNivBPg64+YHEqXLedX+ttUjSu51PwnxuPhtfhMVMlXpV1XpNzVZLOzs7un
Question 9f/vu69976am2v2oDRYTOHDMpl1yZlTX9aV4JcRIoPz4nXcZ4KmNxAHktUwGdT9gNzz/HhtzASK9KUaT6UPP/xKf/nrP/XgwddWAc7Y06LSVLVW12QCvPHVxnpI2bQU35VwxKLekB+YlEF0chvJWo+/sdWFFpADiV2O28L2vrG0IZCOhgP1eyf+5uDgqu7dvW3tw5WddW1tNj0G0ykrBOrENCaedRTmxoU114OVOkuH83WMeAJUfLK8uHDynZGYcjIAolExMnlF4LmpaWqzr91G3mPmzTUZjT2j+2d9PX3yWA//9aUefPWVjl68Mm8Fzxx0Jqif63PyvaQaqUVUNICnVOhYpkZMMvSL1XrdLA9849nZmd9DIwHPTuDr7du39c716xbiumtranXaaNdjRrqT/JeBG+ZqLj0O0eV4/m/8T/sDPnmkVgVchBuMRR7R/BarSX8oPXh0KHjkTz/9VIfHPe8uxOaPwJV931BjZmRmZcSEDuJRHjpwVGVohFjGMuEJCNKJudj0mwd2oo+h0mxOghcmFEaJqdV7G2td3bj1jt5//13deOeqdnfXlpMyaKzNOi7TvUlRHAkIS4gVYVmEw/KFbzl5O0h8oZLckItIfHGxq6XlhM/JzXtydKRnjx7ryaOv9fTxY716+tyORtPh2LwtCnD21EMpPllMNSC9LM5CDF9WUSWHe/w88PcgtQAIS/kgOftlrG2sOxnM9YMDsw5X9nZVbUZkhRWfkB+yW/LL+BZX/j/3r3DrrZ5muF0sFJRAQ9AfS18/OdI///mJPvzoH/r666eaTKaOgKjXm2ERTP7X3msaaylBB2Zf0PoEktI1b2Fsi2rq6gxjBfpfJIawRAJjdMBIEWtrTe3v7Yq0Zvv7u9rf39He3rbazVL4iNNoCG0iK0F+gu00s5Jn5MXOfY/rnxSJmdh2gMePAIseHlujiflkNkZ/+vVjnfV6Oj060ag/0JRteUdjW/1ATBzUA9iRUYdBgudDl8s570CF0PuC+KTM39jc0NWDA/3hj39Ut9NRE1MSCAul8nobAoz1tmlALsL3p0RidOPMMQSrF6/6+uzTz/334sULDUcTHR4eRYRzGetXGEIcdMDqx+rEnnDAPSUxDA1EIB1+L8BtNGTP7qlXsGa74T0zatWyvc0Oru06c9H2lU21WjgoBXTMR1vwAIljHYGq//8eiUOIyEtoyMhFhIAPw6VzPp0ZiaGeHiGo5hQ+TvY7HZ2R5nOkMSzB8alOT07UH/R1enamo6Mjn6MlYeeiJoAts4dyx3mEKbPd7ajRwBEbRG5pbX1dO9euBemBMkCZ8HOGF8T/Aaqefz8yJaYNb6LEJJuxIGgvu4rG46lOTk50dHSi3umZqfKgP1T/bKCTk1MdH5+o1zvTcDiym0C72Y0ggIJxyJTTJuNwaiIX8Pr6hvb39wW/u7u7JdITXL26q431FlFaXqAAHSx7VplZ52ueDyQGcPkY73NnyYJm+L6F4w9Kid+ExKAJDh7+Wfj3f0YolOcGAssfVjReIhkLr48Xmo+gFDPrR48PX+n0JLYNAFnR6WK+JriVpRe9b5UdPCnLnmesdWUtBoNAWMqFtPFj1mRqwvUlCOzXXnPfZXzP/96ExLQHwT7SyhKgha6WZAqxeINQw8FIg8FIp0enevnypV69PDQic29OLGCt5W5aZjAbQbb/MPoAL/T8bDa0ubnhnBjbV7bV7QRK5m5bXPRkCxCFliVkkhBHuR9vr47cW2k8vieYzn3+gyJxpih5+S3yxEZM+5xm0CQkAndAqpRCC+UJb7DlWCnxqca5HGwHFUXqhXp6UuCoAgtBSplUYxaPl4oYkgxj54q6swEARGdAl0h9DlSri9yf1Z23e5bh9o1SyTo0H4XgxgY1bj//0+dwgHKYf+FD5q3BMLdCSFM2+baZOOY1c5hg9iyewKb4G0CTtApcQ21NRzBWJFYkt9PtgFUxz03l3AnYro4/HBJ/Lz1xAVbf+RRtgoGBs72RKCCHMFEmK33AwtTDjuzUZBUQ/hVofcr48qX6I8URGcdBRmsq7DHGpAjXT4PXasmkUU6IztLoqqzCQ+dcYCmoMrXjO3f0LXwYbQy0QP+OugzEYdLHKh4eeagf0TWDrPYOBTxJQ0bSPn70h1NrTKbJJ4kuc5MVCao5Dy9FktosKkZvC4WMCfDhLf4DqQFjiQ13UuF5cctgy8d44e3+v9zHztTv7Zb9raXZ/xZFP5G/KMJTpAc2e6vLnDss1O+rwkJPBe9qaxwAN8yBYsm5MPIekzHoDJhHJpT0qI7y+xQKAmAx9HkewFVtnHmwCscfckDO13zhykoTfDbYSxqWK6ibMynBEtBGFh/3L8HFNymHfiLDFlqfOpZBCPJ6IQJAfi2ML47mwLBVIqQ/axrSx3aGStspuOIo3/9nwKW5caE3b+2yNJlMFiBPntHFkvNyUbxXPH8dk36RauXri+wE35sSFOBK+e47xDOfp0ozTHgdBDYSFxtUOM9lMBj5u1y2v8+DXfgmBm51Y/ldal/ux+v6vfryBzqzYYSG81f0VyvZBB/NTI2lCXTgG51ID5jYfjW95E4F8tLPbNDJR74K3zUbnBNaUgDkO69aF64zwBI4gnNPF2/x8NOzE0WYF8+L8L/Q4eW4XLh/7jKVdfFdrpfVLE/Ofbm6yGV823urL37YMyauESYQMPeNiJglIuWbxZYU259nYGKjVljOh/FxOMFHAdkIskLmc4UVa/nJzn8yJDa4GIvLgP4t4CiC8VtevZTSf9s3PM9EJB//nW9+nHfoPZS3MBnfVPFFYPk6LYH5O+4xDoV3vcrl2MjC46QrSl/yQeGjc+e58B/++JMisWFXhEGhv5fdzvc4Bj9cgGXhW06ZHBkBz52nZxdeP3eZv8s3L86z3I78/Mc8Lif9BaRbtiFkWId5Le+lSUm7c98ijwRvBI3NgljxGxA7axdgGJx/4twLXPhJkgyp4ceHzk+GxN+AxSU3iuBYDt4l712kIvmVIvIu7+WT1xzzIF98XETk1+HPxW/e9rVhcLEhVFIAVLR/kSOgUhMijVhw0hc+8MeXMQsXemm/hzQJqOQccDPy5uPb7vmby/tJkTgDNY/LUjzINwpt/wYSX3znAswLn/r0G99ffOHC9euQ+cJr/4dcngdGzqtnVtktxAeC7Yuhm4FodlFN+J/nQAjKSatRnBnLXmYpGR08Ah66u2LduaT8QfFZvvf2jz8qEtPFjGsXj2/q2qUIeBFebyrgez67WNXF6+9Z/Pf7vACcmHgr1C0WnGlt9mooPstK44xyWSN57h0uTIEzqcm6+Z8eGqUZphhm5KVM0Te6cekN4PjvUi4oADP+4vHSgl9zszBul77x77bl0o9fczOX+W11v+bzt3b7svpz26KSjIoB47i3osEXkRgUvKxMq8OKlAa74E+Pr5fC8XuZnS8t8eebP0PgR4ZAXht+5Gp/ru5nCLw9CPyMxG8Plj+X9BNB4Gck/okA/3O1bw8CPyPx24PlzyX9RBD4GYl/IsD/XO3bg8D/B01y5dlO9XiAAAAAAElFTkSuQmCC />
1. antibonding
Question 10What is the correct order of carbon-carbon bond lengths in ethane, ethylene and acetylene?
1.ethane < ethylene < acetylene
2.ethane < acetylene < ethylene
3.ethylene < ethane < acetylene
4.ethylene < acetylene < ethane
5.acetylene < ethane < ethylene
6.acetylene < ethylene < ethane