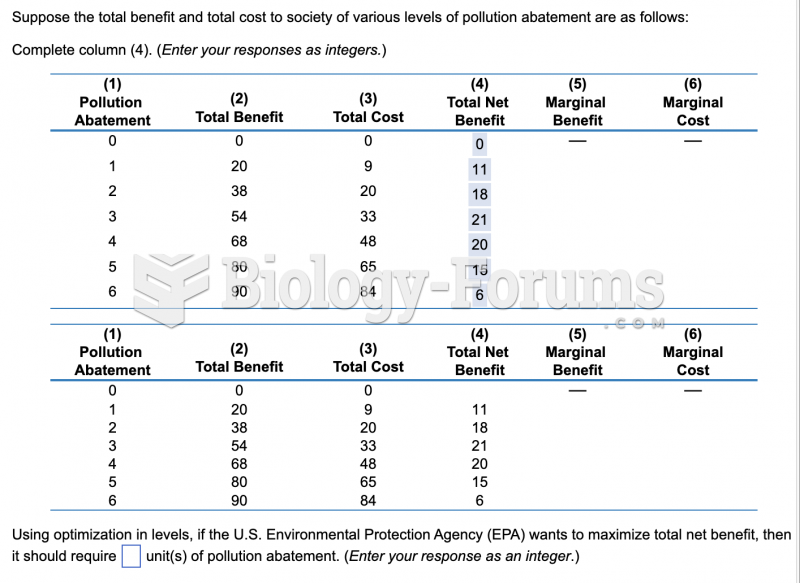
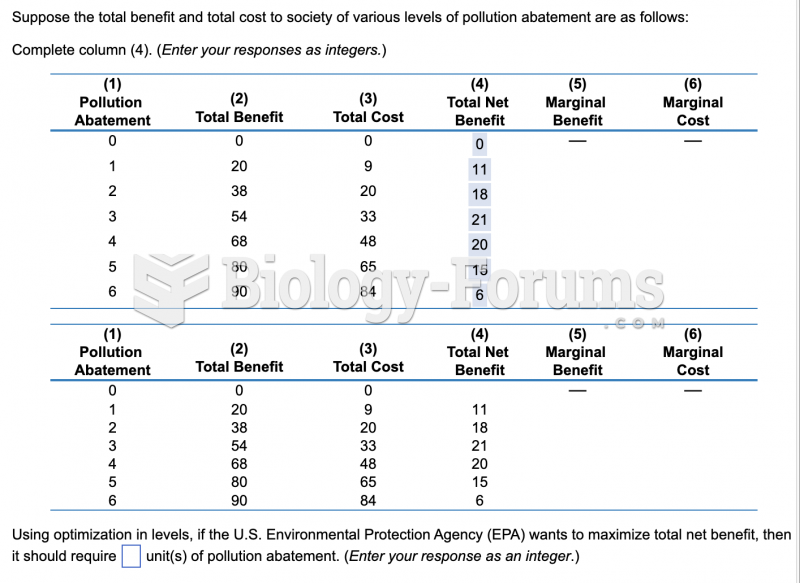
|
|
|
The top 10 most important tips that will help you grow old gracefully include (1) quit smoking, (2) keep your weight down, (3) take supplements, (4) skip a meal each day or fast 1 day per week, (5) get a pet, (6) get medical help for chronic pain, (7) walk regularly, (8) reduce arguments, (9) put live plants in your living space, and (10) do some weight training.
In the ancient and medieval periods, dysentery killed about ? of all babies before they reach 12 months of age. The disease was transferred through contaminated drinking water, because there was no way to adequately dispose of sewage, which contaminated the water.
Blastomycosis is often misdiagnosed, resulting in tragic outcomes. It is caused by a fungus living in moist soil, in wooded areas of the United States and Canada. If inhaled, the fungus can cause mild breathing problems that may worsen and cause serious illness and even death.
The calories found in one piece of cherry cheesecake could light a 60-watt light bulb for 1.5 hours.
For about 100 years, scientists thought that peptic ulcers were caused by stress, spicy food, and alcohol. Later, researchers added stomach acid to the list of causes and began treating ulcers with antacids. Now it is known that peptic ulcers are predominantly caused by Helicobacter pylori, a spiral-shaped bacterium that normally exist in the stomach.