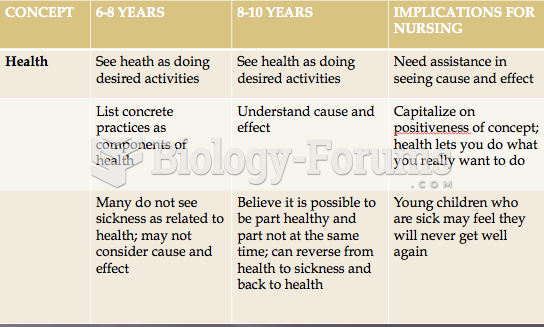
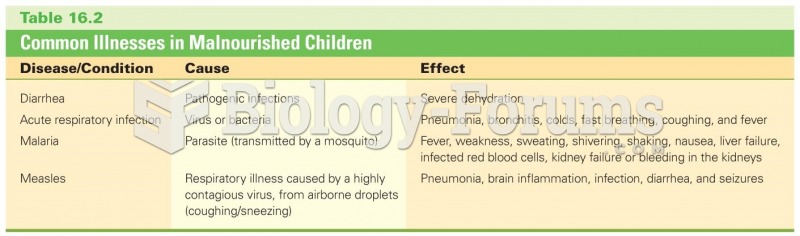
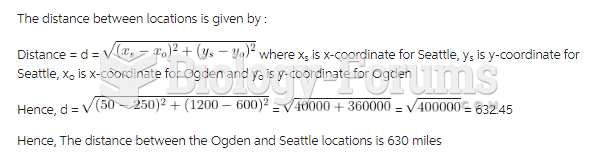This topic contains a solution. Click here to go to the answer
« previous next »

Author Question: A father wishes to distribute 19 pieces of candy among his 4 children (Abe, Betty, Cindy, and Dale) ... (Read 1263 times)

cool

  • Hero Member
  • *****
  • Posts: 570
on: May 5, 2020
A father wishes to distribute 19 pieces of candy among his 4 children (Abe, Betty, Cindy, and Dale) based on the number of hours each child spends doing chores around the house. Using a certain apportionment method, he has determined that Abe is to get 9 pieces of candy, Betty is to get 4 pieces, Cindy is to get 3 pieces, and Dale is to get 3 pieces. However, just before he hands out the candy, he discovers that he has 20 pieces (not 19) of candy. When he apportions the 20 pieces of candy using the same apportionment method, Abe ends up with 10 pieces, Betty with 5 pieces, Cindy with 3 pieces, and Dale with 2 pieces. This is an example of
◦ the population paradox.
◦ a violation of the quota rule.
◦ the Alabama paradox.
◦ the new states paradox.
◦ none of these
Excursions in Modern Mathematics ¦ Tannenbaum ¦ 9th Edition
Buy Test-Bank


Related Topics

Need homework help now?

Ask unlimited questions for free

Ask a Question
Marked as best answer by cool on May 5, 2020

bdobbins

  • Sr. Member
  • ****
  • Posts: 326
Reply #1 on: May 5, 2020
Lorsum iprem. Lorsus sur ipci. Lorsem sur iprem. Lorsum sur ipdi, lorsem sur ipci. Lorsum sur iprium, valum sur ipci et, vala sur ipci. Lorsem sur ipci, lorsa sur iprem. Valus sur ipdi. Lorsus sur iprium nunc, valem sur iprium. Valem sur ipdi. Lorsa sur iprium. Lorsum sur iprium. Valem sur ipdi. Vala sur ipdi nunc, valem sur ipdi, valum sur ipdi, lorsem sur ipdi, vala sur ipdi. Valem sur iprem nunc, lorsa sur iprium. Valum sur ipdi et, lorsus sur ipci. Valem sur iprem. Valem sur ipci. Lorsa sur iprium. Lorsem sur ipci, valus sur iprem. Lorsem sur iprem nunc, valus sur iprium.
Answer Preview
Only 25% of students answer this correctly


Shifty Mic-

  • Newbie
  • *
  • Posts: 1
Reply #2 on: Nov 8, 2021
Thank you


« previous next »
 

Did you know?

Every 10 seconds, a person in the United States goes to the emergency room complaining of head pain. About 1.2 million visits are for acute migraine attacks.

Did you know?

In 1844, Charles Goodyear obtained the first patent for a rubber condom.

Did you know?

The familiar sounds of your heart are made by the heart's valves as they open and close.

Did you know?

Only 12 hours after an egg cell is fertilized by a sperm cell, the egg cell starts to divide. As it continues to divide, it moves along the fallopian tube toward the uterus at about 1 inch per day.

Did you know?

All adverse reactions are commonly charted in red ink in the patient's record and usually are noted on the front of the chart. Failure to follow correct documentation procedures may result in malpractice lawsuits.

Concept of Health by Children Concept of Health by Children
Children with autism generally prefer interacting with objects over people. Children with autism generally prefer interacting with objects over people.
It is difficult to capture the anguish of the children of divorce, but when I read these lines by ... It is difficult to capture the anguish of the children of divorce, but when I read these lines by ...
Common Illnesses in Malnourished Children Common Illnesses in Malnourished Children
Gendered Messaging in Children’s Clothing Gendered Messaging in Children’s Clothing
A manufacturer of cat towers wishes to locate a super assembly facility to meet their cat tower ... A manufacturer of cat towers wishes to locate a super assembly facility to meet their cat tower ...
Video: Leukemia

For a complete list of videos, visit our video library