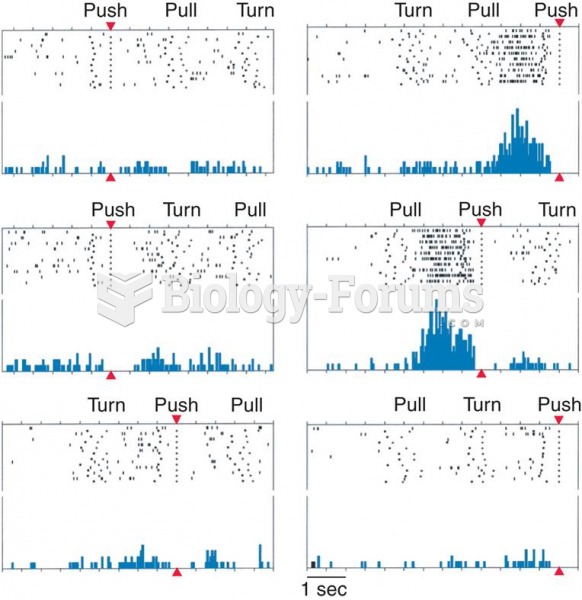
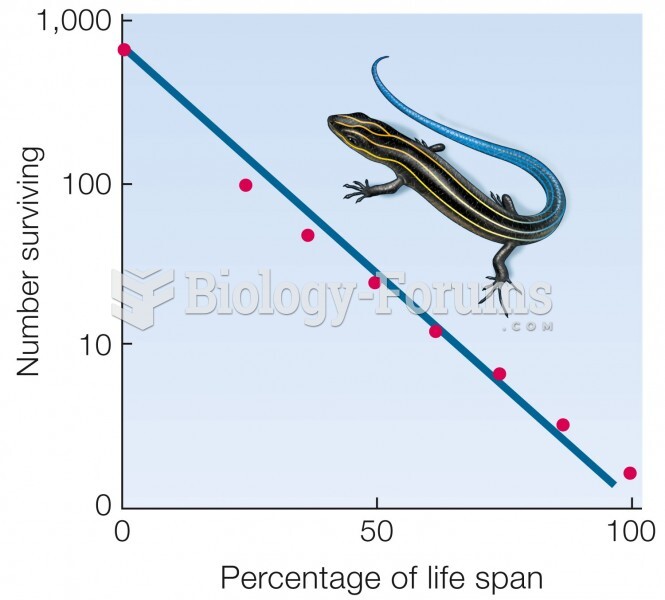
|
|
|
Did you know?
Cocaine was isolated in 1860 and first used as a local anesthetic in 1884. Its first clinical use was by Sigmund Freud to wean a patient from morphine addiction. The fictional character Sherlock Holmes was supposed to be addicted to cocaine by injection.
Did you know?
Every 10 seconds, a person in the United States goes to the emergency room complaining of head pain. About 1.2 million visits are for acute migraine attacks.
Did you know?
The human body produces and destroys 15 million blood cells every second.
Did you know?
People about to have surgery must tell their health care providers about all supplements they take.
Did you know?
There are 20 feet of blood vessels in each square inch of human skin.