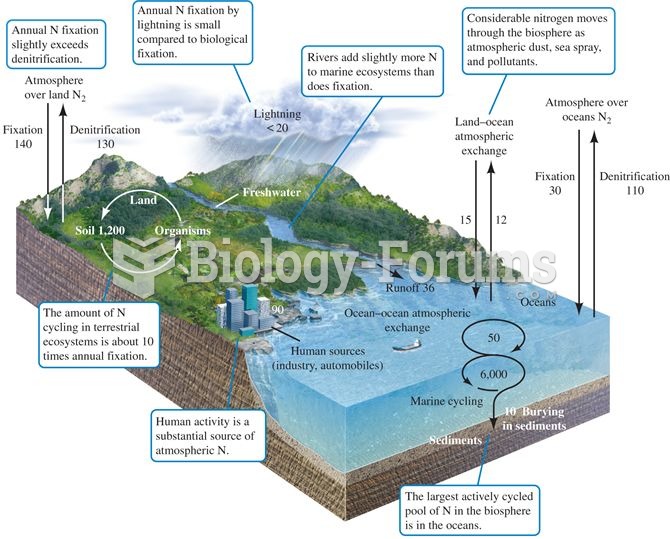
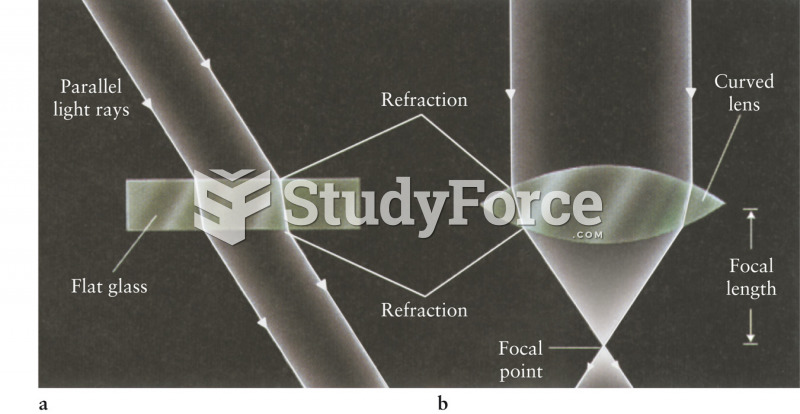
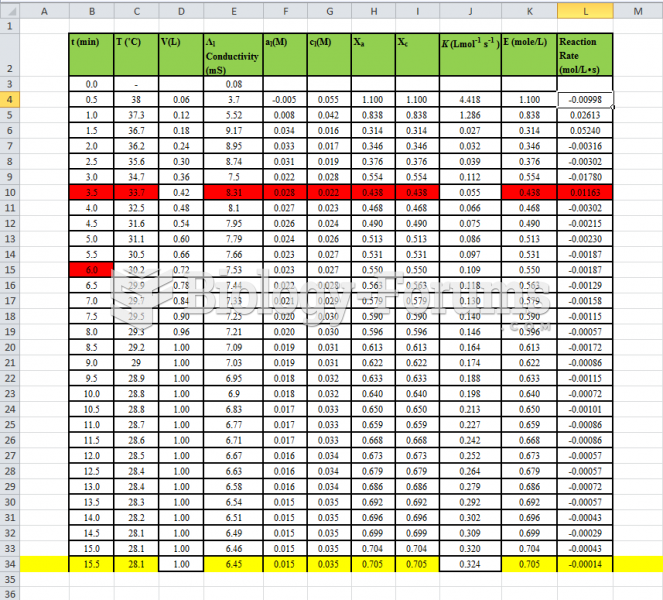
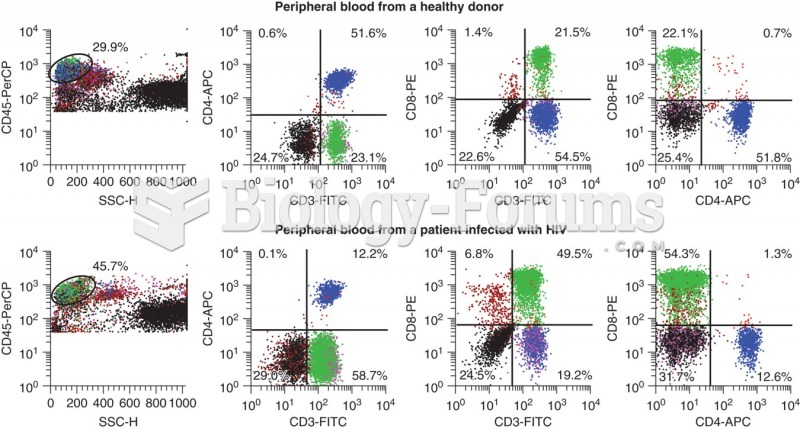
|
|
|
Asthma cases in Americans are about 75% higher today than they were in 1980.
Once thought to have neurofibromatosis, Joseph Merrick (also known as "the elephant man") is now, in retrospect, thought by clinical experts to have had Proteus syndrome. This endocrine disease causes continued and abnormal growth of the bones, muscles, skin, and so on and can become completely debilitating with severe deformities occurring anywhere on the body.
A serious new warning has been established for pregnant women against taking ACE inhibitors during pregnancy. In the study, the risk of major birth defects in children whose mothers took ACE inhibitors during the first trimester was nearly three times higher than in children whose mothers didn't take ACE inhibitors. Physicians can prescribe alternative medications for pregnant women who have symptoms of high blood pressure.
If you use artificial sweeteners, such as cyclamates, your eyes may be more sensitive to light. Other factors that will make your eyes more sensitive to light include use of antibiotics, oral contraceptives, hypertension medications, diuretics, and antidiabetic medications.
When Gabriel Fahrenheit invented the first mercury thermometer, he called "zero degrees" the lowest temperature he was able to attain with a mixture of ice and salt. For the upper point of his scale, he used 96°, which he measured as normal human body temperature (we know it to be 98.6° today because of more accurate thermometers).