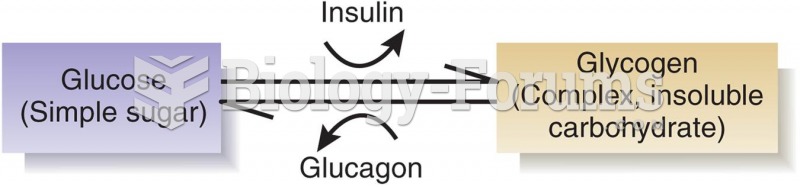
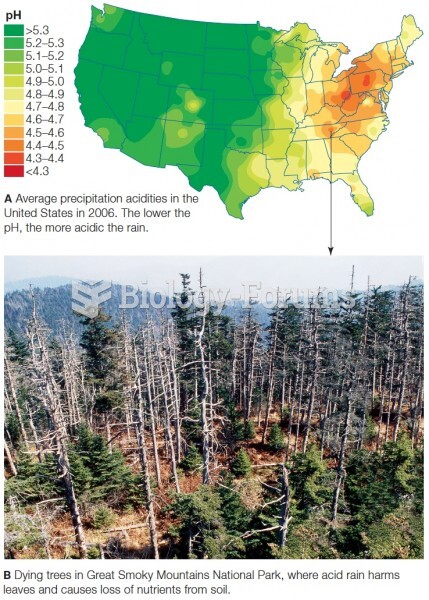
|
|
|
To maintain good kidney function, you should drink at least 3 quarts of water daily. Water dilutes urine and helps prevent concentrations of salts and minerals that can lead to kidney stone formation. Chronic dehydration is a major contributor to the development of kidney stones.
The first monoclonal antibodies were made exclusively from mouse cells. Some are now fully human, which means they are likely to be safer and may be more effective than older monoclonal antibodies.
It is widely believed that giving a daily oral dose of aspirin to heart attack patients improves their chances of survival because the aspirin blocks the formation of new blood clots.
Liver spots have nothing whatsoever to do with the liver. They are a type of freckles commonly seen in older adults who have been out in the sun without sufficient sunscreen.
Pregnant women usually experience a heightened sense of smell beginning late in the first trimester. Some experts call this the body's way of protecting a pregnant woman from foods that are unsafe for the fetus.