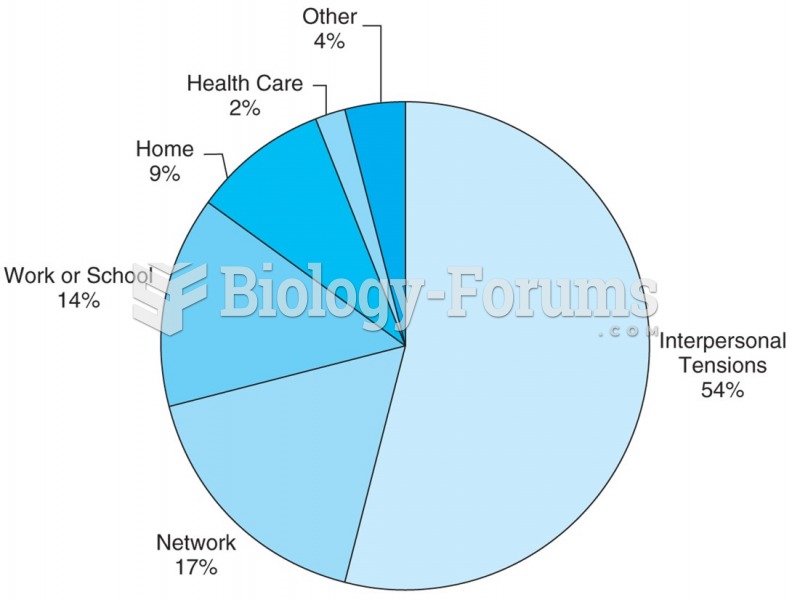
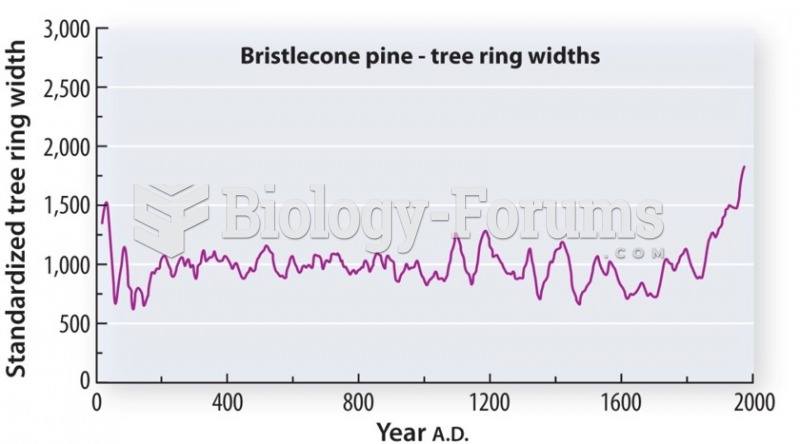
|
|
|
Today, nearly 8 out of 10 pregnant women living with HIV (about 1.1 million), receive antiretrovirals.
More than one-third of adult Americans are obese. Diseases that kill the largest number of people annually, such as heart disease, cancer, diabetes, stroke, and hypertension, can be attributed to diet.
The most dangerous mercury compound, dimethyl mercury, is so toxic that even a few microliters spilled on the skin can cause death. Mercury has been shown to accumulate in higher amounts in the following types of fish than other types: swordfish, shark, mackerel, tilefish, crab, and tuna.
Illness; diuretics; laxative abuse; hot weather; exercise; sweating; caffeine; alcoholic beverages; starvation diets; inadequate carbohydrate consumption; and diets high in protein, salt, or fiber can cause people to become dehydrated.
Fungal nail infections account for up to 30% of all skin infections. They affect 5% of the general population—mostly people over the age of 70.
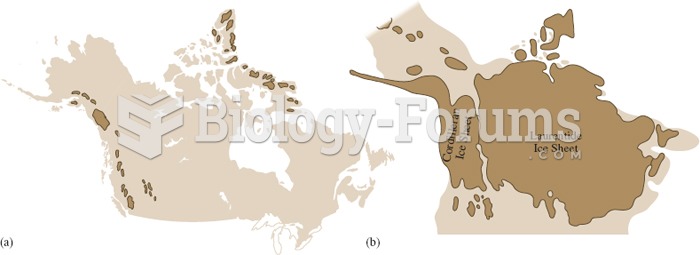 Distribution of glaciers in North America (a) in the late twentieth century, and (b) 18,000 years ag
Distribution of glaciers in North America (a) in the late twentieth century, and (b) 18,000 years ag
 In 2008, the U.S. economy suffered a gaping wound as several trillion dollars were ripped out of it.
In 2008, the U.S. economy suffered a gaping wound as several trillion dollars were ripped out of it.
 The age-related increase in spirituality is different for two cohorts born seven years apart. The ...
The age-related increase in spirituality is different for two cohorts born seven years apart. The ...