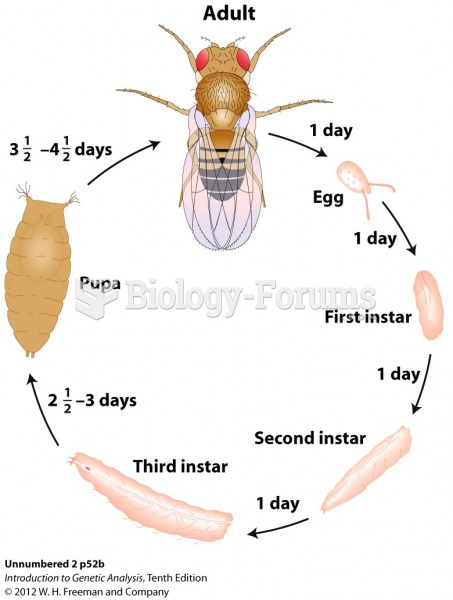
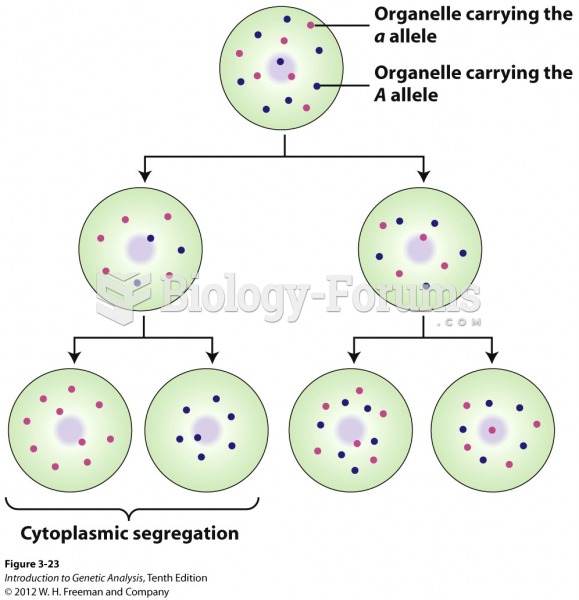
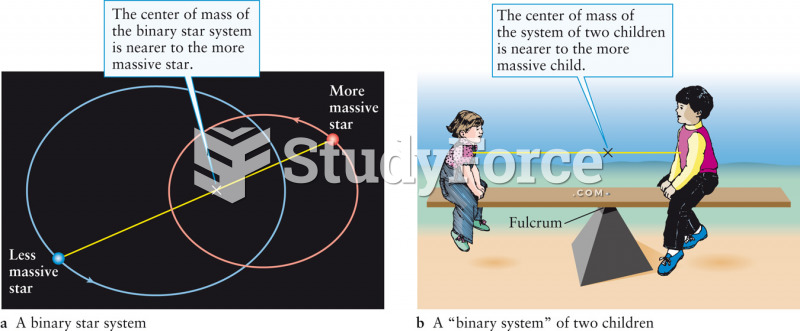
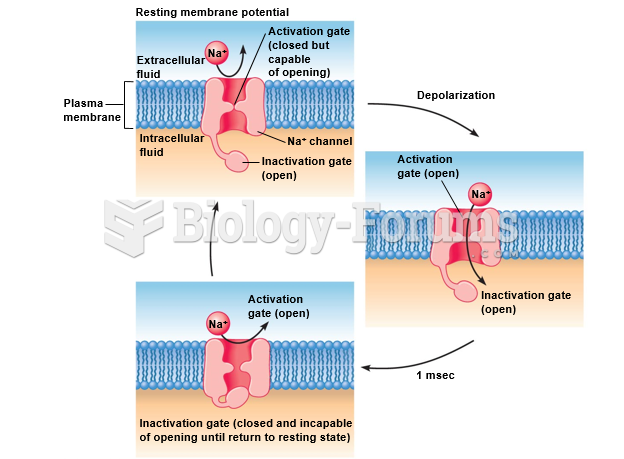
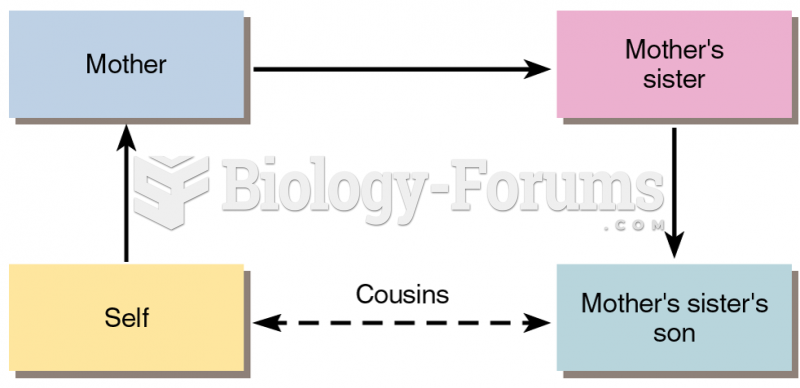
|
|
|
Studies show that systolic blood pressure can be significantly lowered by taking statins. In fact, the higher the patient's baseline blood pressure, the greater the effect of statins on his or her blood pressure.
Glaucoma is a leading cause of blindness. As of yet, there is no cure. Everyone is at risk, and there may be no warning signs. It is six to eight times more common in African Americans than in whites. The best and most effective way to detect glaucoma is to receive a dilated eye examination.
GI conditions that will keep you out of the U.S. armed services include ulcers, varices, fistulas, esophagitis, gastritis, congenital abnormalities, inflammatory bowel disease, enteritis, colitis, proctitis, duodenal diverticula, malabsorption syndromes, hepatitis, cirrhosis, cysts, abscesses, pancreatitis, polyps, certain hemorrhoids, splenomegaly, hernias, recent abdominal surgery, GI bypass or stomach stapling, and artificial GI openings.
According to the CDC, approximately 31.7% of the U.S. population has high low-density lipoprotein (LDL) or "bad cholesterol" levels.
The average office desk has 400 times more bacteria on it than a toilet.