This topic contains a solution. Click here to go to the answer
« previous next »

Author Question: The total area under the curve of any continuous distribution is 1.0 as long as the distribution is ... (Read 91 times)

Alygatorr01285

  • Hero Member
  • *****
  • Posts: 564
on: Jul 24, 2018
The total area under the curve of any continuous distribution is 1.0 as long as the distribution is symmetric around the mean value.
  Indicate whether the statement is true or false

Question 2

If P(A) = 0.3, P(B) = 0.6, and P(A and B) = 0.18, then A and B are independent events.
  Indicate whether the statement is true or false


Related Topics

Need homework help now?

Ask unlimited questions for free

Ask a Question
Marked as best answer by a Subject Expert

lcapri7

  • Sr. Member
  • ****
  • Posts: 350
Reply #1 on: Jul 24, 2018
Answer to Question 1

F

Answer to Question 2

T


Alygatorr01285

  • Hero Member
  • *****
  • Posts: 564
Reply #2 on: Jul 24, 2018
TY


lcapri7

  • Sr. Member
  • ****
  • Posts: 350
Reply #3 on: Jul 24, 2018
You're welcome


« previous next »
 

Did you know?

The heart is located in the center of the chest, with part of it tipped slightly so that it taps against the left side of the chest.

Did you know?

Parkinson's disease is both chronic and progressive. This means that it persists over a long period of time and that its symptoms grow worse over time.

Did you know?

The top five reasons that children stay home from school are as follows: colds, stomach flu (gastroenteritis), ear infection (otitis media), pink eye (conjunctivitis), and sore throat.

Did you know?

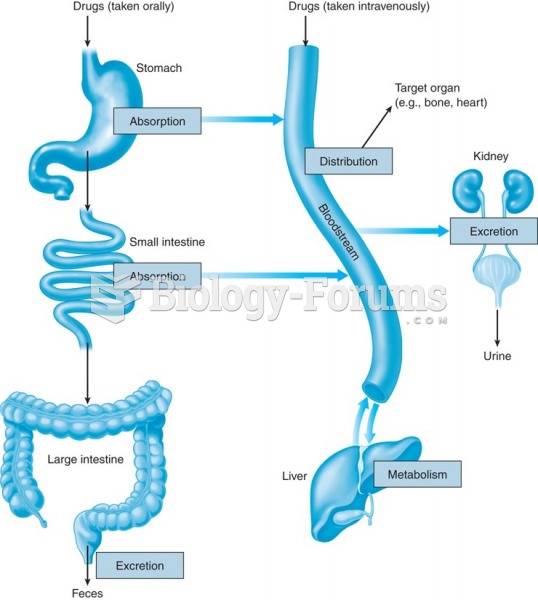
Disorders that may affect pharmacodynamics include genetic mutations, malnutrition, thyrotoxicosis, myasthenia gravis, Parkinson's disease, and certain forms of insulin-resistant diabetes mellitus.

Did you know?

Coca-Cola originally used coca leaves and caffeine from the African kola nut. It was advertised as a therapeutic agent and "pickerupper." Eventually, its formulation was changed, and the coca leaves were removed because of the effects of regulation on cocaine-related products.

Beaker with ibex, dogs, and long-necked birds, from southwest Iran. Beaker with ibex, dogs, and long-necked birds, from southwest Iran.
Movement of a drug through the body (pharmacokinetics): absorption, distribution, metabolism, and ... Movement of a drug through the body (pharmacokinetics): absorption, distribution, metabolism, and ...
Basic massage practice office area. Basic massage practice office area.
How to find the area of composite figures (Part 1) How to find the area of composite figures (Part 1)
Piecewise Derivative Example (Continuous or not) Piecewise Derivative Example (Continuous or not)
A pipe that is 0.46 m long and open at both ends vibrates in the second overtone with a ... A pipe that is 0.46 m long and open at both ends vibrates in the second overtone with a ...
Video: Mendel's Principles of Inheritance (Father of Genetics)

For a complete list of videos, visit our video library