This topic contains a solution. Click here to go to the answer
« previous next »

Author Question: The figure below is a graph of an electric potential as a function of position. If a positively ... (Read 79 times)

imowrer

  • Hero Member
  • *****
  • Posts: 514
on: Jul 28, 2018
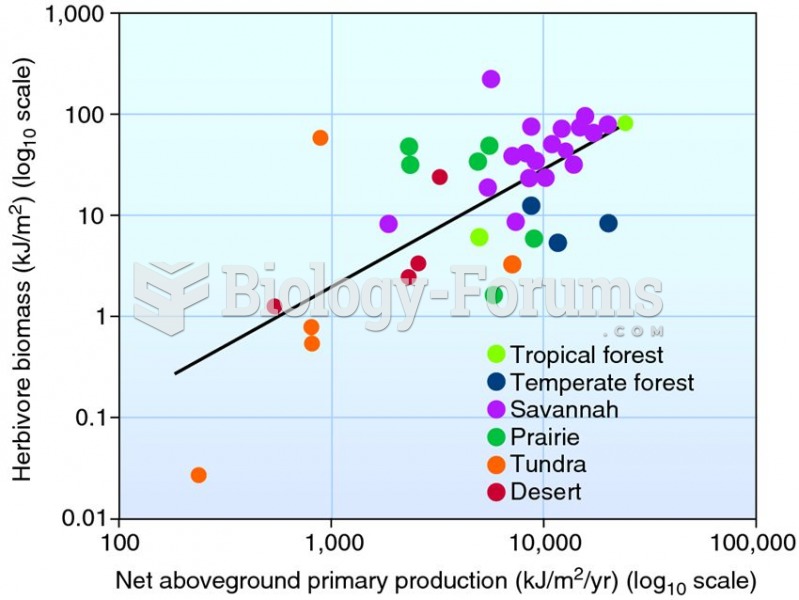
The figure below is a graph of an electric potential as a function of position. If a positively charged particle is placed at point A, what will its subsequent motion be? It will
 
Question 2

jPcdzMx/DsCJbKhs+U6tt9sWaGAfRlXsnHtmzi9XtYfuf11L3/V4ycfKU4L9PvnmXiN9QR7VnKsJseorA8vVX2tQHc90LN5N/UA5wM8CMPcek43mAqKJhbP/jjC0a5d6wHvwH9iXYk0JYjUbd2MQsnT8BMxEllhbGCQBlOQw39z/8x5d+9Ds/zVfPrdtx92mwqI+YA5SspmUvNVR+y6NaLaHz3FaycbhgqFdvHt+LQsIfogOFU3P5bCsqPC5520uY06AM5mgnsDb2neVhQjvPQIyV7Z0GP5lOdNmNvO4/5Q8Yw5PuTSKSks4r2AipYAAAQKElEQVSEOoNzbMWibP3dHPa8My9jjZ+MNSMMoNQcNW9bz5JbLiK+5F28whi+CCaLFqXl4dQ3ERpxKmNvfYxon8FKEk09bafN5agPRBPQBDSBzicgQYeSL51Pyef+h1RjY+s0kijVhwk5Hqse+jHxyrbGzEEMoPOPsuP22GUNoKRhJ13JjoPa9cv51/QfEt+wGCOvG2HXVsohDg6pujqKxn6ecbc8SqRHX7V+WDQl0/xpu+NOud6yJqAJaAIBAcnylKXsosnkDxhNItGIZYh4GnjRAuI7NrDq/ltIeUmVR+GJJnIGLV3WAIqFC1thqlf9i8XTfoCzbTnkiufnE7eCOUHqquh96lcZffODhAuL1GnTgZgMunr1UDQBTeCwCIikofTcDBf0YfDVt2DZUZXE5JqmupfaOQXs+eff+fC39ynvUFqjZdLSZQ2gYRlULnyNZTMugqrt2LECDN/Glg7vXgK/vpFen7uAYZNnQ04eviOFu5nnwmfSxajHogloAp1LQBW6G4ZSvioaNZ5+370aJ5FSOqFKDcswsbOjbPjtA1S+/zqhDIucdSkDKPVUbqsN27ngRRbefgV+XR1uLLq3xs/zU7hNTfT98g8ov/4urHBMFRCb0gYiw55eOverovemCWgCGUdADJoUybe6B0PO+SHdTzkLr75WastUEbxtR0mSYtUDN9O0a5tCIJq2kh3a1V2KLmUApRO7ZcC2V//IBz+5jqx4CjMSUcW5ngVm0iHZ3MKA70yk/MqZhKXgVgnzivp+ZrnuGfdF1APSBDSBTicgd0VlBMQLVPdKi2GXziQ0YDCmiNZLIqGfIhTJI7V1FWsemknKd3BMS3mJwac6/bDbbYddygDKxOzWF3/N6jkTMd0kfraBY0rLnDAk45BwGHDhjZR9fzKeb+BJrzm9aAKagCagCXwiAdPzkCL5SPdSyq+4E9cuwHTiOLan2pKJcP3ut55j0zP3IUJ4bgb4FGlvAFVfuFZHe/MfHmHl/TdimyG8rCw8kT3zbUi04LoGA66+kbJzrwyeZETU2sxM9YJPvJL1CpqAJqAJHCwB6R9oik/n03PMaRzznWvxmuuUTigiNmJmqfnAbU/fw85331SavpKNr/qCSj1FF1zS3gCK+JLM3a371SzWPDoVKysbN5yFadh4pkUqVYlneAy/dhYDvniJmuVTbr0hpQ5d8IzoQ9YENAFN4EgQMKQ8vu0P9P3mD+h1yjkY9Q24Ulfte1hWRM39rXrwelp2bAIRtVdNq7tmkmEXMIA+qx+Zxvpf3Y0dy1OKL7600PENwo1NOKFiym+4nz5nnovjua3Znkfi6tH71AQ0AU0gMwioDiZGiCFX3U5W/zK85ibliEiZmZGdg7d9PUsfnIKXigfF88oB7HpeYFoaQBGolsXzUiz/+Y1seuYxzNwCpU7gmD7SZsxp3o2fW8TYHz9I6alflMbuwYkQMTu9aAKagCagCRwyAVPCZz5ECrsz4qqZasrJdFIqM1RUtIycHtS88zJrfnWvirp5qn9gWpqTAzJIyyO2VMuiZpb/ZCI7/vIE4bwYId9Cehpn+UnMxmoi+ccweuqD9Bh3Gq4YP0mGUWHPzOvwdMAzqN/UBDQBTaADCEiXHFm6VZzGMd+7hkSiAdND/RXrmBXNZ+uf5rJz3nPq3tsVXY+0NIDJxhqW3Hkp2177HSHx/AwxfmLjPNyGBtySoYyaPpfCEZ/CyYBalA64dvUmNQFNQBNoNwIDvn4Zvc44h5amBvxWw2iYNraZYuVDU2nYsq5LVlkfUQOolAZUAaYfZBoBzdU7WDLzMmr/+Q8iOUVqklWeNlwT3IZ6QgPHcPy0h8kvH6XUC0zDQ/t87Xad6w1pApqAJrAPAd8XATSLssunkzuwDCfeiC91gNJXMFKIW72HFffegBOvCz7XhTJCj6gBFFrKCIr4uAkNOz9k4YxLqF70OlZenvL5DN/Ft5Kk6muIDR3HsdMfJr//MNRJMQxMmRA84qPY53rRv2gCmoAmkDEEfMPCcyGcV8yoK2dhxvLxEnW4lo/hOdjRQuqXLGDVo3eoSJ3MSHUVG5gWpkNUWpo2r2HZtO/SsupdsmPdVC2KUHQMSNQ30H3Upxl168PEeg0iIZOwbX54xlxmeiCagCagCaQfAVVWhqvKIHJHnsCgH0wmmXIxjBS+7yGCaaGcfHb+5VdseuFxJIHGaO0ykX6j2feIOtUAyjyeejLwXaS3hpo0NQxq1y7i/WnnEd+0DiO3CMn0tP2Q6unn1tfQ88QvMGr6/cQKStTnw563Nw6973D0b5qAJqAJaALtSUDJnUm0TZk1n/5nT2DAF87Dq61H5CmRzHzDwsiOsu6JO6lc9nbQi9X1UO2T0jg7plMNoALpOyjtABW+NKhaNJ/3p19Ey67tmFLn5/mY4vmZLaSa6ig+86tU3HQ/dm539bQh2bmGZSFNcPWiCWgCmoAm0NEEDAwxdHLPlukq6R948Y3EKk6DhhoVjTMMiZHaWPEUK+6dQlPVDjxLdERdpdXc0Ud4qNvvfCti+LiGjW3Azrf+H8tuuxSzejfhaEylw4jqi+t7JBsa6X32eYyZ9HOsSC6GKy53ZjVjPNSTpj+nCWgCmsCRICAzT64kv0TzGXHNnVjd++EnkkqTWZRizOwo7sZlrLx/CoaTwDJDR+Iw/+N9doIBlAhx0HdY1AUgRBiDD1/5HUt/ejVushGiURXaNH0Lz2vBb2xi4DlXMuKqu8DKUgbRlwaNShbtPx6bXlET0AQ0AU2gHQnI7J5kLJou5PUrY+iVt5IyPBwniYmNa3o4Bfk0zHuB9b++R01z+b75kayY9IqHdoIBBCVo7fqoKLIBm557nJVzJhNyHKyQ9PKzlHvtuY24LQ4Dv38dQy65GTF6yuwZ0gYp0Khrx3OpN6UJaAKagCZwkASUOrP840Ovkz7PwG9dBU2N0h8CwzcJmSGsWB6bfz+XD9/4X9WG1ZHVRaoyvexfxxcQiNmzxHOzpCefx5qn57DugVtQnnFYmmrIGgZeMonj+pT/cAaDJ0wKQLkyW6gVrQ/y+tSrawKagCbQ8QQMH8f3Gfyda+gx/mukGsUIgu+6OLZFyPBYe/8MatcuVpmhYgn9NOtQ0EEeYGDmVT0IXmv2kMOquVPZ+NRs7EgM7DCG7+OZBk6yQU2yjrzmbvp/9QLU04I8XqgmjWn2yNDxl5XegyagCWgCaU9AxfR8V9ViD7vyNmIDh+I31eNJ3aCodkXDpBqqWf/Tm0nV7QoSaXCDsGjgQB7xMXaQAVRK1qrUQYKYbkucD+7+EVv+MJesaBTPDmH4Nr4EkluqMbIKGT3xbnqcda7y/ASfLRlH0gFee4BH/CLRB6AJaAKawP8loOoDzUCHK6uwmOHXzcKMFmC2NKHu3K5FKBqjduNCVtw3HcdzVDxQagel4UFrIdz/3Wyn/t4xBtA3cMXVNQ2S9btYdOdl7Pnbr7HyivGtkDjCKi7sNjUTzivh2JsepPjTX8IVuQGp8ev4yGynQtY70wQ0AU0gkwlInK6w/DgGX3ErnpNAdY4I7vRKz7n6jefY8PR9yp0Rp0gMTzpMbrWvAVTRysCyixpAfNcWFk6/mMoFL2HnFWOKlLiouEi3h8Y6zJKBjJz2BN2OO0U1WQz7Jp4p5k+HPTP5y6LHpgloAplFQIyZ6/n0+8zX6H3ulSSaW5Ni5HXTxYzmsvl397DtjeeV5VNOUBogaD8D6Ht4nofjydSdQf26ZSyccj61y98JRK3FrPmG6t7uNNSQM2g0J8z4BYXlY5QeqKprtwws0fZMi2eDNDg7+hA0AU1AE+gyBAKzVv796yk6+WySTXswDR9bVL+kHNBtYeUj02nes1vld6TDsNrPAOLhiAEzDSqX/JMl0y+kZevyQNez1aEzfHDqa8irOIljZz5OTt+hSmRV+vylgzucDidEH4MmoAloAl2RgOpF7vkYdoiRV99B9oAKkvEG4raF1dCImVfKiPOvJ1RQqHq7qjqKIzzQwzSArdOYPniGrQrct735LEtnnE+yZidmtBhHdVA0EBGXZH0tPcZ/hdHTniC7uETVhWCmWuf8tAk8wteC3r0moAloAodEQHwcx/DUfd6TTvJFPRk1cTZGtABjdzXGoBGMvfVRSj/3bYyQvbcL0CHtrB0/dFit9ETZxfc8TEvyNmHDnx5j0xN3EjJaMCJ5geC1YeEYcfzGZnr/9/kMvWImdiis5gKVnqeKfWrj147nVG9KE9AENIFOJSB3cEvphQbRTZGzLCwfy5ALr6dy3msMu/4OIoW91X1fZDAx0kMi7bAMoER8fcsi5XtseuQ2Nj77MDE7TCqcF0jfiH+ZSkIqQZ8J1zD8/JvUSZEegKIpJ+rietEENAFNQBPo+gTU3bz1li6qX1LqUPKFCfT5rwmYhq06Q0iKYzrd9Q/RAIrDK8ouFl68hg/unULNy38gnJtDPBTCknIGLPxEQnmBgy6ezuCvXaK8RGU0ZT5UZYOqrXT9M69HoAloApqAJqAIBAZO+gdKNaAteib4SgrTa21efpgzb+3I+aANoLi2+K5S+W7as5UVP51E7aJXMfK6qeTNkONjY9OcqCUczqf86jspOePLrWAC2TN5BJAdK2HVdhyM3pQmoAloAprAkSdgGOLpiSlszROx5Of0kzU5aAMoVh3DpHrNe6z+6Q2qiW0otxjXdFSZA6ZNY1Md0W49GT1pDgXHnr73bLQZvOAJIfh375v6B01AE9AENIEMISCNW2UobXf94Od0G9xBG0DJWWnesYVF0y+Dqq043fLJcsDyxbqbNDXWUTBgGMMn/5yCASNw/RRWmkx4phv8Ax1PPB5Xb7f9f6B19XuagCagCWgCB0/goIOx4tBmF3en5PSzkSzQUMrHM0wlfpqs3UP3ivGccNsvlfGTLoASA9bLwRMYM2YM48eP59hjjz34D+tPaAKagCagCXwiAcOXlMyDWXxXqX3jJlg+6zq2vvEsOdlZxJvilJz1DYZdfgd2NCetMn0OZnjpuK6cIlHX0YsmoAloAppA+xE4aAMo5lJq/xzLxGuqZvGU71G/5C0GTriZQRdMCgyf66rawPY7TL0lTUAT0AQ0AU2gfQkcvAGUaU3VykJ+MGjY+AE1a1fR/6xz1JEpb0XMoHZY2vdM6a1pApqAJqAJtCuBgzaA++xdvEFt6/ZBon/RBDQBTUAT6BoEDi9DxRAZ60D0xUbmqQ46p6ZrUNJHqQloApqAJpBxBA7LAEr2jC1eoEwM6pBnxl0cekCagCagCWQygcMLgWYyGT02TUAT0AQ0gYwmoGOWGX169eA0AU1AE9AE9kdAG8D9kdGvawKagCagCWQ0AW0AM/r06sFpApqAJqAJ7I+ANoD7I6Nf1wQ0AU1AE8hoAtoAZvTp1YPTBDQBTUAT2B8BbQD3R0a/rgloApqAJpDRBLQBzOjTqwenCWgCmoAmsD8C2gDuj4x+XRPQBDQBTSCjCWgDmNGnVw9OE9AENAFNYH8EtAHcHxn9uiagCWgCmkBGE/j/KczIOqtcDY8AAAAASUVORK5CYII= />
  1.go to the right.
  2.go to the left.
  3.remain at point A.
  4.oscillate around point B."


Related Topics

Need homework help now?

Ask unlimited questions for free

Ask a Question
Marked as best answer by a Subject Expert

djpooyouma

  • Sr. Member
  • ****
  • Posts: 325
Reply #1 on: Jul 28, 2018
Answer to Question 1



Answer to Question 2

2


imowrer

  • Member
  • Posts: 514
Reply 2 on: Jul 28, 2018
YES! Correct, THANKS for helping me on my review

Hdosisshsbshs

  • Member
  • Posts: 315
Reply 3 on: Yesterday
Gracias!

« previous next »
 

Did you know?

The highest suicide rate in the United States is among people ages 65 years and older. Almost 15% of people in this age group commit suicide every year.

Did you know?

Certain rare plants containing cyanide include apricot pits and a type of potato called cassava. Fortunately, only chronic or massive ingestion of any of these plants can lead to serious poisoning.

Did you know?

The first war in which wide-scale use of anesthetics occurred was the Civil War, and 80% of all wounds were in the extremities.

Did you know?

Dogs have been used in studies to detect various cancers in human subjects. They have been trained to sniff breath samples from humans that were collected by having them breathe into special tubes. These people included 55 lung cancer patients, 31 breast cancer patients, and 83 cancer-free patients. The dogs detected 54 of the 55 lung cancer patients as having cancer, detected 28 of the 31 breast cancer patients, and gave only three false-positive results (detecting cancer in people who didn't have it).

Did you know?

For about 100 years, scientists thought that peptic ulcers were caused by stress, spicy food, and alcohol. Later, researchers added stomach acid to the list of causes and began treating ulcers with antacids. Now it is known that peptic ulcers are predominantly caused by Helicobacter pylori, a spiral-shaped bacterium that normally exist in the stomach.

Herbivore biomass is positively correlated with net aboveground primary production. Herbivore biomass is positively correlated with net aboveground primary production.
Attributed to the Manner of Peleus Painter, Red-figure calyx-krater. Attributed to the Manner of Peleus Painter, Red-figure calyx-krater.
How to evaluate and sketch a piecewise function (Part 1) How to evaluate and sketch a piecewise function (Part 1)
Let f(x)=log10(bottom exponent)x. For each function g(x) i), iii), v Let f(x)=log10(bottom exponent)x. For each function g(x) i), iii), v
Finding the graph of a Parabola using certain values Finding the graph of a Parabola using certain values
Position effect variegation of eye color in Drosophila Position effect variegation of eye color in Drosophila
Video: Glucose Evaluation Procedure

For a complete list of videos, visit our video library