This topic contains a solution. Click here to go to the answer
« previous next »

Author Question: A vertical cylinder with a movable cap is cooled. The process corresponding to this is: 1.C-B ... (Read 32 times)

schs14

  • Hero Member
  • *****
  • Posts: 569
on: Jul 28, 2018
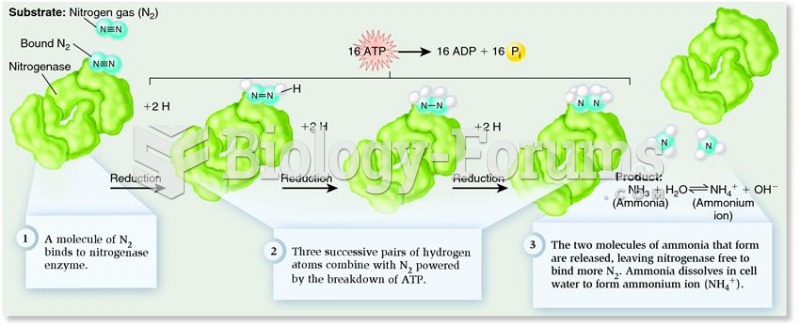
A vertical cylinder with a movable cap is cooled. The process corresponding to this is:
 
Question 2

sDDYn3322YUwCY+Fv/knuuqqqwpPyBwTHXNZJGTNSSJLUt2f/OQnRWb08Lrhb3Cw2JtUQAjiVMHLExwsPk8VwqZhls1NIouQwSMzJ2QZpgRw5EwmEzYNHJh9UwXhR3JfsCCIU/OXqfb8uDPgDPQeA4yrfBgnEXa2jNZ6zNrMnjHhhzMLSVNjzhP25vnOmwEmSAZ6u24vrKe/NYnsSiutpLtKt3iGknXRgPCAAAAObUlEQVQiBwcaDk4dmApzcKBJcp8pZxzAoXkSnSXl5ENdvCsJUo3TDF6iqfK+972v0LBzcKB5gsOuvSxrnyUmO++8c9E/aOOezLaMKd/vDDgDKQaY6sLMyRbLGsXOAabOr/N4bWbPjTfeuBBeJJFNmSwJa3bttdcWSWFjGRvsDZJmBy2MZQrbbLONPTToOwL4/PPPL0KsIcBSwov8g+TcI3lrKqkujjfgIGsE2Q2qCtoSONAcEWAp4UW+PbCAI5WZnrWTrJvBMzQnqe65555bCCxwpPoFTZC++dCHPhT1JPVktlW93jvHrAmLt/lOLd2Cs1P5Gw6uHO5z6gwHQ+rc2sye//jHP4pEsgRNThWWGGD6w/yWKnhLIqBoP6dghiRDO5pbqrDEAByYI1OFpQ4Ih7vuuitVtVDvFQeaW6qwxAAczMWlCksdeHHIwcHLAG9VCLScfknh6OSBLsWbH3cGnIGRY4AlDFpiZk38GUa71Gb2RNNirZ8N8cXNMQAj4a2UR0tE08IMaIuaTjE9asFER7SVsF21Idu2+b7XXnsVocnCYNoxHJtsskmxLvENb3iDXq7YxnDgAUng7lCbjOHAZIljCNFRbP1YXS6IQwvrEnNwLL/88sVSB5Lq2hJrG5MluQBZ52f5i9Wlrc0337wIBhB61iofnGf70V7fvzsDzoAzoAxg1lRzJnKBol6dCD41ebIfb/7RKLWZPXG2IO6jLSyYJmQZJjpS4VQVBtbvfe97RbzOfffdd1AmiPBcPBDJhoDQJdJLVUHTZA0iAvdTn/pUVdUi5ig4CG3GfGWYgSE8mbBihDgjWe+73vWu8HDTbzQrcLCkADNkVUFgEWYNzRc+rBCNnUdiX5Lqcn+aVDdWj31MOpNUF7wkA64qCHDWCfJCgjn0wAMPlMsuu8y9PatIG+PH7AsQ/7edWroFZ6fyNxxcON7lRNTiGoxHOcvehoMndu4cFSt2tIV9qh3YUxg4MSnaGJn2uP3OPxERRDD9MWeWKsynMR+Y44CByU8Tw6ba5ThzW+3AoXzYNEdleFrlAyEJHznmXvigX3JwgA+vXfqGPrZaeRl23+8MOAO9zQDCLPTqjDEyWoIPLLVpfpgmMTmioegAyWCP4COsljXTIbDw6sQRxLrOP/fcc4Xgw2SpsULRgDTOpnUcYTkEApB27QJu6iI82W9x0DbXagcOsHDfIQ6ERcgHOKhnNTm4gBPLB8KPurTBQn+9lyo+Qhy0AR9sW8GBiVRDoSkOHhau7clsY//CvbWvWzSqbsE5lp8eDaIfBhq3mR5G6/5r0/xYN8acmA3nRSBklhdYgcONYp7be++9ByWzRegRO1MFH3UxWWJqo31b8FwkHqcVOAgKTSKL9qYFHERGCXFgKgRHmMw2hgPnGLImsF7QFnDQtsWBkFAcVrtSHFbw0RbmW+bm1EbOPv5xEXrwoYKP/bwpsUzhpz/9qYVReHLGcJBq6ogjjhjUL9QNcbDOEhxhMltw8KFfcrTyJmD+wxlwBnqWATRAvNN5ibYfm+lhtMipTfihtSBc7NtW2U0RrQQBY7W+sro4bVDXan1lddnPgA4OKzDK6g8FR2q5ANeCA7Qn5gtb4UO1rTK87Fc+WsHRSr8g5Mpw5NxLFXY/5gyMJAN2sG3ndfm/CD85wSbARL3wXP8/a2dvzWm7NrPnd77zncJBxGptzD+huSG4rGcnGhofBJQVUtRlPgqPRrQkCg8w2gYPhG2beSgitxA6zWp01OUchIQWTIoEhC7DQbv6wHEuONDeCP+VwgEGsHB/VpMqw0Hb1AO3FuWjDAd86P2U8dEKDsys8JGLA60XftBuPZmt9lrvbvV/BQZ4Hnu9EPM3NOsdfPDBRQLXFDcsA1BvSK07mpkOFEPuFuEdJqfFpIknvXp35rY10vVq1fyscOJGWJD91a9+Vc4555ym+0LgMZhbwYcAwBOSrALWQYZ/NOqGbRN/E3NomA6Deioo9KIIHJLqhqZCxWH/mcGBh2osmW0MBybcgw46qMlUyHVjOBAi4GABvC0xHAjfsmS2MRx4nIIjTGYbw8EDCw5MD7bEcDBv+93vfteT2Vqi/LszYBhgoA9L7jq22Bq4Thcaeq/cIx6ddrqGY7wIINBj96bndsK2NuEXCiduDk2LwMmpvHPURQARqoxlCznmUNbEEVqMuatUwQS59tprZ+Mg6gzJXnNwsP6PYNI5SXUVB1FiUgVBRLYHcJSZIW0breBAU4aPnCTD4GBpBljQghHKXpwBZ2AOAzFhFQqEObWbv8XqxdprPqszflnhhqaLFcB6eIYabWegnoOiNrMnGR0wibHGLDVYo4nhuEEcylR8SbwVccBAuKRCkEE+kVUwt2I6sE4oc255zjc0MbQgQoql4m22ggPtEcxEdwFHSoiCASzcXyqpLlox2h1CPxUKDRzwgfYGjlS/KA5eQmIvFSx3IP4q2q7IsiKyj4gQW5WchWXmr7lFhADhp4vI7+eQ3//NzWaDKOn4HdZS4v3X6C5eUkNBlspWwP9buBZuOCZPXTw+nDZaefjKnoOy/coRZtHQ6tTKdeuqW5vmR9R/ErjmhNG6+eab5dhjj80KWcZcFmY3PBFTBdIxKbKAO2f9H2G/wHHPPfekmi7W/eHBefXVVyfroi2dd955xVtQzro7wrGB49577022zXrFE088UVhcnyrgwOTMG1pOv5Bk+LjjjpP77rsv2jTmVtr04gw4A80MxLQ1hFtVsZqT1ouZUPVYaqtRU44++uhU1VqO8+KjH23Q3hPaoC2KC7NorlnYnl/39zleIcNsGeJzgjhzGcyEaGWpSCTUJVcf6nMY+qsMLm8VrHfDQzRV1ltvvWKJgCZxraqPy+6ee+4pZYlew3OZBMaxxDrjhHX0NxkZqIdpMVUwVYIDJ5icQqDx3MwQ66+/fsFbWbBxzNjhfGoOBq/jDIx1BhB+oZnvmGOOqXR6iQmAmBDN4e6QQw4ZqDYcATrQyBC+WI0v5vADLrRSNGTwhv4aQ7jksE6pzexJx5NlgIXnKVMIZkCWGSAcUhoJc4kMupjuqJ8q1EU7AQdmv6qCAObTCTjgBBzcZ1VB+LDMoRU+eChz+gUuqnCwhvPUU08VEue62bOql8b2MTvIpf7XxzYTzXenZj27tyyCSd0mT+2TlKnVYqv7u2LQdmNY0Az1JYEQlaMlqME4TM1vThgyFn+TPkdd/JWA2BbhhFCjbkpAQSgDPvWoX1Woq443OTioCxbH0WA1h485LysI6bJ5vqpe8mPOwNhkIKb9od3FtLmY1jdUQWC1vti1YNsKJl5YOAfNVIsVVHbpBpoabZa1q+ezDdtFyIXn8VuFH4JwqPdsrzvU78PU/C4QkXOHem0/r6sZWEJEDhQRTLUvVghCd3jp6m6OgA8H0kiVntzVijZnBYySVaYl6vGyrfZHlaOL1qENTJJW8Gm7CEAEUui4w/FWtDR7rZhlwGrIseOKp93bIQq/CSKC48PtIvLXdmP09juSgQWZvRURhCA5HMu0QBd+Hdl9DqotDNiBXS8QG+CtgKiqp8fKtlbgxubZ9LzY9fRYzjYmWG2b9h7L9ut1rNZpNU49PlLbIZo9MT/yeWe/q/tIwfXrdBYDPAPpZL2dhdnROAPtYwAzXqg5YeK05r2YF2joGZmL0HpX2mtUnW+XGoQaKEJO427aY+E90T51dT8CDW9Oa4LlOrECTtU8Y1zEzmnHviFqfgoFDXCI8lOb8G2XMoCmx7wfTkU8RmXFNb8yZnz/2GPAamJ6d6FGZjUfrdOKWVHPYWs1zSqzqdXGbL0Qb4jDnme1O66NUNflFRaTfg/r6357zZhGqfXavR2m8Gs3PG+/+xlw4df9feh30AoDVmBwXjjAW4Gl7ZYJCj1etrVtVbVhMYX1hnoMTAhAhLlqgOxD40MLrEpQW3XNsnute7+vWK6bUW/PGXAGepqB0ISJYLDmPSsoICqs3wp5YVutnFtHXUyYrNdDoOpHzaZ1tN/ONlz4tZNdb9sZcAZ6joHY3JsKPztHp8TE6usx37aPARd+7ePWW3YGnIEeZCAmzFTo1bm+rweprfWWXfjVSqc35gw4A85AY97L8qD5/nSrx8o8IvW4b9vHgAu/9nHrLTsDzkCPMhBGNoGGdmh9ONNoibWvxzppa3Fa/CON0YXfSDPu13MGnIExz0DM9BlbFhATkq2QE7tOK+ePRl2d/+Tao4nfhd9o9L5f0xlwBsY8AymTZup4DkF2OYHVqHLOHa06LvxGi3m/rjPgDDgDI8BASqtJHc+BaDXHbhF+FmcdHOTwFKvjml+MFd/nDDgDzsAwGbCCKdZU6njsnNg+XSdYteZP1+CFC9xpb6jHYlhy9inOOjTfnOuV1XHhV8aM73cGnAFnYJgMlDl0lO0fyuWsENUlFUNpZyTOsfg0s/tIXDd2DRd+MVZ8nzPgDDgDNTBgBZNtrmy/rZP7nXk/1f6scMk9fyTrKT6Ev52vHEkMei2P7alM+LZNDHhszzYR6812CQM2jqVCjpkf9dhQtjiRrLjiisWpYXDqobTXjnOY61OP107A6JpfO3rZ23QGnAFnoJ8BO6em3+smBy0KgUKxaYXqvs5w2lNcaKmj6eii9+D5iJQJ3zoDzoAz0MUMIFDq1ijrpIMA2J1UXPPrpN5wLM6AM+AMOAMjwoALvxGh2S/iDDgDzoAz0EkMuPDrpN5wLM6AM+AMOAMjwkAw54fz5xQRmU9EkIuvjwgIv8hYZmCe/pubNJZv0u/NGXAGuoyBQPjNFpFnReQhEXnFhV+XdWZnwmWpw8v9n85E6KicAWeg9xgI1vmh7b1RRBbpF3x9vceI33HNDEwQkVki8nD/i1Vz853sndaM1H85A87AWGIgEH5j6db8XrqBARd+3dBLjtEZGHsMuMPL2OtTvyNnwBlwBpyBBAP/D15Rrn6F3NgWAAAAAElFTkSuQmCC />
  1.C-B
  2.A-B
  3.A-C
  4.C-A
  5.not shown"


Related Topics

Need homework help now?

Ask unlimited questions for free

Ask a Question
Marked as best answer by a Subject Expert

cici

  • Sr. Member
  • ****
  • Posts: 325
Reply #1 on: Jul 28, 2018
Answer to Question 1



Answer to Question 2

4


schs14

  • Member
  • Posts: 569
Reply 2 on: Jul 28, 2018
Thanks for the timely response, appreciate it

Dinolord

  • Member
  • Posts: 313
Reply 3 on: Yesterday
Great answer, keep it coming :)

« previous next »
 

Did you know?

Though newer “smart” infusion pumps are increasingly becoming more sophisticated, they cannot prevent all programming and administration errors. Health care professionals that use smart infusion pumps must still practice the rights of medication administration and have other professionals double-check all high-risk infusions.

Did you know?

For about 100 years, scientists thought that peptic ulcers were caused by stress, spicy food, and alcohol. Later, researchers added stomach acid to the list of causes and began treating ulcers with antacids. Now it is known that peptic ulcers are predominantly caused by Helicobacter pylori, a spiral-shaped bacterium that normally exist in the stomach.

Did you know?

Certain rare plants containing cyanide include apricot pits and a type of potato called cassava. Fortunately, only chronic or massive ingestion of any of these plants can lead to serious poisoning.

Did you know?

Most strokes are caused when blood clots move to a blood vessel in the brain and block blood flow to that area. Thrombolytic therapy can be used to dissolve the clot quickly. If given within 3 hours of the first stroke symptoms, this therapy can help limit stroke damage and disability.

Did you know?

In the United States, congenital cytomegalovirus causes one child to become disabled almost every hour. CMV is the leading preventable viral cause of development disability in newborns. These disabilities include hearing or vision loss, and cerebral palsy.

The formation of gametes by the process of meiosis is known as gametogenesis. The formation of gametes by the process of meiosis is known as gametogenesis.
The process of placing a stent in a blood vessel. (A) A catheter is used to place a collapsed stent The process of placing a stent in a blood vessel. (A) A catheter is used to place a collapsed stent
After all valves have been properly measured and adjusted as necessary, start the reassembly process ... After all valves have been properly measured and adjusted as necessary, start the reassembly process ...
In this design, the fuel injector is at the top of the cylinder and sprays fuel into the cavity of ... In this design, the fuel injector is at the top of the cylinder and sprays fuel into the cavity of ...
Thermodynamic Diagrams and Vertical Temperature Profiles Thermodynamic Diagrams and Vertical Temperature Profiles
The Process of Sperm Formation The Process of Sperm Formation
Video: ATPase function - membrane transport, contractile proteins and synthesis

For a complete list of videos, visit our video library