This topic contains a solution. Click here to go to the answer
« previous next »

Author Question: The circles in the picture below are Gaussian surfaces. All other lines are electric field lines. ... (Read 312 times)

SO00

  • Hero Member
  • *****
  • Posts: 568
on: Jul 28, 2018
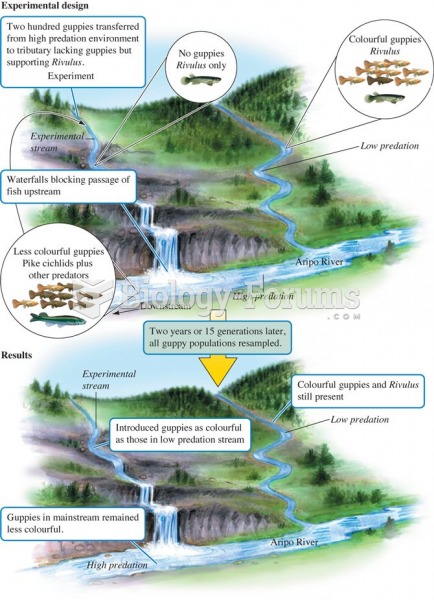
The circles in the picture below are Gaussian surfaces. All other lines are electric field lines. For which cases is the flux non-zero?
 
Question 2

IHSYHYjdsNN06tBE7hJ4vvKElpQcS+h5JuVeW/BhZ/taeHQoH38oZwPIiazT2YxM+/bsjd3Vo9b4bV/bQ77HTvO4YZt0diXVxGmxRilfjTRzyJ7j2/VMWeJ0SbcV+nJC/IB+PFfdVhFv6k553nvdFs4a7myDDR8Q9uHhfHDZB4Z9fNzeR4fLDy/76PGhFR9Bzsec7dG+7xL5kaGPs9vnQ9P7pg3+tg9lR4b5uHToRTsZ23yM2oepfVS+/Dh96uC11Ef4Vxd85/nANlgGMBjBAAAd/ElEQVSu5Y8H4MuH7NVTtLO5ji7HCnsNzNQJ/WmbenSBJvBLW079KXu876vgawqtS93VTuW1qz9aaLODIbuOT2trq/2Zj+Tj86V9x8fYEhjx3bLOXMdgl3wkLswFf5dwji1UylSnxSR6JV//+tePJXMjAS/Nj5lOO9ZwiycZaUCht2bhyr5KpnqN2oyM9OL1LCPXfdFV4+0bKadnap+RXzkTAJbRvSl8PNbTfrfffnszKtXGlmn/cpSXxwp5TuncKFlP3zPYFI8hrrvuutVXv/rV1Y9//OOjZ7ba2fRs6w+UlNM3euRmLWyu048RUka6wTN2b5HHvop3hPGxr1KPUNeVYU0//y3t66SOWM167bOQmyLW5NEV31Pi05Fz9s3N//xkxi5rFEo4gWF1/W233TbLLF6J2zHYodO5uHJiiwyekYuegh5LejPu6YGVvd5D6kHUvZuMZHbZKyE7Ixi4jYb0Al1T0jPMTMA+6OuSBdpKvY45Zh/sAT99hTxKeKXNOHYv12J7OQcfbSlkmnt61NpGjkaw7gcX+tQZKuqU7dK+bz8W9hDuk3ifTvAf+bDxuQr9l7BL3c+F4zTB6fNbcmTX/IPP0JsYyU/YvPOMUsGxqV/KPzru2gdH2gce2PwevrZRb58ODiGO99E39d6x/1MlyAiG8BLMygDkOoG6R1FJIFMRz1EfDaXyGc8uCp7JiUHFuNBSJpskWQaTJDNnMNqETzShu5Td0LH6Q/IFF9+xkdJuYi+lXeEhstFW4ZxwpZCZNrEzNuc8eEI3+LlmH3iBU+9Da9qP2YevWtc17NN0Tu6lHslgSLZT+afjUv5sYCntEpjqt+SqDRnztTJGBQMd8233beratFsHHxuJrwQ3eEm8fLhMvPw1+tcuvh76Ttr+KKmWAQkThByBCCJh2j4BzH3tIrAIaxdCoZTS2dGxjYIXQYSx4RuvcEU2eC5L5KZOgo9jcttHsCAnNMIdR2G4pT77jtXVrs0Zwzee1aEPcgmfSVwlPvXKok2pO23BSAFD+8B0PfJEt7qlDtQD0wZXdBB49Z5O1e2TQds9eHZh5zW9uz4n25L/Uldz0cJ+Shuh07Mg23XkRzalPupjcrTFB0q5pq579Mj22TH598mbH6WtfeKg6+DY0FXibMNbwgiNNT/O0WRjezY+LP700biOLLfV5iipElQEQ8gKJgiOAEohqZeCYYyrl/b22VyXkMDsC8yBN3YPbpSEtqHgOQYuftGY3lppLI7hxGsXHwnQDCIlAYM8tN12QVv0geZSb5HX2D2aYwsl3XC4js/gULfku6yvTnCihxzpi5xr3YEBVlnU57CRL1jOtQW7rYCdOtr3FbSUNIbWco8m8HINbufaobnLJvrwnoR7eAvP9uS6jUK+wUO2p1Wem8qulFPkZU9m9bm67JPf2Duv66WN6+7zFTqv42npH+y+LS7gLTE0MYK9wA+uDY4+OkJPvUcfvGkfeGiFA71wHoLdNK/UeCCc98fygLr8gILFBN4LzMIV9bPIpH6Y3PaPJOWrCha4wJGPo3ct867hlufoKT800EVL2SbHeU8zr/T4ZwR/Z5eH+3m3NjTWH3IInHKfd/e0feSRR44trc9CJfC39amv8h9X0FDqqaQzxxZ05TWfcnFA7lu0kNdeLLf//e9/33wA36sQZF/iSN2ur+OUi5Ly37IWSqAhr7uQWb7i5NURH3bw6owvVfmIiFdpsrhCOwukbrjhhobP/GE5G6gL2n1cwEcK2J1XcPpee+AD5cKnwLMIhD/kXVbXLVryelT+5SYLPCwm8noFu65fXQi8k7T3GlQWJdH1tt6zLvGQD33v6/WlQ9aPd/LFkvhDaOUXFvspFiiVfk1vXknzrri/pFTYeu3LzY3iB0y27DUon5f09Sz+rICZ/zUumow+BKf8eEj5aha6FHFGjCh56UOAJiXfQcjCPnzwxfKVwW365lFSFZh9kF2As+KyTg4ClG+dlkL1bdW+IIXBvAMl0PuakGCpMAxCS4lBSGZ1YQwphFEGPoLMPy2kjv/FLEsSpmtRVAQffDE4Hwvo+5hDCZfM/OG21b6Mz8rXcmUt45BsBHYrqiWH8n4Ja5NjDpLVf21w4nD1F5Q4aPSZdnFA7x4OOR2cfYkKbDjqTk/k5j7aUthA9CNJpcQ23Pvtb3+by80ejTpYnLItsaqUTo9gQ++cLe/nals6mMTp35hKuQwF+CTbfDginYXT8LWgMtmxDbrbhg2XeOhsSObHjOAMneikK3xZh65MrvFdA5a2d4G142/5xGeSDf8o/zWqK5GpX3fYdbj8scTYN0LYT/mNbjR1+W5yh/dHda6VJFzfIUgOQa8yJvmSkVLGf7EObzocScRNpTV/jpIqBowkBAI9cKO3OkilTgSLEB9xHyvQmsaMGl3P15kycnQNsxFe2pZG5FpbMpEo0zYCU1fw9CL0ph93iGF4PUMytbV1LjgAJelxS6q1PMPTpvt8RCFwGE6SB9xxntzPnjOVL3jnuvZDBtrlCIHRlVBzX7LVGZEk2QGb8jEQe3KVrKMregutbR25MYkV3jpwuxZZxWboSxJHg9dIyLGctQn9fXu06gCgf13fqOEHZn192+c6CulgkJWAWHZC5sJf4gFTsJ4jwM1F3xCcOXXdh0tMEQP5NB8xY8Kuy7hIT/mkJ1g63ew5cTvwwZBgDSjykRb3xDfx2OCk7aMuaZ89OGKg5No2IJE3zHahoaRDO3oucQfm2H1b4v3DH/7QdCqSO9JRB7MvrqGlfCVvLA3n1Cvn+DOnbl7ccdszQPPX5Xy3uW7z7ea4zbNru60CR4nb+a4KvvCO1zxL63qugKY8/3Oc+f9t0YqO4EDjlOcKtUxL+XYds42+wm60JYO24vmH+2iti2td8PNMpW7jPDiHbKJ8NtTFX57fxLbxga5t2nYbT+U1Mumid7m+2w89tMm7zZZL/c11XNsve+dPYkB9D52J42ICGhO/ah5i623rA9KWH4DHD+v2zuM3cCQeOa5tN7jq57ZzyaiGw2/xYBMnyAEvaAx9aByKHTXcrvOjkapsq0dqSkHPXO9Hr6Kebks9I42y6B0ppu0yepvzuVJGPsFppLSt6dTg0AvKX7dlKjS8tY1M005PTy/MBwv0tsmq7g2m7r73eCw/DzZED776Zif0ij/+8Y833+vt6vVllNr2ycY8U20bHWaa23RP2wgwI9Z6urnmKb39+nrfOb7bfKGvzZz3+GOmvuaEOwRLL78c4ZBDpuOH2k65X4+0Mj03BcY+67L1XYysxZYf/OAHx55H0olRq1kpMxoej9XPVc3oeXynDp83M5CRaKlfMgQvU8T5F6hStplZyozmmNFs2ovb/hRjF7IKzrF7sm2LK2PbH9Urs63ejl6IjK4ki5d1cizblz0WmV72T2+m7LW09X4CZ2iPFnSkZwQuHNso6cmUPRi44dPDGTNS0fsil9AIJpp31StbRy4Z5UXGXXt8tfHhWvSubV+PT13yYBNtxXW21FXQQCddhV2C31cHDaVNdfFbXu/jqYuW03A9+oos+nSzLr90Fvj2fbpbF8dpaccOxRR6oYtSbs4ze2Zf+mTqqUO+2qfw/9TlO6lrz9+0cR/MrhgIHj3yXzRqo20JyzH4gale4OLptJSjV2rCEIYT8AjQeVdAqRWbYKmdewmQtSBdL5Ua3PW+TtxoYQBzlJLG0gjgYHRR9lRcMdq0iwy6jDH19r1Hd+0A5TkdxmFDK0cgO/dSl9z6Sup31Ym8uu4nAPfZT+r0BWe003Xo7tu38d5F32m8To6lfMh3zlLbXm1nc+I66bDIypYkxF9K


Related Topics

Need homework help now?

Ask unlimited questions for free

Ask a Question
Marked as best answer by a Subject Expert

234sdffa

  • Sr. Member
  • ****
  • Posts: 341
Reply #1 on: Jul 28, 2018
Answer to Question 1



Answer to Question 2



SO00

  • Hero Member
  • *****
  • Posts: 568
Reply #2 on: Jul 28, 2018
Both answers were spot on, thank you once again


234sdffa

  • Sr. Member
  • ****
  • Posts: 341
Reply #3 on: Jul 28, 2018
Great! Please up vote :D


« previous next »
 

Did you know?

Never take aspirin without food because it is likely to irritate your stomach. Never give aspirin to children under age 12. Overdoses of aspirin have the potential to cause deafness.

Did you know?

The term pharmacology is derived from the Greek words pharmakon("claim, medicine, poison, or remedy") and logos ("study").

Did you know?

Though methadone is often used to treat dependency on other opioids, the drug itself can be abused. Crushing or snorting methadone can achieve the opiate "rush" desired by addicts. Improper use such as these can lead to a dangerous dependency on methadone. This drug now accounts for nearly one-third of opioid-related deaths.

Did you know?

Approximately one in four people diagnosed with diabetes will develop foot problems. Of these, about one-third will require lower extremity amputation.

Did you know?

ACTH levels are normally highest in the early morning (between 6 and 8 A.M.) and lowest in the evening (between 6 and 11 P.M.). Therefore, a doctor who suspects abnormal levels looks for low ACTH in the morning and high ACTH in the evening.

Four Concentric Circles Four Concentric Circles
Field horsetail Field horsetail
Big Picture of the Evolution of the Universe Big Picture of the Evolution of the Universe
Damage to Field CA1 Caused by Anoxia Damage to Field CA1 Caused by Anoxia
Optical microscopes are commonly configured for bright-field (transmitted), phas Optical microscopes are commonly configured for bright-field (transmitted), phas
Gland #2 (Soft) Picture 1 Gland #2 (Soft) Picture 1
Video: Gastrulation: cross section of the frog

For a complete list of videos, visit our video library