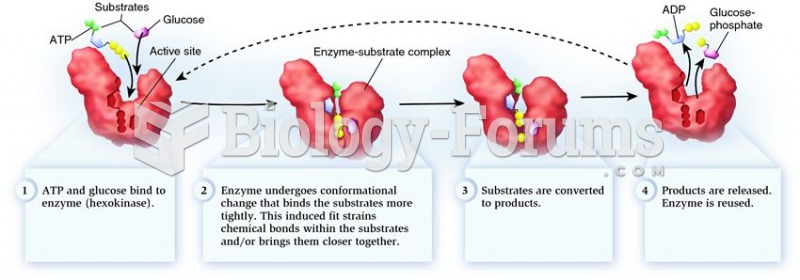
In the reaction shown below, what are the molecules indicated as X and Y?
 Question 2
Question 2ySg8aOEbtUE47DIXh2GzmzJnl8fTp057Sax68BtCh7N27V2Z4nOQrVKiQwNN2+Omrn9JMiu8rfVKklQqwVBiVqxV8YP9+M23qNDNr1ixz+PBhOTHVt08f06hp9Dtiw8aNzdw5c8ykyZPN4489ZiIjI80DDzxgmt3e3Gs4LluBo4qblpbD8clF64DDNdRLMIVHbtppqwzdOuTYLk7d05ivAAAgAElEQVTpKYzru/AoNT9c9uzZveO/jPws7k2dOlVOBPKah2MmwprBo48+akqUKCG8qOILQFL/Eljd95NTSQLulg8kObDxxowZttaNNW3mTFfYGjdUs1MnT7FHfz8am2P0zpI8f7d1m33koYdt4QIFbc7sOWynjnd7+7yxCH4olATcOjh58qStVasWUyVbtWpVe/z48VCokubic1CnQoUKgn/zzTeH3G5TPHzcpk2bbNasWQV38ODBXr6TJk2SOLb0oMm+/6233mqvuOIKib/pppvsjz/+KPC6feghJyFAr+G7iyyBZcuWycmtiPAIW6JYcfv0kKfs3j17PC5oHO4JKy/BWrvi4xX2jrbtbK4cOW3xYsXtoMGD7Y4dOzyQlDQGj8i/NIBc9UcRUSqUPk+ePJaDMzhVzPhE4OIi55YtWwp+kSJF7O7du+ND8eJc3OnTpwseJ/OmTZvmwXDar0OHDnb9+vVeHHhLly61BQoUEJxhw4Z5ackN+EqfXMklA4+G1bdvX6nAvHny2m5du9rNGzfFUmIgiBndaVRuQ9F4gE+fOmXfnPmmrVO7tg0PC7OVK1WyE8ZPkGOiscRiQjGjy9/i01iEK0s9BMNRWJSe3yuvvBJSIlofAGnHOmLECMFNnz69nTlzZkh8N7F9+/aClzdvXrtlyxZJgiel68JqeOjQoYJTs2bNkKf+FD6U7yt9KOkkIk1HZEC14qL+irI2KnZufvDAQTt65ChbtnQZGxEWbhs3bGQXvrfQnndgEpHV30AOHzpkRz//gi13TWmbLSzcNm3YyC6JXBRnqnmeziMqdoRzGy+K8G90rvK4yq5l1XL/8MMP3pn7MmXK2L179wqI4ri+1i0+PxxHeHPnzi3KWLduXXllI96VsYYVZ/Xq1TZnzpyC065dO29moXkJ4QAaxM2fP19wihYtag8ePChgWg7FSazvK31iJRUPHEKnUt2fVESMLp05fca+9eYsW6dWbXlvr1wxekT+5Zdf4qGW/Kit33xr+/fuYwvly2/z585ju3ftZjd+vtEjGHUuuqHy0Yg2XnjWhugB/gsCqjyqEOpTNI7NBrrnn39elInRvm3btva3337zQBRXFddLsNYiS9zAgQM9/CeffNIDUVz1SaDe69WrJ/A5cuSwdAA4YPRHXhrn+swk4LFy5cr22LFjApPcP1/pkyu5mMpS5dHKUnKrPllp7+pwp82dI5ctUbSYffyxx+zOHTs1ObqS3Tm7l5KEACN1TAfDaL50yVLbollzmzU8wl5z1dV26FNP2z3OuyY86k8bWRJyuyxAtVz46g4dOmSHDx9umzdvbr/99luNljpAgRhxdZpfv359u3jxYvnCzgN0At999509fPiw4BJ94MABW7t2bcHnHZ0v9HSxzUGzGzdutI0bN/bygR8cfGqdKLyWgXjtmHv16iW4PXr08PJW+KT6vtInVWIB8FppGk2jGPDwI7Zo4SI2R7bstuOdd9nVK6N7dGBoilHnz9uzfAqpSCnwAxsMjXjG9On2xuo1bJYrMtvqVW+w06ZOjTM6aKNKQbaXBeqZM2fkAxcUOUuWLLLavnLlSk/RkAOO0b1z586eQrJ6zsp+79697ciRI+2oUaNs//79bevWrW3hwoXtmDFjBE8VcufOnd4ITudx3XXX2T59+sg6wQsvvCCLc7ly5RL6GTJksM8884w9e/as0KD+cFonPGtY+eO9P1++fDY8PNzCP07x5CGJf77SJ1FgwcAZTVgMYhsnLHMWe1PdenbeO+/Kd9XgiLLb8zbK+3mDdDCSCcarwuuUXRsJiPv27LXPDnvGlrqypM0WkdW2uL2FjGDaUBMkfpkDrF271nbs2FHeuVldf/TRRy0dMjLS1xzCqjzIhW/e2SrLnDmz1wHoDEB9OgQW1QId79mPP/64LV68eFDcW265Rd7NXVxVcvXhSX/AsbXYtGlTodmzZ08Z+UlPST165rL00Aj7/KEOGbjnANwDC4TdD0OgoekuPeKCpbm0Uxp289ZwIE2Xr8A0nsHjp+UiDI6Ld/bsWbP4/UgzYfx489mGDXIGu2v37qZTp04mX/58fyNL7eFCm1+MAUrA03KFkueWLVvMq2PHmvffW2gyZsxg2rRpa/r27WvKlb8uDnWtfy2blpV4wqHMMMUhdIEe4IGfWxdyopHjzOljpfn9zu/N9GnTzMyZM80ff/xhGjZqKFZq+IbBdVo+fJyWm5N2X3/9tfnyyy/lsBQfxVxxxRUmb968BlNZZcuWFYs4HNtVHJculnUwWMnXc7/++qt8YMOBmqpVq5rq1at7p/eQK2VRueuz8kMajgM5o0aNEtwFCxaYwoULJ3iQyOUn3jC9iY4UhLWXCeUHwvHs9lQ846Ch8eprXAzIBfE0D8pFWJ3Lgxuv6eqTpukadnEVbt3atbZrp842T/YctkiBgnZA/wft9m3bNDmOLL3IixSAbx0N8CMXLrQtmjSzEZmz2LJXX2NHjnjeHnC+/6Z8uKjz0dNLnrXMjIwqj4vE/t+ycfnxws7ux5FfjtjXxr5qq1SsLK81dWvXsf+dM9eePnX6b7RSI0Jlk1Raioc8Cats3XamNHWREeMeX3zxhURTl9quk1sn9BqaR5J9ZVwZhoBWiEvMhSNe4fEvhAtG3xW4Ci6+/AP5kmeH1d0/7LZPPvGkLV60mM0WntW2bdXarl65ioJ55JR+IC0P4AIGtPyUFz7UHTt61E6eOMlWrXK9zRYeYWvWuNHOmvmmPXXylILE2d5T3tX3gC5BAB4oCz/Kpe7cn2dt5PuRsg3Kdmi5suXs6NGjZbFNYVKTf2jpT+m7fnztn3RwXL41Dl/bips+duxYmdKzRcerisIrHbdeJTEJf+lYifzkk09kCuNO5Qi7TqeQnFPmM8TSpUt7yTpV4jwx05L4pj0KrNMYpa/TGE1PDV/5SYhWMDidYoEPnzq1PXHsuJn91lti8XTnjh2mYqXKpm//vqZFi5YmPCLmowssrAZMGaETSiYJ8ZnUdPh3yyZhk04+0oHWD7t2mSlTppq3Zs0yJ44fN7fccot56KGHTN36N3lZUW6tc/yLyb/HhBPQ8qhP0saNG83E8RPNggXzpf12aN/B3Nerh6lQoYKHmZx2pnm4voZVJmQQn0yAc9N4hgfVC/c5EFbpPffcc+app54yxYoVM7Nnz/as52qhlIa2S41PtL9hwwbpUXShIjG+rl5qr0Mn4/ZSGBTkaCg2wFatWmU3b95sf/75Z68vCtVTekCpEOB8NIs3n332meyJsgq6Z88ebzsGPuJzlMUtG73qe/Pn25ZNm9msWcLstdeUti8Mf87+/NNPHjo4Lp6WkbiU9MpeBkkIuHm7aPDiuvXrPrU9unW3ubNlt0ULFrIP9e1nt377Pw9E5aO+l3CJAxyqeerpp+yVxa+0EVnCbJtWre3yj5ZZORRFW5Qfi6aEz9u/zsctdyj2VXaBvotDmta1G69h0jRdZae+G690iMPxrEY22Y+n7QZzSi9Yeqj4dOwp8oUXjh4k2MhLGj0LC1fY765WrZqHQ4BeCvO/c+fONSw40Aur7W/SypUrZ2688UbTtWtX+ZJM81OffLVHFMLJ/GO28dFHH8nXaJgywtABCzo4PmnkE0UuHsC80R133BEnF8oYKIMvNm82r48fbyIXRhrWVlq3bmP69OltylesGAeXBx0dtcfW8gTG/w3xAkZQHhw8uWHNMurcX2ZRZKQZP2GCLECVKF7cdLv3XnP33XebAgULCJh8u58+nVc+pac0UsOHN5Wby6cbf+zoUfPuO++YiRMnmW1bt5pKlSqZnvffL/WoMy3gKXH6dOnizLhil/pCc6v5ub6L4fKoYTedMLg4lXl8Pm0CONU39Gr48OFmxIgRgtu+fXvTqFEjw5d2zK41Lz7n5Ys71T8BTupfqB4hVBo9jf6A+/LLL+PsVWbPnl1OD1WrVk32NnUGQby7TwluYO8XKt/ANHjQnnL79u2yJ8peqOaXP39+4eOGG26wLIjodoy77QI+o7HSIY+9e/ba4c88a68qWUqOzrZq2Uq2vM79FX0SC5iLPYIHlj01nzkt9uqrr9qKFSrazBkzWVkIm/tfe+Z09EKYytmt89TI36176Cl99YljsevDDz6wLTl4lDmLLV2ylB3x7LP2x3374rAAzuXkXH4Z1TmLr+02lM/ZgZQ4b8suoc7C7b0UVntDDAxiWJDrfHLmzCnvh9gB4+N/bIIdOnRIbv34z3/+Y9hCwg0YMMC88MILks6zjorx5aP5BfouLJcVMItQE0bc2XX77bfL7AIbZsCyHUM6MwB6UWYf2gtDm14XiygLF7wnBi3gtXyFCnKjSds72skFCMBpudUP5OtyeVb54euIw1bTG9NnmDlz5oi8GFV63X+/qVM3dstLZy6UU0eg5JRZ81c6+pyODc2YoXnLV1vMxIkTzbx33hG5Y1iyd58+pvL1VSTLqPNRYoxE+YCGhpPD08XE0dEeftkaXLRokRj20FmvJ48YO4nMYomrV6+et26RrLK6vU2o3gM4HQnxNcyhlBo1akgPVbBgQbtkyZKgZHif5oACesOXSTNmzPBgtcf3IpIQgG758uWFLieXZs2aJSNGQiQok1sujlTyBRRfrl1ZvIQdNnSY/XFv7Gii5U4JrwnxdDHTKTsnw+KbsaxdvUaOEfPtPrsUHC/l5Jk6cFPqVP7QCaR3cP8BO2L4czLTyhoWYZs3a2Y/WLTYO/POTomLHx+NlPJ3MfBpS/HJP6G8A+WVELybjgUPT3gqxGC+i6iZvvjii6JsTKlff/11D0QVROHU5zUAxUTxy5UrZ+k0cC4fHpFEBBDYfffdJ/TCwsLsnDlzPCxo4oBxy6TxyhMwhDGkgB10js5uWP+ZR4fjdOAoHYV38WOBL78Q5aB80b9YZeaDIfa6+WAoPCxcOtbXXnst3g9XklNq8nV/0GBbcdYb/2fr1LhRzhRUq1zFTpkwMc4xYuU1ME+3fgLT/snPKn98XKBM3PIGwianXEwX4mSiGQcjBgMKw3sg54xRYM43q/URhQlkUPGwFgIOP3e0J11/mr/i6LP6Gs/uA+sE0Orevbsmiw8MvOAUXgF45qcNReF+/fVXe+rkyWgwlP2vKHueX0CFxEdTaV9OvsrBLV/gRwG/HDpsR48aLXXNGfYmTZrI9U5c3ZQYF4e2IvCtkDNbIPzxxx/b1q1a2RwRWeUjpWFDnrIH9kVbilE0fGD5aTtTX+Nd2H9yWMsAj8HKQLybpuUBN7lOlD6xyCpUzXDRokWe8r700ksJkoF5HIqq5oK6desmcSqAwAJqnkpc4ZQHLImg8Izy+qmiwvp+6kpg27Zt8iEJH53wAUnXLl3tJucTXsktpi1qvXk+3xzQgGNO/J13epZvvv7GPtivvy3Ap8H58touXbpIG0ld7n1qKoEkKb0qrfpqzQOFW7FiRXSdh+iBVFH5qolVfZS1Tp063tRNGwiEVPmVUX3G1/w5D6AfI2DnjH15310YCajMoc6IjKmobFmzRq99PD1Udjs0Z/SeunTrTJ/PxXxdBuwvhw/bl0aPseXKlJUdkoa3NbDvvvOu9wUaMEpDaft+yiWQaGPbupLI6qaGDxw4IIudrNgnxti/rjRmy5bNM+n7008/maNHjwodpcsDK5gKr88C5Pxhu/znn3+WGE4vwQfOpeOA+8EUSACZsnqM4wQfZzvGjRtnihQuIrsw7e+4w0ydPMWwl87CO3Wn9SA+38WkT28yZspkMPv89qzZpk3rNmbIkCFyfmL0mDGyY9C2XVvZ0dGVarcNpIB9H9WRQKJNYCN8rUgO6bDdgMlmHHa/sR2OC1VJui3HIRlM/+K4KUTth7v4NAwOJoDDRQJ85aS01cdksJoJdk0JC2H/L1UloDLXOuT+9nu6dDENbmtgZsyYYaZNm2YGDRxo3l+40PS4v5dp3KSJyZQxunm5x0XXrFptxo8bJweosmXPbvr162d69uplrrr6qmh+rTF/RcUeRtH8UrUwaZxYopVee21XXm5D0FEAOI13YV18KpIfDqP/dAI4RgJGfs4bc0/Y//73PzmNVLRoUTnFh7139tY1D3ylCz2Njy9/ycD/S5EEVL4qc/bTCxUpbJ4Y8qRp0rSJmTxpspk3b57ZsHmTaXH77XK+Qa+L2rl9u5k+dZqc2Dx27Jhp1qyZeaBPH1Ozdq1Ynmz0LM3tJPy6jBVPqoWS+obgvmPxUT+zaU4ScRoO56YHo41hgAYNGggu1j31XXzr1q2WK3+hyUJfpUqVZFtP7//mbm/O8atju69KlSoC36xZM4ulFJyuDbi+4vh+yiSgMhU5Ozs5PLPTsXjRomiTXVnCbLnSZeyYkaPs+NfG2UoVKtqwLFlkDWfO22973z/8nZu4q9Lk57vUlQCjY6JdYAU899xzonBYE5k3b57QcRuFS9jtDDjvX6pUKcHFGKHSRek56PPEE0+IpVHwOYK5fPly7/ANJotYwMOxZaQLeaVLl/Y+6lEe3Dw1D5cnP5wyCaic8ZG1uuNHj9kZU6ba6tdXtbmyZbc5s2azdNgvv/yyV0fA+nWiEru4fpKUXpWIvW0cq7gYA2RkfuSRRxLkXBsGHQQn8sDDhhiONE6HBbMUu2DBArnpAzthaiscPCyQQgd6gR2PNka/cSVYNckGUNl6snYMW+zdvcc+NvhR269PX0uHrk7bkbYHjff9iyOBJCm9VrBWFkYY9QhuiRIl4ty0Esi+4rjbbNws8vXXX3ugCuNFxHQGPPNpbrFixUTBFy5c6IGsWbNG9uhRfK4AUvPAzBCgp43RQ/ADqSoBZKyDgLSP89aeO+tY2gmYnQMDfHx1naqM+cSCSiDRW3a6iKCrqSzmsGLeq1cvSeKGTT7+1wU6hVefRTrclClTzAcffCDhjh07eh8OQA8YFgShoQtziseCjoZ1pwCcWrVqmQ4dOgi9jz/+2Dz//PMS1sVB8PzFIBFJqv9pnUGYMO68PW/SZ3CaVcyHM6QrDAt11KU+pzpjPsHQEgjaHcSToKMmvvTqMdY6uX+Leuf3wAMPxHlvUzKMvBMmTPA+H+Qwzf4YG23a+7t0GQl0pIbGRx99JJ/FchpsX8Anlbt27fLe+XndYIGR02PB3IkTJ+ypU7EmooLB+fGhJRA4Wrv1p+0DChpWPzRVP/VCSyDRn9aG6jqw+tmjRw8xngEc5opatmwpFjwZcflc88MPP5S9WdK5d50RH5/ePnAkdkcFHamZFbz99tumd+/e5vXXX/fwFB/rpX369BFDEOTBYZ2bb75ZjA1gjRQjBZwr2LFjh8BgHorPgX3nSyDNSSClvYr29rxLs+qut2vqyO/6LMJxQ0dSbviEv9mzZ1u+4uPTXTUhxMyBkYP3Q8I4dgUGDRpksXPu5htfmJ0H3/kSSIsSSPFIr+/w+r69c+dOeWdn5OWYLqZ+ChQoICMuxzerVIk2fqCjueK5va2bhtmtFi1aiCEOTn1169ZNQHn3591QDwURqYc6du/ebVauXCkGOzimi9kuTpDlypVL7IZjfxzTXQULFnSz9cO+BNKEBFKk9KqcKqlABWZKjeOyAHXgoKi6kKOKqun4wDCt//bbbw0WeLB2g3XQZ599Vhb4dMqv+evrAc+BPEAPPlweNC86rPjgNd33fQn8GyWQIqVHIK7ioXyqsPEJCyVzYVRZ3XhVQm4K4T1+w4YNcj77lVdekZFcZxbQV3w3L40Lxofm5fLh4vthXwL/dgmkWOlTKiCUk5EfJeSH0nOtEArP2XvO27/88ssmS5YscUZ5V3lTyoOP70sgLUnA2VC9dMVG0VXhv/jiC9l3Z0qPSeDx48eLwsOdwimndBi+8yXgSyBpEkj0V3ZJI5s4aJRWp+EoPQqPRdvvvvvO1KhRQ+zTv//++/L9tb77szDIRYI1a9aMd3qfuJx9KF8CaVcCl3R6j8IzTdcRvHnz5mbx4sUJ1karVq28MwEJAvsAvgR8CcSRwCUd6fU9HsVnJK9fv77hCmDe38+dO+cx6k7jWYnn6K3vfAn4EkieBC7pSJ88lmO39JKL7+P5EkjLEvhHLOQltQKYIfjOl4AvgeRJ4LJU+uQV1cfyJeBLAAn4Su+3A18CaUwCvtKnsQr3i+tLwFd6vw34EkhjEvCVPo1VuF9cXwK+0vttwJdAGpOAr/RprML94voS8JXebwO+BNKYBHylT2MV7hfXl4Cv9H4b8CWQxiTgK30aq3C/uL4EfKX324AvgTQmAV/p01iF+8X1JXDRld79Nj4h8ScFNiFafrovAV8C0RLIqAYmeVRjFoHCUZiEPmlFSROCUXPUweCUBsYylR8XVtM1jmd+6rDCozBuGvE4Nb+t+MQFK5/CKh+ah+an+UBL44AhrDhuPpqm6XrfHrC4+GA13qWvZRGkeCwSu+VR2oE4iuv7aU8C6WLuF/Psv3MJJD9cmTJlTKdOnbxLJLZs2WKmTp1q/vzzT7l04rrrrjMjRowwR44cMc2aNZOrrEaOHGm4zLJevXqmTp06YsmWxvz777+bzp07Gy684BosLNz+9ttvooQ5c+Y0N9xwgzl58qS59957JW9s4alSJKVaUI5A5QnER5mx1PP999+bTz/9VAxxZsqUSa7NKleunOGyDKzzFCpUyEM9fvy4GOl88MEHTVhYmBcfLEAeZ86ckXL+9NNPIt/MmTPL1VulSpUSNK7puvLKK8XeH8qZWMVcvny52A/kYpHw8HCRXTA+iIcXZJJY+qFo+WmXvwQyPP3008NUCdatW2cmTJhgUEIUm9tlDh06JLfT0GCwX4dRSn4o/4kTJ0Thb731VjN//nyRxqpVq0S5p0+fLorDTTI0dgxc3n333XLbDcpMY+eOO26gGThwoDl69KgZN26cNMxTp05J+q5du8x7770nnQF5rl+/Xn50MseOHTOffPKJ8AKvCxYsMCgXCkXnMW/ePKF/1VVXmT179pjPPvtMypM3b165bRdmMbUN/bZt24pSYHk3f/78cjHG1VdfbTZt2iQ35cAPncSQIUPMH3/8IfRJp/MCn06O+/LoRJYtWybKXrRoUSkTt+gOGDDANGnSRO724449yoUskSEdCwqJzH/88Ue5jYcw8tq3b5+Uh5uCeMbnlp6ePXtK3uRJeeggKS/8IFfKtWbNGrkkhPyQN/WXUGd4+TdnvwSJkYDYyNMRgBGeRoPSVK1a1WCokmulaYzE6yiM1VouoaCRYbUWpWH04QcencCMGTPkwsjbbrvNTJo0Sa60Ll++vPBEJ8AsAsXBlS1bVhSE0RTT13PmzDEPP/ywmT17tig1Co2iv/TSS4aRGH7w6TSI55WBzoarq7JlyyYXZaIgKCsw8ImioYhr1641XJwBD8BieRfb+jjs7DNjQZFROMqDYtEZMTNB8emkxo4dK4qGDJgVwDf5MBMiPHjwYKHHrTrY+3vjjTckLzqkBg0amGHDhpmSJUsKX8wGXnzxRTNmzBizZMkSoU/a3LlzPUVlNgJdOuHu3bsLTXjh6i7KTGfD1WHIiUtCIiMj5courvOiQ0KWvvMloBJIrwpPBGF+THVRJpSLxuWOEAcPHjTvvvuuGTRokOGeeEYZptRMeZkx6DskDZ4RBuWj4bVu3VrzFDgewOWHQ0HpCFAAbrNdunSp8MGd94ySdD40bG6mrVu3rkxpacw0eJQJXuAVvpmx8JrBD0Xm1YJZho7UdBI4jG8yE+DGXRS/dOnSwj+8M1Jy8y7Kjrnt06dPyyxg6NChkj8KCAwzg2uuuUaUDzlBi9capQ+tLl26yG27bdq0MZs3bxZ58VrUuHFjmVGhuMiPH/JD+XmNwOe1R19zmNGg/NwHyP1+uXPnNkzxUW7uCLjnnnvM6tWrBZ7ZE/ky+/GdLwFXAundd2CudmYqjPIw3f7888+lYTFC4hhJ+vfvL9N2Rkks13JRJVNnpr3gb926VUY8RjCUCMUoUqSITEvJi0atnQhKh7LjiEex6ASgxeWSKCtTbGYWTFOhCbx2NMBBg84GS7ooBaNcvnz55GrsRYsWyQhLJ4aig6vvt+QJPGWlk6lYsaJM64GBD3imbLxS7N+/X3gGHh6YCdE5whP50gnBL7ThyXXQY1ZBp0T5kSWKi8yYKfBODh5y4nUFXnmVYUYyefJkmXXQ4dEh0unxSgVN7vmjjqgHygAtcJQPygsv5Ok7XwKuBDIMHTp0mCo+jZhRhykrisUI2q9fP2mIIKFEjNyMLEyXmzZtKqMqisG0lWk+I+CKFStkmk8ctFBClAqnMwsUn/fy7Nmzm8qVK4ui0fhZA+AeeToQ3nfffPNNUQJGYvLl9YGRD6Wk00GZGGmZGZBPr169ZBFx1qxZhlkJ99CjWCgSOCgsIyXKhRJTzgoVKghvLCzyygGPLGAy0+Hd252pVKtWTZSORUwW+5i6k05ZocmrinaSECWNVw+m4ozCDRs2lHLxCpMnTx6RGbzxzo7yNmrUyGDXn1Ee/rnAkzqhM2VWAe9M/+kI6VRr165teG3idQpZMhOiYwIOOVF2fa2SQvp/aV4CsnrPKOsqY6BU6BT4KUxgerBn7UxIJ6wOhXfT3PzdsMKnlk+ngmIpLzrjIE+cWz5eG7gam4VMOh9eDZh+u3wH40vp47s0g8Ff6HjKTVn/Cbxc6LL69BOWQLqoqChLg6Bh0Cj4aaNV5dRnyCksvj5rYwpUHkZRfR+FhtJRupoX8cS5Cu/SCsTTvBXPfdYik+bSV9r4wCvPwCkdLQ8+U2hGWmCZATFFVxqBODy7uO4zYfC0s4Ge4mscciLs0iAMnJYBPOjgNE7hlR4wSl/TFEfThID/l6YlkO7cuXMWxdTGgTQIq1KodGg0dAw40nhWHBosYY3Txgysjq7qA6ONXONotDhowAvPCqN88Kz5CrDzp3yQrnwov+TBYhpO81EetENSfOI1P4e8hwstYKADDtN55Sswb5CAAUfzAaMKJ3QAAAArSURBVE95UCVXmooPHmHlEd+VL+mav/ILDeWbOBxxwKk8NV0S/b80LYH/B3L8G4RUphVaAAAAAElFTkSuQmCC />
1.NAD+ and NADH
2.FAD and NADH
3.H+ and CO2
4.FAD and FADH2
5.None of these"
Question 3Which of the following is not a name for the same pathway?
1.Krebs cycle
2.Embden-Meyerhoff pathway
3.TCA cycle
4.citric acid cycle
5.Tricarboxylic acid cycle