|
|
|
There are more bacteria in your mouth than there are people in the world.
About one in five American adults and teenagers have had a genital herpes infection—and most of them don't know it. People with genital herpes have at least twice the risk of becoming infected with HIV if exposed to it than those people who do not have genital herpes.
There are actually 60 minerals, 16 vitamins, 12 essential amino acids, and three essential fatty acids that your body needs every day.
Adult head lice are gray, about ? inch long, and often have a tiny dot on their backs. A female can lay between 50 and 150 eggs within the several weeks that she is alive. They feed on human blood.
HIV testing reach is still limited. An estimated 40% of people with HIV (more than 14 million) remain undiagnosed and do not know their infection status.
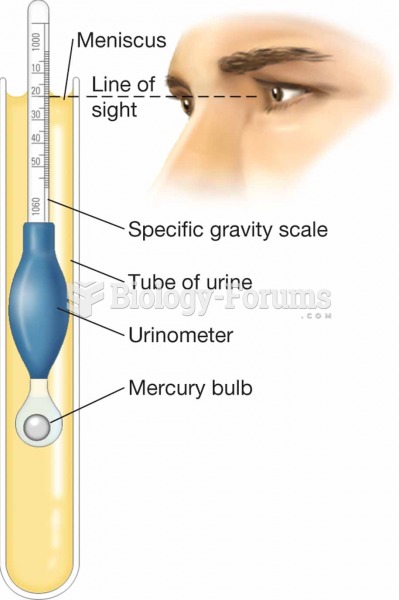 Urinometer. In this procedure, a urine sample and urinometer are placed within a tube, and the liqui
Urinometer. In this procedure, a urine sample and urinometer are placed within a tube, and the liqui
 Increasing access to care for teen mothers is important because they have a higher rate of pregnancy ...
Increasing access to care for teen mothers is important because they have a higher rate of pregnancy ...