This topic contains a solution. Click here to go to the answer
« previous next »

Author Question: Consider the unit cube Q = in R3 with the standard orientation given by .Express the orientations of ... (Read 79 times)

karlynnae

  • Hero Member
  • *****
  • Posts: 599
on: May 27, 2021

Question 1

Let M be the smooth 2-manifold R3,  x = p(θ, φ) = (cos(θ)sin(φ), sin(θ)sin(φ), cos(φ), 0 ≤  θ ≤  2π, and let  be a parametrization for M. If M is oriented by the differential 2-form ω = zdx∧dy, determine whether the parametrization p is orientation preserving or orientation reversing for M.

Question 2

Consider the unit cube Q = in R3 with the standard orientation given by .Express the orientations of the bottom and the front faces of Q as differential 1-forms evaluated at the cross product of vectors u, v in R3.
Calculus: A Complete Course ¦ Adams, Essex ¦ 8th Edition
Buy Test-Bank


Related Topics

Need homework help now?

Ask unlimited questions for free

Ask a Question
Marked as best answer by karlynnae on May 27, 2021

mcni194

  • Sr. Member
  • ****
  • Posts: 311
Reply #1 on: May 27, 2021
Lorsum iprem. Lorsus sur ipci. Lorsem sur iprem. Lorsum sur ipdi, lorsem sur ipci. Lorsum sur iprium, valum sur ipci et, vala sur ipci. Lorsem sur ipci, lorsa sur iprem. Valus sur ipdi. Lorsus sur iprium nunc, valem sur iprium. Valem sur ipdi. Lorsa sur iprium. Lorsum sur iprium. Valem sur ipdi. Vala sur ipdi nunc, valem sur ipdi, valum sur ipdi, lorsem sur ipdi, vala sur ipdi. Valem sur iprem nunc, lorsa sur iprium. Valum sur ipdi et, lorsus sur ipci. Valem sur iprem. Valem sur ipci. Lorsa sur iprium. Lorsem sur ipci, valus sur iprem. Lorsem sur iprem nunc, valus sur iprium.
Answer Preview
Only 35% of students answer this correctly


karlynnae

  • Member
  • Posts: 599
Reply 2 on: May 27, 2021
:D TYSM

triiciiaa

  • Member
  • Posts: 349
Reply 3 on: Yesterday
YES! Correct, THANKS for helping me on my review

« previous next »
 

Did you know?

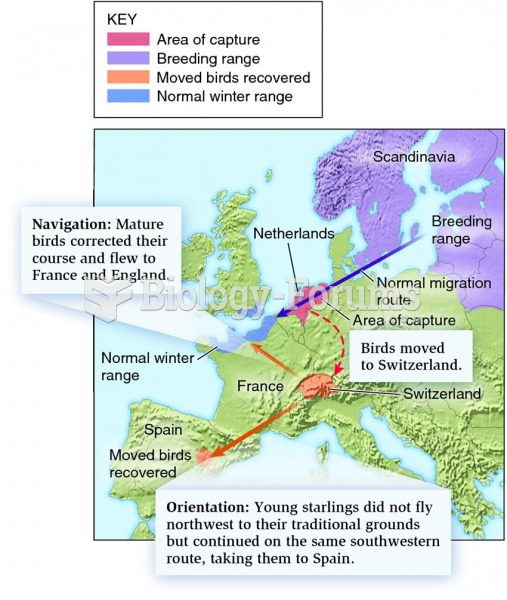
Although puberty usually occurs in the early teenage years, the world's youngest parents were two Chinese children who had their first baby when they were 8 and 9 years of age.

Did you know?

A serious new warning has been established for pregnant women against taking ACE inhibitors during pregnancy. In the study, the risk of major birth defects in children whose mothers took ACE inhibitors during the first trimester was nearly three times higher than in children whose mothers didn't take ACE inhibitors. Physicians can prescribe alternative medications for pregnant women who have symptoms of high blood pressure.

Did you know?

Many supplement containers do not even contain what their labels say. There are many documented reports of products containing much less, or more, that what is listed on their labels. They may also contain undisclosed prescription drugs and even contaminants.

Did you know?

The U.S. Pharmacopeia Medication Errors Reporting Program states that approximately 50% of all medication errors involve insulin.

Did you know?

Amoebae are the simplest type of protozoans, and are characterized by a feeding and dividing trophozoite stage that moves by temporary extensions called pseudopodia or false feet.

Orientation versus navigation. Orientation versus navigation.
Mixing schematic Diagram CHE 415 unit operations experiment apparatus Mixing schematic Diagram CHE 415 unit operations experiment apparatus
This unit is applying smoke to the fuel tank through an adapter and the leak was easily found to be ... This unit is applying smoke to the fuel tank through an adapter and the leak was easily found to be ...
Cumulative Standard Normal Distribution Cumulative Standard Normal Distribution
Standard Precautions for the Care of all Patients in All Health Care Settings Standard Precautions for the Care of all Patients in All Health Care Settings
Which of the following is not a unit factor related to a 15.0% aqueous solution Which of the following is not a unit factor related to a 15.0% aqueous solution
Video: Embryonic development - week 1 and 2

For a complete list of videos, visit our video library