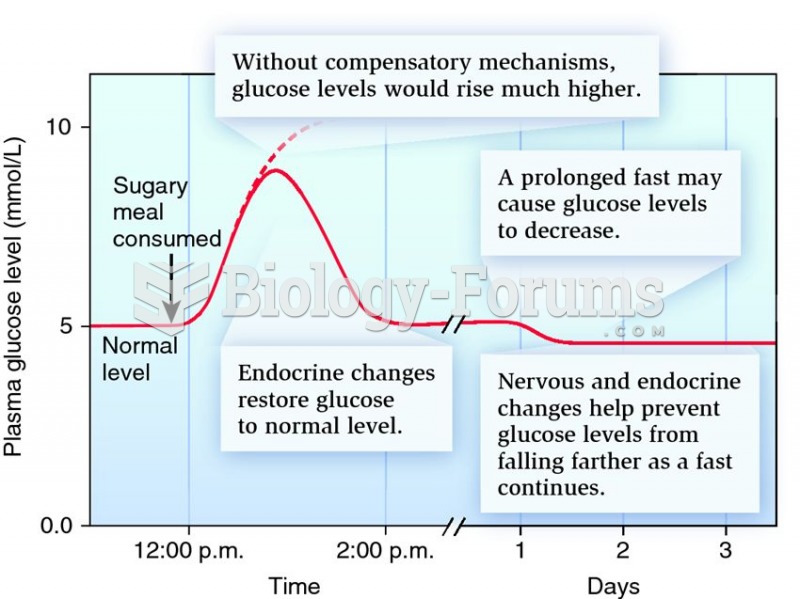
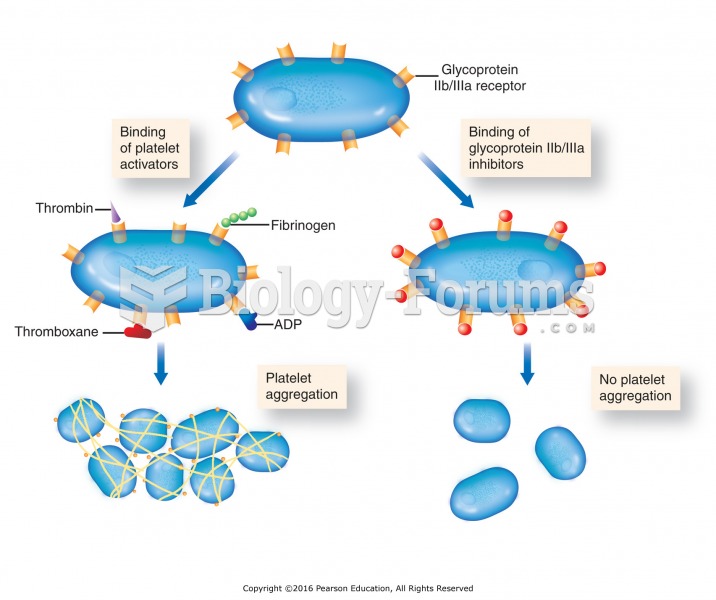
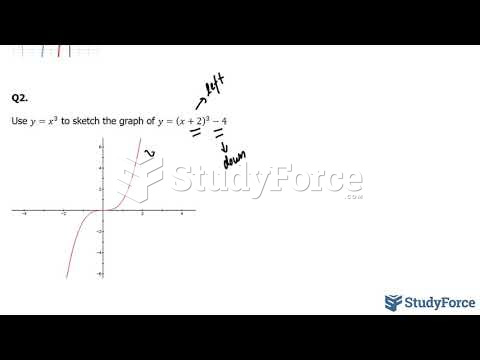
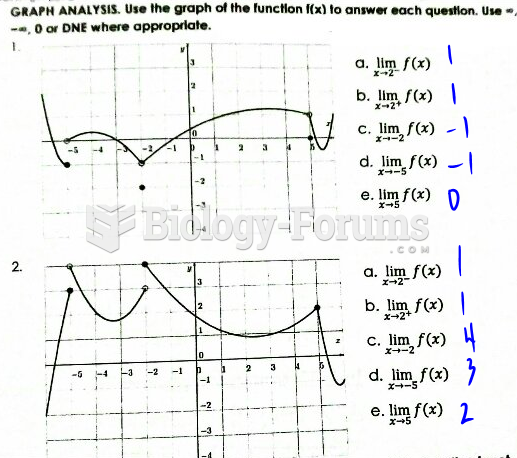
This topic contains a solution. Click here to go to the answer
|
|
|
Did you know?
Cyanide works by making the human body unable to use oxygen.
Did you know?
Warfarin was developed as a consequence of the study of a strange bleeding disorder that suddenly occurred in cattle on the northern prairies of the United States in the early 1900s.
Did you know?
Limit intake of red meat and dairy products made with whole milk. Choose skim milk, low-fat or fat-free dairy products. Limit fried food. Use healthy oils when cooking.
Did you know?
In ancient Rome, many of the richer people in the population had lead-induced gout. The reason for this is unclear. Lead poisoning has also been linked to madness.
Did you know?
Asthma is the most common chronic childhood disease in the world. Most children who develop asthma have symptoms before they are 5 years old.