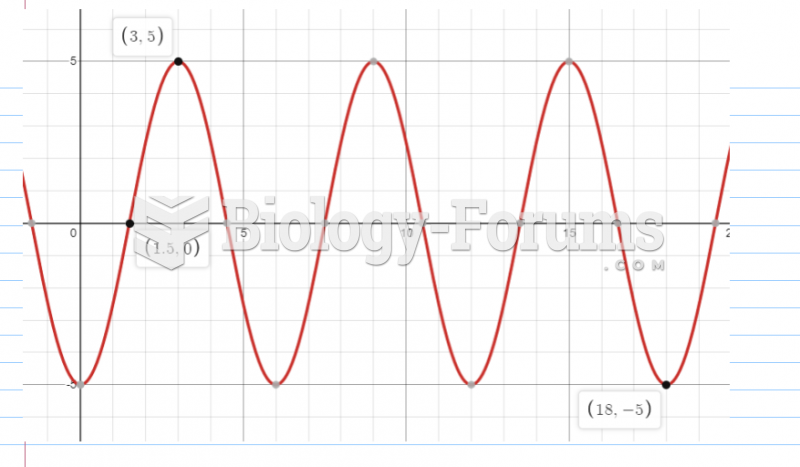
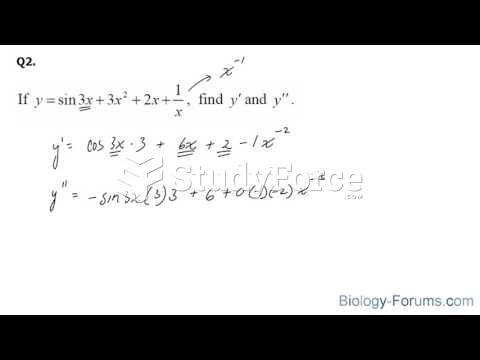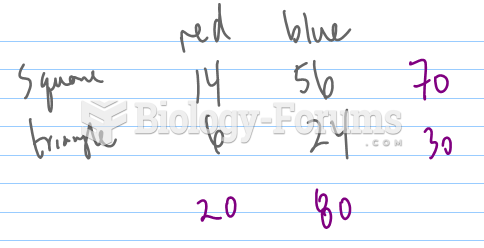|
|
|
Carbamazepine can interfere with the results of home pregnancy tests. If you are taking carbamazepine, do not try to test for pregnancy at home.
Only one in 10 cancer deaths is caused by the primary tumor. The vast majority of cancer mortality is caused by cells breaking away from the main tumor and metastasizing to other parts of the body, such as the brain, bones, or liver.
To combat osteoporosis, changes in lifestyle and diet are recommended. At-risk patients should include 1,200 to 1,500 mg of calcium daily either via dietary means or with supplements.
Walt Disney helped combat malaria by making an animated film in 1943 called The Winged Scourge. This short film starred the seven dwarfs and taught children that mosquitos transmit malaria, which is a very bad disease. It advocated the killing of mosquitos to stop the disease.
Medications that are definitely not safe to take when breastfeeding include radioactive drugs, antimetabolites, some cancer (chemotherapy) agents, bromocriptine, ergotamine, methotrexate, and cyclosporine.