« previous next »

Author Question: In a continuous probability distribution, the probability that x will take on an exact value: a. is ... (Read 66 times)

cartlidgeashley

  • Hero Member
  • *****
  • Posts: 572
on: Jun 24, 2018
In a continuous probability distribution, the probability that x will take on an exact value:
 a. is equal to the height of the curve at that value.
  b. is calculated using the probability density.
  c. is always equal to 0.
  d. is always greater than 0.
  e. None of these is correct.

Question 2

Which of the following are not correct concerning the probability distribution for any continuous random variable?
 a. The vertical coordinate is the probability density function.
  b. The range of the random variable is found on the y-axis.
  c. The total area represented under the curve will be equal to 1.00.
  d. The probability that x will take on a value between a and b will be the area under the curve between points a and b.
  e. The area under the curve represents the sum of probabilities for all possible outcomes.


ErinKing

  • Sr. Member
  • ****
  • Posts: 362
Reply #1 on: Jun 24, 2018
Answer to Question 1

C

Answer to Question 2

B


Related Topics

Need homework help now?

Ask unlimited questions for free

Ask a Question
« previous next »
 

Did you know?

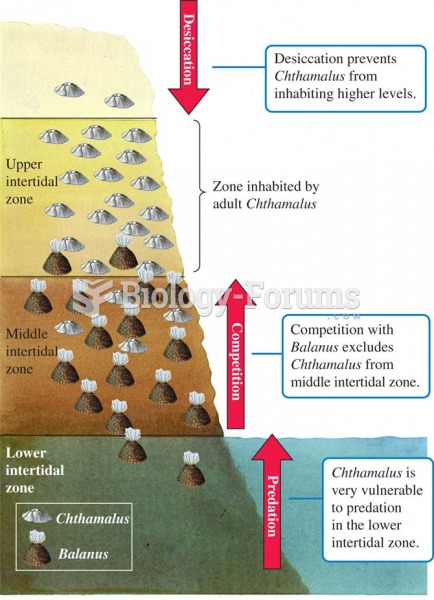
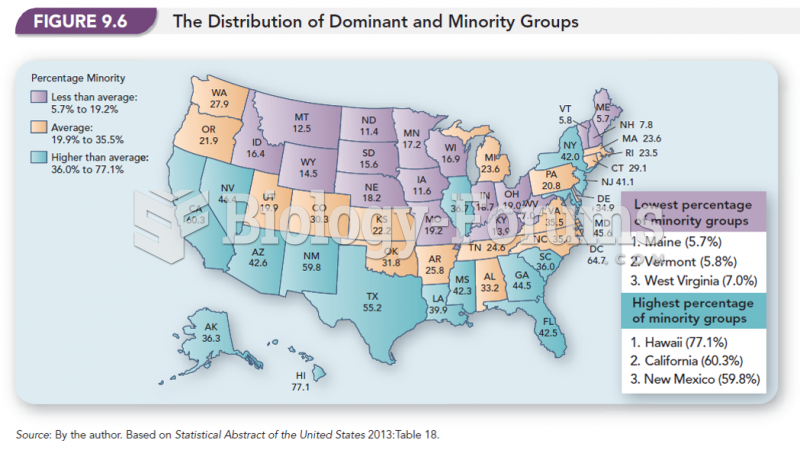
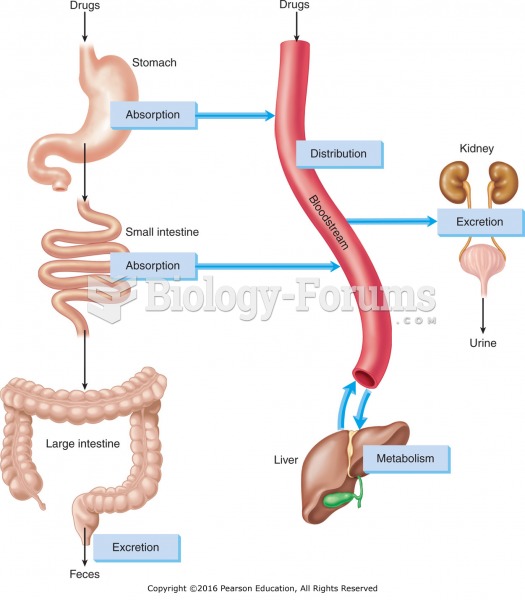
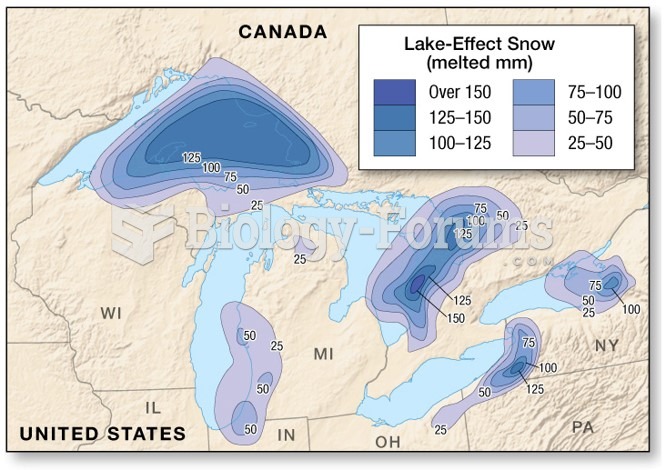
Oxytocin is recommended only for pregnancies that have a medical reason for inducing labor (such as eclampsia) and is not recommended for elective procedures or for making the birthing process more convenient.

Did you know?

In ancient Rome, many of the richer people in the population had lead-induced gout. The reason for this is unclear. Lead poisoning has also been linked to madness.

Did you know?

There can actually be a 25-hour time difference between certain locations in the world. The International Date Line passes between the islands of Samoa and American Samoa. It is not a straight line, but "zig-zags" around various island chains. Therefore, Samoa and nearby islands have one date, while American Samoa and nearby islands are one day behind. Daylight saving time is used in some islands, but not in others—further shifting the hours out of sync with natural time.

Did you know?

The ratio of hydrogen atoms to oxygen in water (H2O) is 2:1.

Did you know?

Many people have small pouches in their colons that bulge outward through weak spots. Each pouch is called a diverticulum. About 10% of Americans older than age 40 years have diverticulosis, which, when the pouches become infected or inflamed, is called diverticulitis. The main cause of diverticular disease is a low-fiber diet.

Environmental factors restricting the distribution of Chthamalus to the upper intertidal zone. Environmental factors restricting the distribution of Chthamalus to the upper intertidal zone.
The Distribution of Dominant and Minority Groups The Distribution of Dominant and Minority Groups
The four processes of pharmacokinetics: absorption, distribution, metabolism, and excretion. The four processes of pharmacokinetics: absorption, distribution, metabolism, and excretion.
Distribution and Forms of Precipitation: Snow Distribution and Forms of Precipitation: Snow
World Distribution of Temperature World Distribution of Temperature
Distribution of H2A.Z-containing nucleosomes near a transcription start site (TSS) Distribution of H2A.Z-containing nucleosomes near a transcription start site (TSS)
Video: Properties of water -structure of water and polarity (Ionized and polar compounds)

For a complete list of videos, visit our video library