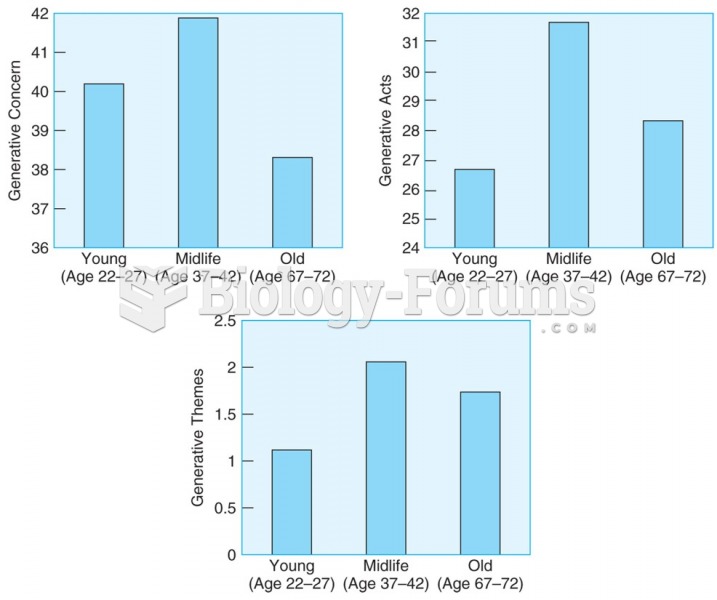
|
|
|
The average human gut is home to perhaps 500 to 1,000 different species of bacteria.
Side effects from substance abuse include nausea, dehydration, reduced productivitiy, and dependence. Though these effects usually worsen over time, the constant need for the substance often overcomes rational thinking.
In inpatient settings, adverse drug events account for an estimated one in three of all hospital adverse events. They affect approximately 2 million hospital stays every year, and prolong hospital stays by between one and five days.
To maintain good kidney function, you should drink at least 3 quarts of water daily. Water dilutes urine and helps prevent concentrations of salts and minerals that can lead to kidney stone formation. Chronic dehydration is a major contributor to the development of kidney stones.
Serum cholesterol testing in adults is recommended every 1 to 5 years. People with diabetes and a family history of high cholesterol should be tested even more frequently.
 The 2012 U.S. presidential campaign rang with “get tough” cries to end Iran’s nuclear capacity and c
The 2012 U.S. presidential campaign rang with “get tough” cries to end Iran’s nuclear capacity and c
 A passenger train crosses Stony Creek Bridge in the Rocky Mountains in 1878. Railroads were importan
A passenger train crosses Stony Creek Bridge in the Rocky Mountains in 1878. Railroads were importan
 Midway Island, an inhospitable atoll acquired in 1867, was valuable as a military base located midwa
Midway Island, an inhospitable atoll acquired in 1867, was valuable as a military base located midwa