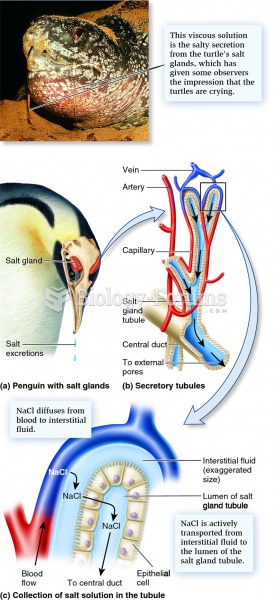
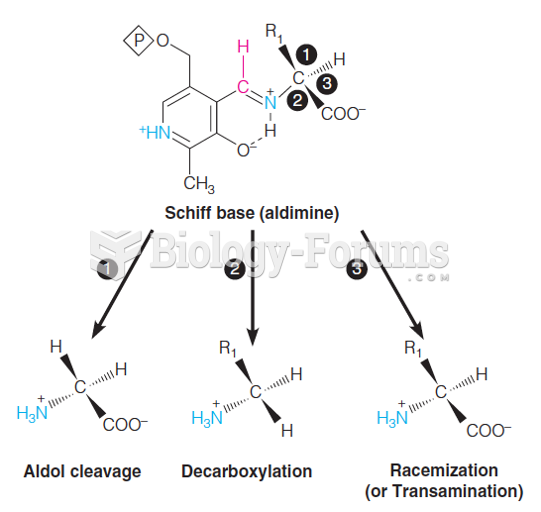
Most Wittig reagents must be generated in situ from a phosphonium salt and base. The phosphorane used in this experiment is one of the few Wittig reagents, known as stabilized ylides, that can be stored in a bottle. Explain what makes this particular phosphorane stable relative to, for example, Ph3P=CH2.
Question 2
Devise a synthesis of the product you obtained from this experiment starting with 3,3,3-triphenylpropanal.
Question 3
TboJ//8L94x5YPKnDlzljHE1ksvM13tzepv9lAemVGmG/aUVv8JSmNcLAOIMmMrx8nmzZs9bYxDgG31EvSPElACSkAJNHkC3AQhXkMmTZxkNgE6VssAcndZ4z2joe4XagDF65na6boLXG0mGqMEmiyBigFmjvHuXUndBts2Rrr36C4ffnhQsMEAvkOEIf0+xviKZwAtX75c7r4rvEMcYfOG0Lt3HzM1LfzRNsbZZfbq3Us+MOtx2pqd3I6a3ebgeBOhPOOqJleZedZbPRnGwV+4aKE8+ui6WvHMH80A6tmr3BiYe7x8pSXYcvyAd8x8CLAuXoL+UQJKQAkogSZPgAYQZl40b948oj34gOikiRNl3aOPyqhRI+XJJ2s2wOG9IZoBlK6jKxGAUjSgBlCKdoxWSwnUh0D/iv6+AfSytZ30zbfcbBbw75Lnn3/OU1ufh3ReyG1jBAYQtpWmGzVydMTCTuZheSNGjjBT8nZ4u+XMmT1X/vSnP8mqlSvl8Sc2yMmTJ7xvGJw9E17PBJ3Mb5dJA4hllpuPvr618y0vSHkEUCYMoL+YLbCxQQJcB/MF7AH9+5tpcS+Y9HNSVFzsrSli/ez8XoYYf9QAigFHk5SAElACaUSAIyyxDKB7fxe5sQ+az3sK7zFEwng1gEik8X01gBqfuZaoBJJGINoIULIMIDSEF/IB5gOl27e/EtE2ptkX/+KSYikvL5dt28IfIWWGPmbk5x2zRXU8AyhWmSwPMnaZ2TlZMmH8RDNlbZOcv3DemxqI7/XQUdbOzzT6bc16qwlmesMLxoj8+JOPI/Tb+aiL+dRXAkpACSiBpk2ABhBaUZdrPO8Nbh7GqwF0+c4LNYAuH3stWQk0OIGmYACh0WMqx8jwYcPlgPk4aft2pfKrO34lMIBer576RjC8SdgjQEhjvGt0MR4y7g1n9uzZDWIAPfjAA1Af4WKVGyGoASWgBJSAEmhyBNQAanJdFrfCagDFRaQCSkAJpCMBNVrSsVe1TUpACSiBhiegBlDDM73cGtUAutw9oOUrASWQNAJz586VDU887uvnqFDXbl3l4MHwBgZTp0yT9evX+zJ6oASUgBJQAkrAJqAGkE0jPY7VAEqPftRWKAElEEAABtCTTz4hX4a+DEgV6datu7y9++3ANI1UAkpACSgBJQACagCl33mgBlD69am2SAkoAYdAec8esnfvXrl6yVI5cuRTz/C5+567pKPZFU4NIAeWBpWAElACSiCCgBpAETjSIqAGUFp0ozZCCSiBRAisNFtu0wC6/fbbE8miMkpACSgBJaAElECaEVADKM06VJujBJSAElACSkAJKAEloASUQHQCagBFZ6MpSkAJKAEloASUgBJQAkpACaQZATWA0qxDtTlKQAkoASWgBJSAElACSkAJRCegBlB0NpqiBJSAQ+DH//AjL+affvLPTkpNkDKIiSVXkyPyqLKyUt588w05fea0l9ChXQcZP3Gi3H3XXZGCAaFu3bvJgQP7I1LGj5sg48ePlX/8x59ExKdLYN68uV5THnlkXbo0SduhBJSAElACSiCpBNQASipeVa4EkkugX/9+8s47wds4Z2Vly7GjxxqsAu3bt5dPj3zi6eP3dIKU8wOjXbt2k3fefidIJDBuzJjRsu3lbYFpiGzWrJmc++J8YHpeXq5vMAUKVEfOmD5d1q17LJZIk0sj71h90uQapRVWAkpACSgBJZBEAmoAJRGuqlYCySZQUloiR49+FlhMUzOAMrMz5fy5c9KyZSvp07uPvP7Ga167Bg8eYraq3u0ZODk5Od7W1a+/9rrf5jZZbeTC+bBhNGL4SNmzd4/MnDlTsjIzjbGzTq5Zs0Z+aXZ8O3rsqJcn3QwFNYD8U0EPlIASUAJKQAkkREANoIQwqZASSE0CePjNyMiQs2fP1qpgUzKAhg8fLq++tkPamelu2Kb69Ofh6W9sVHFxkRw7XjOaZRsxNAAgCwPo+eefZzbPx5S8X/zil/L5mVNy4cIFmT5tujz6aPqMArH9NpMIABpQAkpACSgBJaAEIgioARSBQwNKoGkRwMNvn9595fXXa0ZEktWCZE6By83LkTNnzsjkqsmyYcMTgU3gg/6YMZWy5ZktnsyQoUPkjTfCbZ85c5Y88vAjgXkRyfwYYXINrKiZmkAC26UGUBPoLK2iElACSkAJpAQBNYBSohu0Ekqg7gTq+2XqupcUzpFMA6htfr6cOn1KWrVqLZ+f+jywiiNHjpTPzHS/TmWdZNOmTZ4MR45mmSlvIWkW0wAqKCyQkydPCNqxb2/kRgmBBcaJnDVrljy18clAqWnTpsljj67302ikNG/RQi6aUajcvDzp0qWrbN/2si/jHowdN1ZefPGvEgqZlpn1T/SbmXaeO1ezFoq6bQMo2pqojNYZhsEpryjm69atu5liWHsdWafOneTw4UPGcDQG46nIETm3rhpWAkpACSgBJdCUCKgB1JR6S+uqBCwCffv1k3ffDT+4zp49R1599VXJNOteRgwfIb/97W8tyYY5TKYBNHHSRDN17TmvoldddZVMnFQlTzy+IW7FW7VqaQyfkCdnGwDRMrbOaCVffvmlWWt0IZpIQvELFiyQx9Y/6sn27NlbsrOyzBqlM8a4OCkffnjAi1+5cpXc+ds7vWMYG8XFJfLJJx/LuLHj5a1db0mHjh2jGkCzZs00xtVTXt4BFQPlvFnjBN3l5eXyzJbNkpudJ0c+O+LrxgHbNKZyjGzb9pIxsLrIxIlV8sILL0hJcbGcMMbf66+/5o+yDRgwUHbt3unpYF4vYP6sXXut3Pu7e73gNDNl8LE0mjLINqqvBJSAElACVy4BNYCu3L7XljdxAnyDH60ZAwcOkpdjjDBEyxctvrCoUE6cOB4tuVZ8aWmpHNh/sFZ8tIiBgwbKW2+FH8htmcw2mTJ16nT5wx8etKO9YzLo2bOX7Hyzdl43Q0VFf9n99m7fWHDTEw2PGj1Ktm9/Wa66qrn06FFuyn7Ty9qla1c5dOigN1rTt08/ee218EYOrCdGb8aOHeePYEUrb6iZ2ve6mdrXrNlVUtG/wpS13ROdPWe2PPlkeIrgwgWL5IEHHvCn9tGIYVnIcO2118mv77jDy7t61Sq5/8H7pXnz5nL2zBde3PgJ4+Uvf3nBO2Z+BKhj6dVL5d57f+el6x8loASUgBJQAulCQA2gdOlJbccVR2DmzBmy8emN0r17Dynr0FG2PLtFCtoWyMgRI+TxJ8KjJ/ZD7aUCogFUNWmy5JkpXNHcZ599Jlu2PiP1MYDOnjkrH+x5XyaMD48Inb9wPmL6F6aQnT1ds+EDH9SnT5thNjYIj8hEqxfie/fpLe+//94lG0AsN2jN0miznffL1dt5kz/lGY5VR6RRfpxnLG2OEOe0P24zTlnqvvXWWz15GGf/63/d5uft2aun7NnzgQk3M+0PT6HLys4y0+m+kF69esubb4SNOGTobEaPYMh17txZ3nv3fV+HHigBJaAElIASSAcCagClQy9qG65IAnPmzpHjx45Ln7595Y5f/cpnsGzZctmy5RkzRepTL44Pxr5APQ/sKXAYfYjm/vTnh7wkPqDbcrPnzJHnnnvO7Fp32lsDE7T2BPJTpkzxpsTNnTtP1j++XrLMFLPPqqd8lZSUyMEDH3pq+fCfn9fWTC8Lf6PILs89jjUF7kd//0P51//5P7wssZhhi+2NTz8lWW2yzM50wSNirBf1uGG3XnZ41myztuip8Noi5rfT3eNouqdOnSovvvRXb3OJyDw1BtBc8xHVDRse95JZ1vXXr5W777nHi1MDKJKchpSAElACSiA9CKgBlB79qK1QAhEE+FCMSD7YRgjUI2AbQLF0smzbAFq8eLE8su5haZPRRqZPn+FtRvD0pqelwqxveaV6elesKpW2K5U+ZvSGW1yzfBhDR4+Fv4PEuFh6ULcu5gOt7wZ8oLXIbLV9vHqr7Vi6uPYq2uYBKJ8MMO3sN7+50w/H0st69zLt/MCMUrVp00ZOHD/J6Kg+y6LuUvNtKGwWQdffTKGrHDPGbC5xSu79Paaz1RhAkFlzzWq57777PHHooD5EUKeXqH+UgBJQAkpACaQJATWA0qQjtRlKwCZgL2JvqIfYSzGApkyd4o1K5efmmw0OJvkGEOrcz2zmcP78BXnnnbelg5nKt3fPXrsp/rH9YD5l8hR53GySYMfFaydl7TUwVN7SbKbQo0cPuXjxgpkmtifmg/8NN1wvd919l5c1Wpksi+lumOUG+dddd63cc294AwLmD5JjnKubYXxT6fDhD4UG0IGDB2X9+sdMtkgDqFfvXvLBB+97/fDqjteka7eucvDgAbNZA9YqbWYx6isBJaAElIASSBsCagClTVdqQ64kAkuvvlr+9PCfvCaXlrYzmw2Edx5DxJAh5ts4b4a/jZPo5gCJsLsUAygzO1O6mW2f37Q2KuCDOkZSjpp1Q/zQabTv+WS0aW0MlIvemqClVy+Te8w0rbKyMsnNz5N3zMYG7oO93SaWhbjWZivoU9VbQSM820w5e/75F+TWW/9G/uW//TdExTWADhpjAiNYQbIjRo6QHTte8ep57ovwWhuWn4hBAwPo5IlT8rAZMXP1T5s2VTY/s9mLxy5u21/e7huB1M2yYADt37fPk8Ufrn9yOcEAws57x44dlR7dzYYOb70pgwcN9vKpAeTj0wMloASUgBJIIwJqAKVRZ2pTriwC3bp3kwMHwt+zwRbLC+bPN2tTnvYWuuObMfb3W26+5WbZtWuXv9U0H5brQuxSDCC3HGx7jW/cFBcWe2uYXnllu1QMGCDPPrvVE83MzPLWAeG7NVu3bpHDHx324yv6DzDriJ71VRYUFEiLls3l6NGjXlxr8y2hocOGCabHYRc2LPwHD7gxo81HVLeEP6KKcNvCtsYYOim33HSLFBYVJGQAId/qVSvNjmoPGL3iGWFzzdqmD8zI1Vaz+QM+6JqZkSnTpk+XBx8M71xHoyRR7plZmWZU7ByKkvy8fFm2bIXs3r1bnnv+WblgNoYoKiqRQx9GroOi7klmhA1ybdu2lVUrVhlDbZPZdnundOrU2dO3f/8+qawcK89sfsYL409Gmwxv9IvfGsI3it59510/XQ+UgBJQAkpACaQTATWA0qk3tS1XFAEYQMfMQ/8F82HNs1/U7IzWzHw0s8x8LBRGAz9gmUoG0Ljx4+Svf/2LtGvXXpoZA2Lf/rARVzW5SmBRPGsZN+zQFs1byLy5c+XQRx/JlxdDEQYQZIYOG2pGTU7Knr3Y5SzSYbOCUaNGy3MvPCtDhwyLMIBgmGC3tJu+8tU6G0APGOMmNzdXjjtbgw8ZPFTe3PmGWXNz2q9IXQ0gZGxtRrxKjGGLj5G6LpYB1L5De+lovjH06qs7/Gy9e/cxUwzfMd9AuujH0WBCxASzHfYL1dthYzQIxpIaQD4qPVACSkAJKIE0I6AGUJp1qDbnyiOQk5Mta9Zc432j5/4H7o+YekUaqWAAcWoY6oTd3bZt22amaIWNH9azqmqSZwCtWXOt+cjru5KRkSE9zdqc//jNf3gG0P0P1P4WEPP27Gm2eTYG0KqVq+W9996T1ibvgP79zSYEv/EMoA3VW4NTfpgxmnaaD5J+efFL+eLsFzJy5Eh5Zcd2mWi24O7Xr7/89Gc/pWhUv8h8G2nx4iWm3L2S0doYLNWjTi+++GJEnvoYQFDQqbMxZI0BdOut35H/83/+t6dzuvkw6aPWh0mDdA8fMdz7IC5Go7Kzs71pc2+8/oY/XQ6KbAMIYeoJSkOcOiWgBJSAElAC6UJADaB06UlthxJIYQI9yrvLPrMeZdWKlfL8X/5idn+rkIf+GN4u+3JVG9tZf2A2PLDd4UMfygWzEUKxmWIGA2q3mTZ4JThsAmGG37ymlpf3krd2xv+o7JXARduoBJSAElAC6UlADaD07FdtlRJIKQIcXfjPP/hP8pN//peUqFuQAfT+++F1Lx07lF1RBtDo0aPk1ddelcKCIrOurGZDjZToKK2EElACSkAJKIEGJqAGUAMDVXVKQAnUJgADaKUZ/elu1i257r/+139yoy5bmIaaOz3sslUoyQWvvW6tWUd2TDZt3mQ2bzgtpSVmR0E1gJJMXdUrASWgBJTA5SagBtDl7gEtXwlcAQRoWAQ1FZsQYA1OKjjW80oxgIYNH2Z2ynvVQz948BB56cWXUqEbtA5KQAkoASWgBJJKQA2gpOJV5UpACYAADYsgGmoABVHROCWgBJSAElACSiBZBNQAShZZ1asElIASUAJKQAkoASWgBJRAyhFQAyjlukQrpASUgBJQAkpACSgBJaAElECyCKgBlCyyqlcJKAEloASUgBJQAkpACSiBlCOgBlDKdYlWSAkoASWgBJSAElACSkAJKIFkEVADKFlkVa8SUAJKQAkoASWgBJSAElACKUdADaCU6xKtkBJQAkpACSgBJaAElIASUALJIqAGULLIql4loASUgBJQAkpACSgBJaAEUo6AGkAp1yVaISWgBJSAElACSkAJKAEloASSRUANoGSRVb1KQAkoASWgBJSAElACSkAJpBwBNYBSrku0QkpACSgBJaAElIASUAJKQAkki4AaQMkiq3qVgBJQAkpACSgBJaAElIASSDkCagClXJdohZSAElACSkAJKAEloASUgBJIFgE1gJJFVvUqASWgBJSAElACSkAJKAElkHIE1ABKuS7RCikBJaAElIASUAJKQAkoASWQLAJqACWLrOpVAkpACSgBJaAElIASUAJKIOUIqAGUcl2iFVICSkAJKAEloASUgBJQAkogWQTUAEoWWdWrBJSAElACSkAJKAEloASUQMoRUAMo5bpEK6QElIASUAJKQAkoASWgBJRAsgioAZQssqpXCSgBJaAElIASUAJKQAkogZQjoAZQynWJVkgJKAEloASUgBJQAkpACSiBZBFQAyhZZFWvElACSkAJKAEloASUgBJQAilHQA2glOsSrZASUAJKQAkoASWgBJSAElACySKgBlCyyKpeJaAElIASUAJKQAkoASWgBFKOgBpAKdclWiEloASUgBJQAkpACSgBJaAEkkVADaBkkVW9SkAJKAEloASUgBJQAkpACaQcATWAUq5LtEJKQAkoASWgBJSAElACSkAJJIuAGkDJIqt6lYASUAJKQAkoASWgBJSAEkg5AmoApVyXaIWUgBJQAkpACSgBJaAElIASSBYBNYCSRVb1KgEloASUgBJQAkpACSgBJZByBNQASrku0QopASWgBJSAElACSkAJKAElkCwCagAli6zqVQJKQAkoASWgBJSAElACSiDlCKgBlHJdohVSAkpACSgBJaAElIASUAJKIFkE1ABKFlnVqwSUgBJQAkpACSgBJaAElEDKEVADKOW6RCukBJSAElACSkAJKAEloASUQLIIqAGULLKqVwkoASWgBJSAElACSkAJKIGUI6AGUMp1iVZICSgBJaAElIASUAJKQAkogWQRUAMoWWRVrxJQAkpACSgBJaAElIASUAIpR0ANoJTrEq2QElACSkAJKAEloASUgBJQAskioAZQssiqXiWgBJSAElACSkAJKAEloARSjoAaQCnXJelfoZatWiTcyMLCIjl86LDYec6fu5Bw/lQX7NS5k1y8eFFWrlgpt912W0pWNyMzQy5eCDNvDPY9ystl3749snjRErnvvvviMnHlEz1XEpWLW4FGFmiT1UYunD/vl1rXPmG765rPLzAND9p36CBHjnwioVCoVuvGjK6ULVu21IqPFZFujN3fWKy2a1rDE0i388kmlM5ts9upx6lHQA2g1OuTtK9RWVlZRBtPnz4tJ0+d8OKKCoqleYvmfnpRUZHs2LFDDSCfSOMe8ObUrVt3+eCD96UxHprr+rDlyrPOIMX6Dh8+XF59bYegHW/vftuDGCTXuHTrVxrrHa9Ppk6dKi9v3ya5uXmyd89evzDmJxs/IUkHQeyTVFSd1fbq3cs7r5mxrKyTzJ0zW355++0ybux4efa5Z01SSDLbZMrx4+FrFGVj+Y3NOFZdGiLN/Y01hM501JGsc70pnU/9+veT/fv3S3l5T3ll+/a43dyU2harMaNGjZLtr7wsHTp0lIKCwoTaHktfImnJOt8SKTstZMwbL3VKoFEJdOzYMWT/Hzl6VKhFy+b+fztt0KBBXt3s9EatbJILK+tUFmrfoX3ou9/9bpJLqp/6pUuv9vulfhrqnqt7jx5emcuWLUsosysfdK4MGzbM09mzV09fZ5Ccn5iiB3Z/2G0Jqu6UKVNC+W3zQp27dI5IZrsjIpMYCGKfxOLqpJosWrZsEerXv2+oa7euoW9+8+uejkmTJoVatW4VatmqZZ1/A9Rbp8qksLD7G0vhql7WqiXrXG9K51Pffn1D2TnZocFDhiTUF02pbbEaNHLkSO86gettom2PpS+RtGSdb4mUnQ4yGPJXpwQuKwHXAAqqDC+S8NPJNRUDCA+CjeXq+rCViHy63ChoACXSH2oAxT5jZ82c6T2wdOjYIQQDKJoraFtQZwMomq6mGp/Ib6yptq0h650u15lLYVJXA+hSykqlvGoApVJvJFYXNYAS46RSSSRQFwNo0eKF/sOIbRQFGUYlpcWebPMWV0X44yeMT6g1M6sfkNxyEJ41e2aEDsq0btPar1/3Ht19GbwVogz9HuU9QtEMoKLiolrylZWVvj4eUFeGVW6fvn2YHNUfN25sLf3jxo/z5anX9X2BGAd5ubmebpd7jnkraDu8JcvLz6tVj2gPW2Dl1gdv7F15W2bixIm18iAdzpaz6/X9733Pe4Npp+N4UtUkW8zP3659+1DrjJp+t/NFZIgSmDZtqqfL5TVt+rSIHLZeyiIuyCXS7ukzpvltoG4zHSVIXai0XWktWeSBkRXLRasHy3Prz/h58+dGqC3vWe6VP2XqZD8+UW5+BueAZXGU2Un2g9des8Zvux9pDpgffuuMVl64S9cungjTbHkcB/EYNXq0r4vyyN+2oK0XtEegounNzc3xdVAGfnZ2FlV6PtNg8AVdq6Jdp9zfWIRSKxCh32FCsbqcS4leS6A7mO3IkJnm6LFh+fRx/W2TmRHib4m+e39Am9AXQf2ANLhp02r/lpiGdJ6/5EM/o00GkuM6ytuC3bp389rFetPHvSARB53R2hWUP97vbdasWYHnIMqJ5dy2MdzCnKM1x+EZIpOqqkIY+Xbj0fe2Gz0m/JuqHDumlizygp3t4rXNlmXZrarP7yHDhoYqBlQElmPny8mp/Rt1f5+Qh370S6vWNSPPLBM+XbxzjnLqRyegBlB0NprSSATqYgDhAlBYWBjKzcs1N6/M0NixNQ/y7dq382vMCwYe6HAhadeuXcg2KsaMGePLBh1MnlzlX9Bwo8RNu39FhZlO1MWPv+baa/ysKK+gsCCUk5sdwhtlPBh26tLJSx8xYoSfJ8c8qOBhuUu3Gj1dunaOmAJn172kpCSUmdnGtDn8Fnr48GF+mTiAbBuTjml02TlZoekzZhiDoMbwihCuDoytNn5gPPTt29erZ6nhA10zZk73pFiHBQvDBmd+XthQCdLHuCVLloQ6d+7k6Zls2j9u3LjQCDMtAIYD9a1Zs5rioR6mnojPzGrj9REeMMymEL7s5Ck1D7sDBgzw4sEuv21+CA8OPXqGp8rxxr948eKIukM3H4oGDx7s5eeDHARZJ/h0br8PHTo0BEPa5ePmhyHXxZwbeKhEHuouKiqk6kB//vz5vmzffv2i9gfLc/vDrrtdANqN/3n5uZ6RzfpQD8P8LQ0dOsSvR3Fxsa3Kj8dvKXwuFvq/pc7mHL/66qsj5O0A6uCyR9mVleEHExgOdHPmzLHKasloz2d9OVLjcuMDD3/j3//b70fkdwMDB4XPJ+iNZwC5eRlmnTqWdfQMIPzm+dtjGmXtFw48B3G+l5ZGGpaUZ374/O3j3OLDfL453+g46oAXGL169w5NmTw5NMS8XBhS3afTLUMa+tzrBeLwgB50nYr2G2PZrh+kn0wgi3T8t8+ldpZxPXXqFF8leFJ+wcIFoRnm2hbtWuLyjcXWrUeeuZfgf7R6sA54KMVx0G+cD6Puuc7GUAfOFbSrpF2J36+oazzH/JRjGD76HdctXIN4rtRFJ3SUlBR796Wg88u9Jka7F9IA6m3OQdyLBgwc6Pcf6x3ksy1MYxg+7qW41k+cNNHXhXjc63EtWLp0mR9vj4r3r+jvx48dW+ndH8HcNlTQVjj3WoLfDqYOo2zWZf6C+ayeF+f+hqZNnx7i7xAv6th2ZmIa+or3xaDfJ+RZJnz2S9A9Beece74hj7rECagBlDgrlUwSgboaQLYRAAPIvjiwingQwMUABgkdHo46d+4camMuqPEuFEjHfxg/trEEAwgXpXB6zdtyyuOiTAOI5TKth1nbAgMIDgbQyJFhw6iwqMA3gOx622/j7Qcl6oVP3SiXBpCdHnTMPLhJ0AW1CWmcctXWGB3xXHFRcYhvomfOnOGL46GFb0DtMlmPTuaGQTdh4gS/TfPmzWO0HweGMIDg8HAWJE+98Ol4A7LXzQTJMQ79jv90QXwoCx/tggEEh/ORb2eRFstRB/LDAKILKg9pdekPPGjFWgPUp09v88AUNtBgAPU1I4esD+sB3z4nGY/fUqEx7iBPo4Rprh/EngaQzQcGOcu342+6+Sa/nyuMIQxHOZdbYUH4RUG8B0AYedTh1jfRMPPDBwPwpmOaG0Y8zlk6+wUO0uiYv6i40HuJwPig8yo/P99riz06BvlYvznoR53xwoSOZdrXqWi/MeZxfeoI0g/ZoHMJhkfQ9c1uFwwguHjXkkGDB3kjwpCFTr44QX3o+piXPghnZWeG8gtqrmvR6sE22aMG0X7jQee62RTAK68qygjy2rU1L9JYR9dnHRjfkDrRLlxv4GAUcISOZbFs+AONUUMX7V5Y1ylw1E+9DA8aNNC7lyJ+8JDwCyyvDmZdMF92wgBavXpVrd/yUDMqQz1Lly6h6tC8+fNCOEeYhgQeu9eSdhEvJ4Lv9fY9N9YUOPtcZmWCfp92fex+qcv5Rv3qxyegBlB8RiqRZAJ1MYCWLFkcsg0gVI0XMPhwJaUlXhxudLYBhDQYQJXmjRBkMWoSzVEn3p7aBhDkR/mbNtS+KOLi7zrqwhsb2/GiaG+CYNfdlsXNPKje1B1Urp2fx5RHu3DBp8MNMKhddXng/va3vx3C/1tv/U7INoBQBsvlgynCxSVF5ua1OhTNAOImCMwLfng4s11hQfghHDKuPOLogh5MqJdyDGM0Yc2aNczq+UF8KL/AvB20WSID06g7QpkVoJz9lh7JQeUhvi79Ec8Awm/JdqyLXWf7fHR/S7bxiY1Lorkg9pClwTPcjJDC2eXjmFMy7XjXAHK5RRoUNb9PrwDrD3Xibb7r5s2bW6sulIdPx7juPbrVMgKZ5soi3jWA8AAcTR7nFkZR6YIMIP7mXANo1cqV1XprOLAcXC9cw5Vp7nUq6DfG+rg+dQTpj3UuBV3beD35znciN4hhGfa1hHF8wcR6BbG162EbQMgTVA/oxssq2wCCLMuETxd0rlOuoiJsvFOWxiBGSeM56qAcww2hE+eY7aibcQzjumgbQEgPumeg7y9lEwSWh2sdnW0ATTKjQbaj/IqVy/1ojggjzTWAZs2umaqHDMzvXktgANUY0MG/Ib9AcxDLAAr6jQb9Pu36ROsX1Jcu6HxjmvrxCagBFJ+RSiSZQF0MIPvHz2rxAhb0AMy0aD512D6mWkAe88/diyLkai76NRci6ncNERhPSMOQuftgAV2Y8mUbQNQTz0deOMq55YZTa/+12+amUhd8uro8cPOBBQZQhZkuiBEsTk+jj3ndcL3N6AOms8EAch3fjLE/bYauLMKufFA7gm4UrpzNxjWAUI4r74YhQ8c0toHxtm+XF3SeUQd8urr0x6UYQJyqaNch3jHr6PpB7CGTlZPlM0UY+vFGdVz1tNZrq6eYupsQxOIWaQDVcIN+22FEk+2x43EMAyjLrJ3B/8ysTM+3pwFRnvnhu45piOcUmzwzjbS0pNQV9eJseQgw7D4E2Wk8t/hwhWsA80X6tR/ekG47+zcWdJ1yf2N2XvvYLteOx7GdFuuY+Xg9iXctwZReTKUMYgsDiC+aqDdW2XaaK88wfcqyHxAfdK6Xm5FqTO2jPHxcG0cYoypRx7yUn1l9j2K8p9NM9R5t1pMl6pjXPccYj3bNnRuelpqTnR3C6Krrgu6FyTCAUC7rBcPBdozH6A4dDSCMlLnONoBWLF9uposODmWZ33mi12CW595zEzGAcN9j/hq/5veJujI+Vr+wTUHnG9PUj09ADaD4jFQiyQQa2gDizQZzeTE3N9b/oKZxioQ9XcqV40WK0xcYduU6mREnpEUbbcLbYxpAWH8DWazLiVVnpNFFK5fprh+rbdQFn64uD9zdu3f3DD3qwVSDr33tFq9NNQvJwxf7YjPihDVTQY4PcnywiMfQlWf5djuCbhSuXCw2qKcr74bttjCNbbDTeFzX8pCvLv0RzwBiPeizzvBpAF3qbwm6g9gjHm++URaMDGw8wfJpAHEKKOPxoAJXH25eRusPHpao14qOeshNDpCHjvntODcNYa6tKevU0VuDQBn6XbvWTP1jHHUzbPtM47mF0ULGYXQDmyrgd+f+5qCDcvBtV9ffmJ3XPo6mHzJVk8NrAVG/WNc36rPX5OBcwIjgN7/xjVrtwtRNGKtY3xHkOOKDtPqcz2yTq5vx7AekRzvXUS7qEfQAnGmm4sVzLItyMIA4VQ0P+1gTSxn4WFcZz1HelWM82oWRbYRjbe1Med4LG8oAilavaPFBBpA7e4N5WWeMGmHNDqatBznKwf/qV2/0RBjnyscygLg2EXkxzfCWm2+udR5TXzT9jE/kfKMu9WMT0A+hpsXXnJp2I0aNGS3bX97mN+L8uQv+MQ/MDZCH/sctGcG0xYuWyH333Rfx0dSqqikUC/Sf2LChVvwNN1wvd919lxcfVBcksEymu2EqXbZ8uTz00B+i6kK+4uISWblipby58w3ZuHGjJ5tovaOVy/JdP1bbqAt52K5ly5bKQ396SHKyc+Szz4666iLCzF9YWCwtzMds8RHbyjFj5Be/+Dcxi0hl/frHjHwzo/u8mLe28uKLf/XLsRVRD/szEYbIT3nmRxzbEfTBOFcuFhvocuXdMGTomMY6Md7261oe8talP+r6IVTWGeWsWL5C7rrr7og2J3pOIr/tgtgz3SyQNx9N3CfNmjXDyzhpm1cgH3/yscyYOUOefnqjtGrVWs6d+8ITH1AxQLZvf0Xqw43l0a85H8MxPE+Y7vo2G8oGxTEf0yBrNueQR9Y9zCT/nGQEZRF2dTNMWfiUx7n1x+prS7t2HbzfHD4qjQ/kDh0yWA4cPBjxm7Pz4tjWXdffGPIHOdYNabZ+hO20WOcSrslmepvJEUI282HJMjl06KCMGjVaBg8cJHvN+WJfS2y9bpnIz3Skmd2+ZPMzmxEtseqAdN4b7PyIp2O8/RuPda4jn9mhU957712ZN3eBPPfcVvns6GeeuqB6sxz4LCtIbkzlGNm5c6dMmTy1QXSyLLTLjJTKr//9135VgsqnPNMu9UOorj4WHi9+1qzZ8vCfw78zMNm27SUvK+tFPfCpy2zgIh9/9LFs2bql1vlqy+GYepiXYaTBRfsQKuX5G23VqpVMnlQlBw99GHEeh7XU1M3VTz11Od+oU/0oBGLbR5qqBJJPoKFHgPjGL8NscRrkyswbH7xNcddtUPb666/z36ZhlxXX8U3MwoWL/CTG+RHVB0vNWzSmuSNKnF/cp29vfxOEWHUPqjd1u+VGC1M+0XbVZcSBuuG7riYtPAKEcLR54lyMzykJzOvyQxl8uw4ZjlpQHj5d0JtZV45h7GIUNC+f6ex3huG7jmn22zpXpj7nWV36oyFGgGKdjxw1QFvdtQF2W4PYMx15c832sNhlCccrVoTn8eMYGwBUVU30pol+/evfYJZQLG7Ix/9Ll8b+kC7l4Mdy9g55tmys/EyjXobxm3edeVHg15lplGfY9pmGc4vH8F1Xk1YzxaYmLlI+1nUq6DfmlsVwNP1Ij3Uuudc2Ww8W29uuJq3mWsI4TIG0XRDbutQDuqjb1mvH27/xoHP9uuuu9XSUdQrvCko99sgd46L5dh2i6UPe+uq0y2VZaNfNZgMShnFddB3TeE1EeiqNAKF+ruMnC9qbneTg2IZY98Qqs/02HeUZph9tBIjybl1q4mt+n9DFeOqlz/h45xvl1Y9PQKfAxWekEkkmkAwDCN/CwQVjzpxZEbXHwlnEY9pZNAMIGTjlBfK4YNJxCgV0YNtnOl6cGLZ9lgkZ22HbTsTZu8ANHzHcvwDeeMP1vji/iYDvjNj1jlWun9k6gFHBttnbhmJjCejCg799M6vLAzfr4k6/AGumwYcbYdpp3mj58awib06Q4y5w2D0pGsMgebcs6MYCccazLIbhw82ePdv/9gLKs10QHze/Lc80+2Zlp/M4qC+QFlQe4uvSHytXrvCMCLYP+eFYt3Co5i/j4dOYxMNitN8SzknspIUpabEMoCD2LHXc+Jpt7O0pkfY3uLCNvW0AIW80bhXVU3ZuNlNM4hlAZpQpYotwTPNxHb4TAx4wvrE+Ccd0Ni/G0Wcaw6wv4nHe03HtjSvvhikPn2k4t3iMKWC2C/rN2XmRz3V1+Y25eRlmfYL0xzuXkIffUcIGDdQF7nRB7cLOcPxmSiJs7a2QlyypeYmFMuzrLMtkPRimz3j7Nx50rmOKJ2Td84svEMwoC1VG9VkWBGAANbROu2CWxXbZ5659z4h2Lxw1aqTfd7beaMcsj+luONF4ewqcvQuczR2fZ6B+nldsn902lGn/NvkyDvHMj2PbYeMfpsGnY5z7G7WnxVEWPuXtODue/YK4oPMN8XWd4os8V6JTA+hK7PUUa3NDG0BoHm6g9gWGFxX4+FCcbdQE4cACRPsmbOfHMR7yEzWAli1f6l/UbD24WU8wH2XFTf273w3vdAQDKNoHXDGi5dab+oLaEC1ulrlQB7UND3t4G2+7ujxw9+7Tx1sDxA0P6OPGwodHu7582GAc/bnVu3DZF3ouxqUMfTB05ZkGnw4frnXj3TBk0e+tqo1kOx3HLh87neXQZ5rdBqbZ/ipjpLAvyIt+G3OOXUp//PjHP4poM+oEx7rZ9bDjkU4DCPGoX6xzEgZQLLdwYc23jtyybQOI9YMu2wCy41lOPG4wgBJx+E6TO8LDOtJHv3PHLrsuTLfjWCbTGOZDFgxGptG3jXjKM41h22cazq3Zs2Z5WwIjjucNffzucJ2iPHTwGL7rYl2n3N+Ym5fhWPohE+9cogH0rW9+y1/jYuuMfi0Jb2tty+IYayxpHLGOMIBKzTdhXFmGcZ1lPZCH8cxPn/H2b5xx9CELY6V/9VbYjLf9Kda3j6jb9SnPeM4eYLzr83tulA/ymcdNYzzbhWsi4mJdp4LuhTwPkTeWY3mUccOJxtsGEDdBoK4gnwZQvGsJNn9IxACKdp3Db5Trtex6hH+fkdcDtJUybDd9xrNfEL96NXd6rBn5RrwaQKAQ36kBFJ+RSiSZQDIMIFS5qvpjpt/7/ve8jzV+62++5X3sbt7cyK/MR2seLvhYoIwb6I033mh2xJkbuuGGG7xpV+4oBy9O0XQhHTvBLVq0KIQ38//pBz/wFl66BhDy42ET8Xa9kX+w2VTAdfHKdeUZpnG40uyoc8014W14Kysrmez7dTWA+IYNnLgBAnYmimYAgQnagBvot775TY9JtIctPszZDDF1xpUnE/i2g+HLNMTz2JWDAQQ+dp9DxuUTLb+t275Z2XWxj3GeJVIe8tSlPyCPOkZrN9JtZ7fHNoAgg/MR6fY5ifMx2jRTWy+OIWfrt9MxZYZpdry9YNyO5zG4FZiPU9r9hI1PYDjWxcEAmjJtmvfBReiabbbJvfGGG72RmunTZ3iG7y233FKrjqwzfNcxzY3Hx3ox0mXWyHn6OArgyrthWw/TeG6NGx/uG9T9K1/5ivcyBVOx8IBFWfhwbtjWy/Sg65T7G3PzMRxPP+QSPZfw0IgHWbBfvnyZ1y5srBJ0LYFeGJf4GCe/84ZvxcAAYp0gQwcD6Ktf/aqnyz6nMYLontNB+aGH8ewHxrm/N8TDAMJOathdcsrUqaG1a9d6+b0Po9bTAMrJyfZ0oB1o96pV4e/h4JrYkAYQ6g/He4b9e8M10f29gUus33tYW81fcmSMG040PsgAwouLbDM6+vVvfN27d+MeglkOKMN2dbkGR6sf9EVrd7T7InXRhw77GGE6xtvnG9LAn2nw4dQA8jDE/aObIERZG6XR6UPAfBVe9u7ZK2akRX76f39ar4aZBwv56KOPpKSkRH7965pFoXVVhgXRGRmtpXOnzvLf//VfY2ZviHrHLMAkmpumWTzdQu688854onVKNzdJad26lbcBQiIZsRi1Q3vTPz/7WVzxujCMqyyGQEP1eYwiIpIau7yIwhMMNMY5mWBVfLGG5AZdh8zi5PZmU4E7fn2HX0YyD8wopqc+MzNLjh87Xu+iUHdsJpGbmyu33XZbvfUgY2P8xhI9l772ta/JUbNZQMeOZfVqF/hiM43PT30eyCTRegRmrmOkedkkhw4flrKOHeU3v/lNHXMHi990001y4MABs2FBW7nnnnuChRowtiF/bw1YrQhV3AShe/dy2b1rl3zjm9+Qs2fOxr13J7ttdb0vRjRKAw1OQA2gBkeqCpWAElACSkAJ1BAwb8rlpW0vehHnrV0uzcdg5eDBA1786lVrGuyhuKbk9D8yI/Oy4YnH/YZG42vH+8J6kJYEXAMoLRupjbpkAmoAXTJCVaAElIASUAJKIDoBM63SSwxVb+3sSvboUS673trlRms4AQIwgJ54YoMhG942280CtmVlZfLUk0+5SRpOUwJqAKVpxzZws9QAamCgqk4JKAEloASUgEsARlDnLp1lbOU4842eA5KdlSWdzFTY//jNv3u+GkAuscTDZLt37165eslSOXLkU+97SHffc5eyTRxj2kiqAZQ2XZnUhqgBlFS8qlwJKAEloASUQA0BswA+wgD6+c9/XpOoR5dMwGzs4htAt99++yXrUwVKQAmkJwE1gNKzX7VVSkAJKAEloASUgBJQAkpACQQQUAMoAIpGKQEloASUgBJQAkpACSgBJZCeBNQASs9+bXKtMt+sMN+k+tKvd9COPdwuFkJMN1/FlnvuvVdKS9vJgf3h3ZR8JfU8YDksI5oaV84Nx8uH9HhlQCZRvZBVpwSSRYDz6keOGCnPPfd8soppUnp7lJfLvn17ZPGiJXLfffdFrTt/wxBI5DcfVVETSkiUTRNqklZVCSiBNCKgBlAadWZTbUq37t3Mdwz2+9Xv0L6D7N27zw/zIOghItUNoOHDh8urr+3wFuS+vfttrylB7WAbg3zKXykPTkEMUjEuqG9TsZ4NVSc1gGqTTPQhn79haEjm73jq1Kny8vZt5ltAed63z2rXuPFiEmXTeDXSkpSAElACNQTUAKphoUeXicCy5cvloYf+YEpvZv6HtzLFhzF/d+/vI2oU9BChBlAEIg00IgE1gBoRdooWlehDftC1KxlNUgMoGVRVpxJQAulIQA2gdOzVJtYmPhwMGzZcWpsvdj//wnNeC9w3pZRDItNSyQAKwh70kBzUjqC8GpfaBIL6NrVrfGm10xGg2vwSNYBq50xOjBpAyeGqWpWAEkhDAiF1SuAyEmjZskWoRcvmodlz5ni1yMjM8MLwXQc5/mfa2rXXeHEdyzoyyvMp165dOz9Pz149I2QYKOtU5sm0yWoTkZfp0XyWwXQ7PG3aNL9cxsOHY3j6jOgy1GnLM27evDm+DsbRp26W5eZvUc2bciNHjQz17dvH18d41D+eoyz6sHWb1r6O7j26+1lL25X68ZSHP2XKFF+GB3m5uZ5s8xZXRfg5OdkU8f2JEyfW0jtq9MhQr969vHhf0DooKi6qlaeystKSCPdNbl5uqF379qGWrVrWkqdwUPloF12Xrl1q5W2d0ZrJcf3KsZVefpcFWNsuUWZkH69dtm73ePSY0V6dKivHhMp7ltdqX3FJsZslVFJaHNiO8RPG15J1I/jbtrnaMmyTHdepc6da9YrGvS5169qtay29BYVtQ9179PDily1bZlej1jHrarcFx20L2obM+sdaum05Kot1Ts2aNStQh60nqL34Tdx8880swvcTPa+YwXzfqFb5ibKhDvWVgBJQAo1JwCw8V6cELh+BHtUPEKWlpV4lpk6d4t9Ih48YEVEx3Mz5nwl8SKIBdNNNX/Fl8MAAA6iiYoAfx3z0r702bEBB76zZs7xotwzKur4rZ4dpAA0ePNgrmw8D0EE5+IWFhSE8cBcYf8CAcD0LiwojiqI8I+trAEFPSWlJKKNNRmjipEgDol37sKFYVVXl1Q8P//Ec9LXJbBNq36F9KDsnKzR9xgwvLx6O4VhvM+IVyjRyaGs7yyBCX9MNGzbMkx83flxo3LhxoREjR4YmVU3ydaxZs5qioRkzpvvxffr29QwVnD8sZzc1WAAAEEJJREFUD77rmIa6xKoH5eAXFhaYh9OW3gMqDav8/DxPNQwgt29Zrq0Dhl5JuxJPF+IT4TrKGKWQ7WUM9oqKCq++s2fPNnHhlwX5+fleHaCbZS1YuMDnNmToEC9++vQaI5Zy8EuMoRKtXS43Ozxi5AhPL42yQYMGGUOxXch8hDLElwg4F+hYJpijPPwWO3XqFMrOzvL0jBkzhqKBPn/b0BPkqJ9pDBeYfsN5NHlyVVTulLXrlmd+h+hzpA0fPoxqQyPMdYjyObk5IRhUXbpFGrgzZ8305YMOmB8+nR2HY+gdOnSoX1aRdR2wZYPOKRpAOC/z8nP9/mB5zG+3134hYPdFXc4rtIUvULKyM702oCzbEJ08ZTKbrL4SUAJKIGUIqAGUMl1x5VVkyZLF/s0ehghd+GEvbOwwDj5v4rypI44PSTCA1q691pfp2bNnCAYQHR6ImJ9x8Bm3cuUKP5pxfkSUA1fODSMbH+zt0SfK4WHYftCyH37sIinPuPoaQHjAYnm2AYQ30HiQhVu9epXPhOVF81kv+BiZgAFkO6bn5NaM4MAAwkMY0yjP8JSpNQ9LMIBWrVzpybbOaEVR3/CAXhhAcDCAMIJHPb6wOWAcfJQNF68eaE+5OYfozEYdvh7GBfUt0vCwj7KqTP3p8GCNc7R/RX9GBfpDhoQNZpwbMGTorr/+er98sz7Oi7bbBQOILogZZdEuuw5B7aIe1x83fqxfh8GmnjCA6KCTZdBAY9jufxhAtrHK/EE+f9vQE+Son2nkzjB8cO/Vu7dXNxgHdMxr1w1pQXXjyBfywACCgwG0Zs2aUF5enqfbNjY9AecPy4NPxzj0CYxSOPsaYMuybfHOKRgv+W3zQhiRsR3LstsLAyjWbxF54p1XNhu8zKKbMHFCwmyYR30loASUQGMSUAOoMWlrWREEeFO2b/QQyK9+qHDjg+T5kLRi+XL/AaxiQP8QDCDbZVW/dcb0rFGjR/tJnTqHp25079HNj2M5fkSUA1fODSNb0EMy5eC7jmkwROgYx3B9DaBbb72VKjyfevHAbDvEl5pRi5tuvsmOrnXM/PBdxzTbsKQMp3fZ+b797W+Hbr31OxTx/ZqpVjVTv6jbfphDBp4Ltl7KwoeBbLugetjytiyOmca+CepbyJV16ujJ0thEHFwiBhDLgO86lscRNjDD/+9857sRorGYBellmWxXhDIrwIddjCLCAHId9dh+UP8jny3j6mE4qD+ZBp86GBeNu2sAMV+idaN80LRQptV3ChzyL1gwn03wfOq0+yNa29xzKsgAor6g9s6bP8/nCDm4hj6v4rHxCtU/SkAJKIFGJqAGUCMD1+JqCGBKD95s4k3/goULI/4PHDTQuzHnVU85Qi7eyHmjRpxtDASlQwZu4aKFtfKbDRT8uFQzgOyHBrYr3JLINjOOPmVtRoyjDH3G27JIQ7ihDCC7jKBj1oU+pnzhrTSnWdHHuQKHkRCsZcCb9yCH0Qe7PUFlBsVRl53GOPpMY9/QILFH9yBrT+NEHrQH08cScZhKxXISkYdMPGaQoU74rmMa2+WmM0wDiFNFGU+feuyXEYyL5TO/69fVAJpg1hW55dijaNTvysQKY2oY0jHVM8jR2IzHzi6DehjHMH3G2zoTPadiGUDUG8tnHeAncl7F4pMoG7tMPVYCSkAJNBYBNYAai7SWU4tArBuxncaMQXH2RgJch4A1NUGusCA8v7+8PLxGhQt3Me3IdizHjgs6duXcMPIEPSRTDr7rmGY//DCOsrbRxzj6lLV1M44y9BlvyyIN4Us1gKom16zfsctxj1mXceNrP7xCFg+w6E8aQOONHNY42GtNqAN+NzOSh3x0EyYG641WDzueOugzjX0T1LeQxcMqRkkoT3+oNaWNOl1/4KDwOrDM6g053HQ3jE0sqJ8+FuyDD5khD9Pgu45pbJebzjANoNVrakYnmQYf0/aga/78+bWMQJYR5Ns67OP6GEDcdIOGM/0RI4b7ql1jIqhOjOM1AkyDHNdrxWNHffDpGMcwfcbbOhM9p4IMoLq0l3VI9LyKxSdRNixTfSWgBJRAYxLQbbDTcGe/ptAk81bcq2a/fv1l5843a1W5WbNmMM6lRcuWcubzM1468yDAbbDnz58r6x9/XMaMqZSioiLZtPFpOXX6lCdPGS9g/rj5b7jhernr7rvkqquayxdnv6CYL+fm9wWqD6iPcm4YYkFbJVMO6cyLYzim2V+WZxxl2WbIMw7HcJTFMdMYxzDS4BiPYzsN8WajAFmwYKHc/svbkRzoouWHsJ1WVTUlMD8in9iwQRYuXCiPPrbOkykr6yStWrWSyZOq5I5/v0NWrVgp9/7+dyatmanjebnpppvk4Uf+LCdPnpTPT5328th/zO6BcvHCBb89dakH9NjyNhM7jX0T1Lesi3kQl88+OyKdOnWWwYOGmHP0Mblw4bz3gcojnx6hWC1/ypTJsmXrFi/eLd8VNsag/OWvL0hxcYl8+uknMmrUaBk8cJCcOHE8ghny1aVdbjkMcxtss5ZGnnpyI6N93y7DjzQHsfofcjgHghy3uEdaEAuWZ6eZtWzmo8PdzDVlp8ybN18eN9yPHTsmuJ4UtC2Ujz76KIJFvLp9fuqkvPjSiyb/VXLui3O1qmk2KpDjhjfPiVoC1RGsK4KsL+MYZl7GuzoTOaeCtsGmPuiP1170RV3Oq7FjK6PySZQN262+ElACSqBRCTSmtaVlKQES4JocLFIOcpxawfUOkOGbUfstKt8SYy483HDzppdyq1fX7ByGtN59wouhmU5/0qSJSPYd4/2IKAeunBtGtqBRAsrBdx3T7Le/jKMsw0H5+/Xv57fflWeYfjQ9iL/UESDqxhqDIPf3P/y7EP7DURa++6a9rHqLco5mfPWrX/Xlg/RSF9MYhr/YbLrhOrseSLPlXVmmsW+C+hZ5XJ2LFi32dt5jflevHaYMfNdxBIbTuihbZjYWsJ3LDGmUDdLLNLbL1mUfs/wgHZCzNy+hznj9/6O//6FdRMQxf9tB5QWd5y731WaTgsKi8Kgv64MCeJxI3Zaa7a0pH1G56gDT4rGjHHw6xjFMn/G2Trdt0c6poBEg6kukvagD5RvrvGK71VcCSkAJNCYBnQLXmLS1LI+APb0C6wWiub79+no3Y6bzxgyfjg9JtgE0v3phLxYOu27KtGkhbNeKLaexW5Jr/ECe5bh53bAr54YhP6zaIMNmC3SUg+86ptkPP4yjLMPwsbaJDt+0sdMYzziG6TMevu0QvlQDyJ4C5k6Zcst1w6xL5I5YNZsgRNvRLyje3nZ7dvU259QfVG5QnCvPvgnqW3tdGfPRp26Gg/zFixb5fWinr1q10mzeUTPdDWnR9HHLbhqNtizyuI562C43nWF7Fzhse247e0dHbD8dq/+Rj2XaO9LZ+ngMOei68StfYZTnVwyo8HUgIhHubHtd64ad11jfiEqYAOMvZRe4aDrZH4m0jTpwfctvm+/v6oj4WO1l/eEPHDjQU8M46qQfdF41BBvqV18JKAEl0JgE1ABqTNpalkeAN1j4sRy2baYs5Hhs53MNIMjBGKKsmf6BKN/hAcHWi22AXce8brwbduXcMORnzQ4vas8zxlaVeTCEoxx81zGNDz+2PGVvuPHGUFFxoacHH1JcuWJFaI75kCweeLEDXpeu4Z3tKE+dDNNnvFsPhC/VAEIZ2N4XuvBdlpVmpznUE/VFHPqA25TPrv6II/pq7tzwB3F79Qp/0HRk9bdnMLJHhy2xoQP/O5utzufMme3pxfdl+MFKysLHt40i6hKlHpClXviuYxr7ZuHC+eG2mI/A4lsx/N4J5dAeyiIN4SC9djm2AYTvwIDZ3Hnz/BEkbAoC4x3O5dbXbAkO/TSEi0uKvK2aIcs6BZXPNNYV8kFu6LDwN2q47gNbpy9ZssTblpzbNOMbU3QRzE3/rzEjstjumetycA7Ec/z2EOoIo2ft2rXe+qa2BfmhYcPD9aEOtmPy5Jqt1G3ubY1hQOfWDfHu+UnZZcuXevxQb6ytuuaaa8z26+GPB8O4wLoje3tq5rN91g0+HeMYps94uz8YF++c+vGPf2Q+zhpeB4e68Zx02xurL+pyXqHdMP5QP7xYWrp0mXd+op4wmBBnfyMJo1BsC9urvhJQAkrgchDQNUCNOuFQCwMBc3P0QAwaOFi2bdsWFYpZuCw7Xt0hmZlZcvzYcT8fMnDePNcJlJa2kwP7D/i6snOy5YsvznphyjLRfPfGGP5fypTJU+Xtd96W9997n0mez/q5+SKETMCVc8OQR1yLFi3M+o8LXnbopBwi3DKYZs//ZxxlzdtweeON1yUrK0u2bt0q//kHP5D//j/+VXJycs3amBNeObZuNz8FGG/L4hjxl7oGCHrMBzLN2qwx8vwLz8u3v32r7N2zV8wDpGzdskV2vb3bX9s1Z/ZsOXvunGzZslmuvWattDb986s7fiXDh42QN958Xc6eDfcjdJKBGYGQCeMnyubNm+S8WVtTVFRszpM2sm/fPoj5cl7A/DEGnXTu3EWwfoX1eOrJJ+WDvXv8ekA2GhM7jX2zaNECefyJJ+TC+fNI9hzqV1HRX/bt3SdnvjgjK5avlEOHD0tZx47y1ManpE+fPmb9zFMUD/RRh3bt2svhw4fEbA3uydz3+9/LqpWr5Kc//5mc/jy89skY+qZNWGM0WI4e/Uw6diyTjU9vlF273pKLFy8G6kYkGVKAbWa7GO/6XAO0fPlyefSRR8VMRzTrX05IRuvW8otf/kJ69+oj773/npw5HV6zh/43m1uYc3RLRP//27/9QgYOGChvmnU6Z8/U9K1bHsLDhg+TNhlt5KVtL8oPvv+3nsjP/9//EzM1Vnbs2OGF2R4zYmyuAftlpeF0wtTr0yNHpHOnTvL4hvXSq1dv2bxpsyePP3bdbrn5a/LJJx9LQUGBd965dVu+Ypn88Y9/lJYtW8nMGTMlI6O10dtZ7rrnbjGjlGad0fqkrwFK9Jz6L//lH+R/3nab6eOa9UrgE+u3+K7pM6yvY18kel6Ru/kwsWx99lk5f/6cLJi/UDq0by9/eOiPgWzmL5gv69c/5vUD8/udogdKQAkogUYkoAZQI8LWolKDgNmtylQkJN27l8vuXbtSo1Jai4QJtG3bVk59flK6dO4q7777rp+vtLREPjOGwNQp08xD1no/Xg+UgBJQAkpACSgBJWATUAPIpqHHaUvguuuvkzNnzsimTZu8t+VoqL6BbJrdjbfZIfMPbsb0mbJu3ToxWy/LJjMadPbsGTPKMynuKEvTbLnWWgkoASWgBJSAEmgIAmoANQRF1ZHyBMz6Adm9Ozza07dvP29rXExTUtf0CMAAMutQZO/evRGVx/bZmAaGaWHxpplFZNSAElACSkAJKAElcEURUAPoiuruK7exrgH02quvXbkw0qDl5T17eAbQ1UuWypEjn5pvv3SXu++5K/DbQGnQXG2CElACSkAJKAEl0IAE1ABqQJiqSgkoASWgBJSAElACSkAJKIHUJqAGUGr3j9ZOCSgBJaAElIASUAJKQAkogQYk8P8BrO12cWjuECMAAAAASUVORK5CYII= />"
Question 4
In the first step of the reaction, an alkene is formed. Referring to the mechanism you wrote in your discussion, draw the structure of the alkene and provide its melting and boiling points. Is it relevant to the success of this solvent-free reaction that the alkene is a liquid at room temperature? Explain.
Question 5
Is the product you obtained in this experiment chiral? If so, draw both enantiomers and label all stereocenters as R or S.
Question 6
Below are three molecules commonly found in many types of beef. Explain which of these three would contribute least to the heating of beef in a microwave oven.
Question 7
JSrRwHgRAwJsIDB06hNQYV/TN19+QHoV2bxoL9BUE9E4AAoneRxj2gQAIgIAHCbB4wPNuly5Z5sFeuLdpv1IlRYyZqlWr0uFDR5xuTA0URydOnCBfX1+6euWaqbwUXhCDxIQEGyAAAgYkwPGV1FVRKDS0WapEaAMig8kgAAJpIACBJA3wUBQEQAAEQCB5AkYQSEKbhdKePbtFwL3bt+6IIH3JU/m/sxzgrEjRwsSB/ho1akzbv9tuOgmBxIQCGyAAAgYlwJ5xrdu0JnX1GuKpNXqKX2XQIYXZIKB5AhBIND9E6CAIgAAIeC8BIwgkEdMjaNKkiWKQvtzwpVjRydER27RpI3Xs1FFknzRpMo0dM9ZUFAKJCQU2QAAEDEqAV0hr/3J7GjJ4CM2cOcugFGA2CIBAehKAQJKetNEWCIAACBiMgBEEkp9++onKlS8r4n/Ur1eftm/f4VDMEI4XEhoaQt/HfS/y/3j+ApUoUcJ0hUAgMaHABgiAgAEJ8DLo1WtUI14Vj5f1NVKwcwMON0wGAc0QgECimaFAR0AABEBAfwSMIJDwqA0aNJCWLlsqBnDy5Ck0ZnTKy/LOnjObRo16V5Tp368/LViwUGzLfyCQSBL4BAEQMCKBufPm0siRI+jD5R9Rz549jYgANoMACHiAAAQSD0BHkyAAAiBgFAJGEUj++usvatykER0/flwsbT1o4CCaMmWqiEtiPdYcbyQiYhrN+mAW8fx6Xulof/wByp07t0VWCCQWOLADAiBgIAJ37twRy/qWK1uO4uP3U8aMGQ1kPUwFARDwJAEIJJ6kj7ZBAARAQOcEjCKQ8DDeunWLWrZqQadOnRKjWrx4cerwcgeqV68e5cmTh3gJ6Li4OPrq66/oxo0bIk/lypVp29YYKlq0qNg3/wcCiTkNbIMACBiJQL/+femTTz6hvXv3UVBgkJFMh60gAAIeJgCBxMMDgOZBAARAQM8EjCSQ8Dg+fPiQpk6dQosWLxLb9sY2R44c1LtXb5o2LYJ421aCQGKLCo6BAAjoncCxY8cooE5t6tq1K61auVrv5sI+EAABjRGAQKKxAUF3QAAEQEBPBIwmkMixY/fwqM+iKCHhIJ07d4442GDWrFnFdJqAgDoU/mo4FS5cWGa3+QmBxCYWHAQBENAxAZ52GBLSlA4fOSwCs/r4+OjYWpgGAiCgRQIQSLQ4KugTCIAACOiEgFEFEp0MH8wAARAAgXQlEB0dTV26hqueeNNo1Luj0rVtNAYCIAACTAACCa4DEAABEAABtxGAQOI2tKgYBEAABHRFgKcoVq5SSSx7fuL4ScqePbuu7IMxIAAC3kEAAol3jBN6CQIgAAJeSQACiVcOGzoNAiAAAulOIGJ6BE2aNJE2RG+gdu3ap3v7aBAEQAAEmAAEElwHIAACIAACbiMAgcRtaFExCIAACOiGQGJiIvlXrEDBwfXUlb22ieXSdWMcDAEBEPAqAhBIvGq40FkQAAEQ8C4CEEi8a7zQWxAAARDwBIHuPd6gqKgoOnrkGFWsWNETXUCbIAACICAIQCDBhQACIAACIOA2AhBI3IYWFYMACICALgjsP7CfGjZsQAMHDKQ5c+bqwiYYAQIg4L0EIJB479ih5yAAAiCgeQIQSDQ/ROggCIAACHiMwL///kv16gXTlatXxLK+zz//vMf6goZBAARAgAlAIMF1AAIgAAIg4DYCEEjchhYVgwAIgIDXE1izZg29+b+etHjxEurTu4/X2wMDQAAEvJ8ABBLvH0NYAAIgAAKaJQCBRLNDg46BAAiAgEcJ3L9/nypW8qciRYrQDwcOiuV9PdohNA4CIAACKgEIJLgMQAAEQAAE3EYAAonb0KJiEAABEPBqAuPGjaUZM2fQzp27qEH9Bl5tCzoPAiCgHwIQSPQzlrAEBEAABDRHAAKJ5oYEHQIBEAABjxO4fPkyValamdq3b0/r10V6vD/oAAiAAAhIAv8PAAD//8Gzj04AAD8VSURBVO3dB5QUxdbA8YvkLBIkiKjknHMQJYOCASUIoiKioGR8khRJEgUVRSSDBB+LICggSM5RkgQVQRBFgiKCCKjz9S1ez9czO7M7Kzu7M7P/Pgc6VVdX/YozzN6tkMxlbcKGAAIIIIBAEARSpkohzz77rEx47/0g5E6WCCCAAALhKPDwIw/LF1+slINfHZK8efOGYxUoMwIIRKhAMgIkEdqyVAsBBBAIAQECJCHQCBQBAQQQCCGBBQuipGWrltK69RMyY/qMECoZRUEAAQRECJDwrwABBBBAIGgCBEiCRkvGCCCAQFgK/PLLL1KseFG59dYssm/vPkmVKlVY1oNCI4BAZAoQIInMdqVWCCCAQEgIECAJiWagEAgggEBICSxZslgeefQRGT58hPTs0TOkykZhEEAgaQsQIEna7U/tEUAAgaAK3J4zh3Tu1FleffW1oL6HzBFAAAEEwkdAp0Bs2KihbN++TQ4dPCw5c+YMn8JTUgQQiGgBAiQR3bxUDgEEEEhcgd9++00yZMggyZMnT9yC8HYEEEAAgZASOHDggJQrX1aefPJJmTxpSkiVjcIggEDSFSBAknTbnpojgAACCCCAAAIIIJBoAl26vCQT3p8gmzZtlkoVKyVaOXgxAgggYAsQILEl2COAAAIIIIAAAggggECCCZw/f16KFC0shQoWkg0bNsott9ySYO/mRQgggIAvAQIkvlS4hgACCCAQsIBOxKqbrkSwfv0GKV+ufIzPHjp0SEqVLmnS6NwkA/oPcKe382revLnMnTPPfd3fQUx5+XuG6wgggAACoSPwzvh3pEeP7jJ1yjRp27Zt6BSMkiCAQJIUIECSJJudSiOAAALxJ2AHNTTH4sWLy5bNWyVt2rR+XxBTUMPOiwCJXz5uIIAAAhElcP36dTMXya+//mombM2YMWNE1Y/KIIBAeAkQIAmv9qK0CCCAQMgJ2EENu2D/efk/MmTIUPs02p4ASTQSLiCAAAJJWmDFis+lyQNNpFfPXvLGG8OTtAWVRwCBxBUgQJK4/rwdAQQQCHsB7wCJjiHfvHmL36E2BEjCvsmpAAIIIBDvAk2bNZWVK1fIvr37pWDBgvGePxkigAACgQgQIAlEiTQIIIAAAn4F7ABJ5UqV5dDhQ3Lx4kXz5fbL3XskderU0Z4jQBKNhAsIIIBAkhf4+uuvzfxU9es3kMWfLE7yHgAggEDiCBAgSRx33ooAAghEjIAdINF5Q+rWqSfPv9DR1K1nj54yfPiIaPUkQBKNhAsIIIAAApZA7969ZNxb42TJ4iXSsGEjTBBAAIEEFyBAkuDkvBABBBCILAFngERXnmnQsIGsXr1KUqZMKatWrZaqVap6VJgAiQcHJwgggAAC/xO4cOGCWfb3tttukz1f7jWro4GDAAIIJKQAAZKE1OZdCCCAQAQKeAdITp06JWXKlhb9oluoUCHZvm2HpE+f3l3zQAIkNWvUlL59+7qf8Xdw4sRJ6fj8c+a295LB/p7hOgIIIIBA6ApMmjxJOnV6wfRA1J6IbAgggEBCChAgSUht3oUAAghEoIB3gESr+MGkD6Rz506mti/3flmGDh3mrnkgARJ34jgcECCJAxZJEUAAgRAV+Pvvv6VS5Yry3XffmWV/c+bMGaIlpVgIIBCJAgRIIrFVqRMCCCCQgAK+AiT6el2yUZdu1G39+g3uoTaBBEiSJUsmyZMnN8/G9JfL5RL9Mq0bAZKYpLiHAAIIhI/AunVrpW69utKuXTuZPGlK+BSckiKAQNgLECAJ+yakAggggEDiCvgLkPz0009mqM0vv/wid911l+zfd0DSpEkjgQRIdMJXnc8kti2mvA4cOGBN9jfWmgdllfzwww8mq6JFi0rDBg2lW7fukjt37tiy5z4CCCCAQCIJPN7icVm48GPZtGmzVKpYKZFKwWsRQCCpCRAgSWotTn0RQACBeBbwFyDR10yZMiXaqjYxBTViystXsf3lNX36dPfcJPfdd7/Url1brv75pyxbtkx27d4ld9xxh7VKwqdSokQJX9lyDQEEEEAgkQWOHTsmJUoWlzKly8iGDRvllltuSeQS8XoEEEgKAgRIkkIrU0cEEEAgiAKxBTWaPdRMli79zAyZWbFipWTPll1KlS5pSuQ9LCa2vLyr4StAcvz4cZP/lStXZNHCRdKkyQPux3Q4Ttsn28j8+fOlSuUq5ku3+yYHCCCAAAIhJTBgQH8ZPmK4TJ0yTdq2bRtSZaMwCCAQmQIESCKzXakVAgggkGACsQU1Tp8+LcWKF5Xff//dDLWZ/98oqVipgilfMAIkAwe+JkOHDZVate6VVV+siuagPUiqVKlsrp87e14yZ84cLQ0XEEAAAQQSX+DSpUtStFgR0fmmDh08LBkzZkz8QlECBBCIaAECJBHdvFQOAQQQCL5AbAESLYEOeenw3LOmMPXq1ZeVK1eY42AESL755hv5+czPcnuO26VgwYLmPc6/9u7dKxUqljeXCJA4ZThGAAEEQk9g1qxZ8kz7p+WNN4ZLr569Qq+AlAgBBCJKgABJRDUnlUEAAQQSXiCQAImW6pFHH5ElSxZ7FDAYARKPF/g4GTFyhPTv30/y5csnRw5/HdBqOT6y4RICCCCAQAII/PPPP/Lyy72lRcuWUrFCxQR4I69AAIGkLECAJCm3PnVHAAEE4kEg0ADJmTNnTFfpixcvut+a0AGSgwcPSq17a8pvv/0mH0ycJE8//bS7LBwggAACCCCAAAIIJG0BAiRJu/2pPQIIIHDTAoEGSPRFH374oTz9zFPudyZkgGTT5k3yqNWL5fz58zJs2BvSu1dvdzk4QAABBBBAAAEEEECAAAn/BhBAAAEEbkogLgESfdHjLR6XhQs/Nu9MiACJTu435s0xopO36vbeuxPkySefNMf8hQACCCAQXgJbtm6RGTOmy44dO0RXMrt+/bqkTJlSihYtKhUrVpR27Z6SqlWqhlelKC0CCISMAAGSkGkKCoIAAgggEN8CZ8+elTZt28jq1askb9681pfqmVKzRs34fg35IYAAAggEWUCXcO/StYssW7Y01jfdf38dmfj+RLNyWqyJSYAAAgg4BAiQODA4RAABBBCIHIENGzdI8+aPyi+//CIPPfSwNefIB5IlS5bIqSA1QQABBJKIwO7du+WBB5uIBr11q1OnrrRq2UrKly8v2bJlM8vIb968WebOmyurVn1h0mTPnl0+XfKZlCtXzpzzFwIIIBCIAAGSQJRIgwACCCAQVgLz5s2TZzu0l2vXrslrrw2Uvn36SrJkycKqDhQWAQQQQEDk1KlTUqVqZTl9+rSkT59exr/zrjzxxBM+P9N1SGVUVJRZVv7y5csmKP7l7j2SJ08eKBFAAIGABAiQBMREIgQQQACBcBHYvmO73H//fXL16lV5f8JEad++fbgUnXIigAACCHgJPNj0QVm+fJm5OnfOPKtnYHOvFNFPdUl5XVpet4YNG8mSxUuiJ+IKAggg4EOAAIkPFC4hgAACCISvQIOGDcycI1qDdOnSxViRkyd+kEyZMsWYhpsIIIAAAokjsGfPHqlYqYJ5ufYamT5tRsAFeerpdjJ79myTfsf2nVKmTJmAnyUhAggkXQECJEm37ak5AgggEJECZcqWFu1mHci2aeNmyZAhQyBJSYMAAgggkMACvXv3knFvjTNvXbduvVSrWi3gEmzeslnuvbeWSd+tazcZNWp0wM+SEAEEkq4AAZKk2/bUHAEEEEAAAQQQQACBkBWoXr2a6LBJnWD71A8/muV8Ay2sLv+b547c8uuvv0qlipVk06bNgT5KOgQQSMICBEiScONTdQQQQAABBBBAAAEEQlUge45scuHCBalSuYps2LAxzsWsWbOGbN22VW699VY5e+ZcnJ/nAQQQSHoCBEiSXptTYwQQQAABBBBAAAEEQl4gZaoUpowNGjS0luz9NM7lfeDBB+Tzz5eb565f+yvOz/MAAggkPQECJEmvzakxAggggAACCCCAAAIhL0CAJOSbiAIiEHECBEgirkmpEAIIIIAAAggggAAC4S9QoGB++f7776VYsWKyd8++OFeodJlScvDgQcmXL598+83ROD/PAwggkPQECJAkvTanxggggAACCCCAAAIIhLxAo8aN5IsvVkrq1Knlx1M/xWlZ9osXL0ruPLnk6tWrUrduPVm2dFnI15cCIoBA4gsQIEn8NqAECCCAAAIIIIAAAggg4CUwdtxYefnl3ubqrJkfSsuWLb1S+D+dN2+etH2yjUkwcuQo6d6tu//E3EEAAQT+J0CAhH8KCCCAAAIIIIAAAgggEHIC586dk3vy3y1XrlyR0qVLy+ZNWyRVqlSxlvPatWtSrXpV2bt3r6RNm1a+O3pMsmXLFutzJEAAAQQIkPBvAAEEEEAAAQQQQAABBBJd4OjRo3LXXXdJ8uTJ3WV5/fWBMmToEHPe4dkO8t57E9z3/B10795Nxr873tzu36+/vPbaQH9JuY4AAgh4CBAg8eDgBAEEEEAAAQQQQAABBBJS4OTJk9Kvf1+ZO3euRM2PkmbNHnK//q+//pKmzZrKypUrzLUHHnhQxr8zXvLkyeNOYx+cOnVKevbqKQsWRJlLtWrdK58v/1xSpLixXLCdjj0CCCDgT4AAiT8ZriOAAAIIIIAAAggggEDQBP744w8ZPWa0jBo1Uv7++2/p1rWb9O3bTzJkyODxTk3XqnUrWbr0M3M9TZo0Urv2fVKtWjXJmDGj/P7777J582ZZu3aN/PnnnyZN48ZNZO6cuZIuXTqPvDhBAAEEYhIgQBKTDvcQQAABBBBAAAEEEEAgXgX++ecf0UlU+/brI9rrQ3uFjLImUi1QoIDf97hcLpk5c6Y13GawHD9+3G86HaLTu/fLosNxkiVL5jcdNxBAAAFfAgRIfKlwDQEEEEAAAQQQCBGBVKlTmpIUK1ZM9ny5N6BSzZkzR556up1JO3ToMOnd68ZKIAE97COR/kD76adL5NPPPpWdO3fK4cOH5fr162boQuHChaVmjZrS/LHHpFbNWgH9UDpp8iTp1OkFMzeEzhGhW8pUN4ZBNG/e3PrN/zwfpfC8dOjQISlVuqS5+Oqrr8mA/gM8E/yLs5up53MdO8j06dOlR/ceMnz4iH/x9qTxyNZtW6Vnjx6yfcd2KVKkiLw55k2pV69+wJXXITfaU2T7jh3Wv8NDcu3adWvi1pRWXkWlUsWKpmcJQ2oC5iQhAgh4CRAg8QLhFAEEwkvA/kJtl/r6tb/swwTbO8uQGO9PsIryIgQQSBSBxA6QfPnll9Lx+edE97FtdevWM/ND5M+f329S/cH4/vvvk0KFCsmO7TvdE3Lan6WJFSC52XrqyinlK5STI0eOyBjrh/6XXnzJr0FSvOGcZyRz5swmOPZ8x+clZcobAcCkaEKdEUAg9AQIkIRem1AiBBCIg4D9hdp+JDECFM4yJMb77bqzRwCByBRIzACJToz52OOPyeXLl+WWW24RndehbZs2UqpUaTNPhF7fv3+fzLZ6rCxatNA0wO233y6fLvlMypQpE61BNIhQpWpl65n9sviTxdKoUWN3GvuzNDECJPFVz3Xr11m9IeqanjVr1qyVypUqu+uXVA+c84xcvXrVDH0ZOPB1yZ49e1Ilod4IIBDKAtZ4PjYEEEAgbAVSpEzucv5JjIrUq1/PZf9JjPfzTgQQiGwBK3Dg0j+ly5QKuKKzZ882z+hzI0eNDPg5Z0JrCIsrU+aM5jM2e45srmXLljpvRzu2Vg5xpc+QzqQvVLigy/rBOFqat99529yvWbOGyxrO4nHf/ixv2aqFx3V/JwcPHnR//g8aPMhfslivx3c9W7VuaexLlCzusgICsb4/UhNYk6669N9hvrvuNO1k9Rpy7dmzJ1KrS70QQCBCBCRC6kE1EEAgiQrYX6jtfRJloNoIIBDBAokVIKlRo7o7APHJJ4sCEh4xcoT7mXFvjfN45tdff3XlzpPL3F+48GOPe3pif44ndIAkvuv57bffuoNTAwb0j1bPpHBhy9YtrmrVqpo2vSf/3a6oqPnRAmJJwYE6IoBA+AkQIAm/NqPECCDgELC/UNt7xy0OEUAAgYgQSIwAyabNm9wBi2faPx2w48WLF929SLRnnXMbPGSwyTNX7pwu7V3gvdmf4wkZIAlGPbVejzz6iAmSZMyUwfXDDz94VzViz0+cOOFq+2Qb085a9yFDh/jsSRSxAFQMAQTCXoAASdg3IRVAIGkL2F+o7b1qVKxUwXw5u/ueu1zWKgs+gfS63tfnNL297dy103y509942XnemiWzq3LlSq7+/fu5rKUF7aTu/aPNH3XZf9wXrYPHWzxu/rw59k1z2VrS0FW9ejV3viVLlXC99tqrritXrjgf8zjevGWz68l2bV135svrfk67rr/4YmfX119/7ZGWEwQQiEyBxAiQdO3axf2Zs37D+jjBfv/9965jx465rOVb3c/pcJoCBfObPLt0ecl93Xlgf+YmZIAkvutp10eHI9nt1rt3L/tyxO4vXbrkatP2CXdwTI+tSVkjtr5UDAEEIleASVpDeYIYyoYAArEKWF9APdLoJKnWGHfp2bOHub527TqpXq26Rxo9sX5raC0FeK+5rqsNdHmpi1hj2GXYsKFi/WbTXE+TJo1ZXeHPP/90X9PZ9j+a95E8+GBTk0b/cpbBOUmrfb1Jkwckbdo0EhUV5X7GeVC79n2y4vMVHktjWv/tSJ8+r8jYcWNFl53ULW3atGZvBVTMPnny5DJo0GCzfGeyZMnMNf5CAIHIE7Anab3zzjtl4vsTA6rg6tWrZdToUSbtv1nmt1LlimbVmvTp08vPp89I6tSpA3qvv0QbNm4wK9fo/c+Xf24d14mW1P7M1CWD+/btG+2+94UTJ06a1XX0+r9d5je+62mXUZeitebekLNnz5rJSL8/fsJM3Grfj5S9/v9kBf+l98u95MyZM5IvXz6ZMWOmz/93I6XO1AMBBCJbgABJZLcvtUMg4gXsL9R2RTVA8dtvv8kdefOIBjZ0mcU33xxr33bve/ToLu+Mf0c0CPLDyVOyd99eqVu3jvaqkwrlK8jIUaOkUsVK5oeC8+fPy7yPrC+AvXuJ1fPEfNk99t1x9w8MzjL4CpBoUEWf0+Uvu3frJkWKFJVjx76zAiB9ZMfOHaZMs2Z+KC1btnSXT4Mjo8eMNucaQBk2bJiULVPWnK9du0b69+8vu3bvMufvT5go7du3dz/LAQIIRJaAHSD5t7X6NwESa3JW0WBs2bJlZfu2G59T//b9+pw1F4cMHzHcBAk04JIpU6Zo2Tk/S6PdjOXCvw2QxHc9ncVs0bKFWHOtmEu6Yk/Dho2ct4NyvGLF57J8+fKg5K2ZHjx00KxedGfeO+XyH3/I8mXL5MeffpRs2bKJrlbTtGkzmTVzVtDeT8YIIIBA0AUit3MMNUMAgaQgYHfJtvd2na0vpqYrtw6jsX6TZ182ez23h9doOt2ef6Gjuzv57t27zTXvvzp37mQmGNRJBrfv2O6+bb9b987Nef31Qa9HG+6jE/nZaZxdyvft22e6Zuu9uvXq+hyrr92Zi5coZp7PcXt2l05+yIYAApEpYAUO3MM10qZL4wrkT+o0qdzP/JtVbOzPplq1asYLaoOGDcznVeEihfzmZ79T65smbepY/2gd7Wf+7So29vPxVU9n5XTCWrvtdP6VhNg6PPes28SuW7D3+k7rFxNmSKn+/6jDqdgQQACBcBVgDpJwbTnKjQACRsD7i5/NsnTpZ+4viRs3bbQvm/2aNavd9zSdbjpe2s7L1+oKJpGfv+zndO/c7OuNmzR2XvY4tsfkO5fv1PH59rM6J4q/7eOPF7jTTZ482V8yriOAQJgL2D9kOz8nYquSv2V+9QfZvn37uIoULez+/KhatYpZjtX5g639GRRfgQM7KP1g0wf9Ft1+pzNg7DexdSO2ZX6XL1/matS4kUvnkdK8b8+Zw6V5O4Pg9jvjq57O8ur/L3bb2cF45337+K233zLle+GF5+1LHvuvvvrKlFvLb9ej/bPP+JwTS9vw8uXLQfvTocONAMzRo0fNO5xLOU/8YKIp3969ez3KzwkCCCAQTgIESMKptSgrAghEE7C/3Np7O4FOwmoNszFf1p7t0N6+bPZ6run1vqbT7YNJH5hrel1/c9nkgSYu/bIXyBc9+926d2729Zi+7OsPPJrO+YNPufJlzbX8Be5xZhft+Pfff3fpKgH6fFxWmYiWERcQQCCkBewfsp2fE7EV2FeARIMjZcuVMZ8ZurStrjCiy9AWLVbEXNOeAPZmf37qpNDxsdmfh/qDvb/NThPTZ6bz2ZgCJAMHvmbqlDXbbS7t/ae9OTQQrp/vmW/N5Fq16guTVXzX01k+DcTYbVelSmXnLfexNTeLK1v2rKasvgIkel/Law2zcmmQxVmPLLfd6jp8+LA7r4Q40OV6tZ0+/PDDaK+ze0Vaw0Oj3eMCAgggEC4CBEjCpaUoJwII+BSwv1Dbe2ciax4P80VOv3zagRDd219G9b69WfOVuJo/1tykt/Oy9zlz3W5+ezd16lSXBiW8Nzud7p2bfT2mL/u+AiT6hVqf1S/E6TOki/GP/Q5dZYcNAQQiU8D+IftmAyQ61E8/M3SFLecyuxo4yXvnHeaH+V27dhnE++vcb9KmS5/W9csvv9w0rP1ZlRABEh2mqJ+fupyw9xK7M2fONPXS3ntqEN/1dEL5C5BMmTLFBKc0EG+76N47QKL/L2mgXO9NmjTJmbXL7nUSU88Ujwfi6eTcuXOmPE8/81S0HLX3ipa3YaOG0e5xAQEEEAgXAQIk4dJSlBMBBHwKOL9c6rFz02Vw7fu65KJuurev+Vom15rgzvXU0+1cOq+Hnc65199GWpO7Ol/jkc55w34urgES+znd6xj7QP74++2kszwcI4BAeArEV4BEl7TVgMDWbVujQWgvNP3MGfPmGHNP5y2xP4vmzJkTLX1MF1566UWXBkJ0GXN7s/NKiABJr149Tdl1aXbvTYMi9ue79niI73o63+cvQKIWOo+MBhO0R6O9rLx3gER7aWja8hXKeQS09B0atNLl3hNjCWFr5R+z9LxzSJZd7+c6djBB/ZiWr7fTskcAAQRCUYAASSi2CmVCAIGABewv3fbe+8H77qttvmDaX8p1r2n1ekybTuS6bfs21/h3x5vhNrdlzWKes99jLWvofty+pnvnZl+Pa4AkQ8b0AZXR+S6OEUAgcgXiK0ASk9CjzR81nzszZswwyb7//nsTnNXPMf2B+OrVqzE97r6nPVDszz7n0L+EnINEh53o0JSffvrJXS7ngT2XhwZI4ruezvf4m4NEe2FcuHDBnVR7AKqZd4BEg/V63Vr9x502FA7s3pk6xMl7++ijj0yZv/hipfctzhFAAIGwECBAEhbNRCERQMCfgP1F3N57p9NuyXpPh9XoxHX28Brv7srez3mfX7x40WV3T9f8Hnr4IXcS+926d2729bgGSHTCRH1WyxroDyXO93KMAAKRJRDsAMnmLZvNb/3vujufxzDCbt26ms8i/TzSuUpi27RHwWOPP+Z+xp4EW5+zV7EpVbqk32wC+cx0PhzTHCTOdM7jPXv2mKFEOnGrDmHRLT7r6XzX2++87Z6DxFdvFjutvwCJPQRz/Yb1ZqiQ9nbRHif/+c/LrnXr19mPJ/he52/RtvLuTakFOXv2rLmnZWRDAAEEwlGAAEk4thplRgABt4D9hdreu2/870ADG3bvD3t1GD3X687tkUcfMV/gnb/xdN7XYw2w2O+pWbOG+7Z9TffOzb4e1wCJLgdpP/vpp0ucWXocb9q8yZRZf/D47LNPPe5xggACkSMQjACJBgeebNfWDLnRYXw6TM+ef8SW0zmX7Eld9TNJh0/oD8C+tvPnz7t0Xgr7s8t7HgodCqL3dJJUnfPE12Y/G9NnpvO5uAZIdA6qOnXrmHI4Az7xWU9n+XSuF7vt7GGezvv2sb8Aid2bUIcq6XxUOilrseJF3cbaw8SeX8vOKyH2OnxGy+P8RYHzvRUqljfDgpzXOEYAAQTCRYAASbi0FOVEAAGfAvYXanvvK5E9tt5O4ysIYn9p1on9jhw54isbl85PYufh7AptX9O9c7Ovx/Rl3/4NoXPyxWPHjrmDOgULFXD9+OOPzmzNsY6jt7vE6w83hw4dipaGCwggEBkC9g/Zzs+J2GrmaxUb5zO6PKvmpyvYaP76w7fOaXHt2jVnMhMQsXu16Wea9rxo1bql643hb5geBDr844k2rV06P5P9madzZngPb9FeEPZ9ewUZjxdZJ/b9mD4znc/EJUCiASH9gV7f0fqJVkGrp10+DVzkzpPL2Oo+pkCGvwCJ7aHP67Lu9sS6OvGsBrT0vq7Qkxhb/Qb1zb8FX/XS3iNatp9//jkxisY7EUAAgZsSIEByU3w8jAACiS1gf4G0977KY3cHttP4+nL+ySeLzBdZTZPvrjvNCgFffvml6/jx464DBw6Yifzsif30BwRnQMLOV/fOzb4e05d9XwESzUNXWtAfWjQP7fauXbX3799vyjN//nwzh4qdf2J9QXbWlWMEEAieQDACJM7Snj592vXwIw+bzxtfn1caNNGlW3VFL/tzx9del6PV5XXtoSvOd+hwQXsyUu3N52uz8/RVBl/pAw2QaEDBDvJoLxgNDvna4qOedr7aY8Rut9gmUo0tQKJzpXhvGki3J/DW3jsJvelyw9peOjzLe7N/mTB37lzvW5wjgAACIS+QTEsobAgggECYClhfQD1Kfv3aXx7n9knxEsXEWrVGChUqJF8dOGhf9thPnz5dunbrItaXZ4/rzpOcOXPKggUfS6WKldyXnWVwvt++3rx5c5k7Z547vfOgTNnS8tVXX0nx4sVlz5d7nbfE+nIp3bp3FWu1Ao/r9kny5Mmlw7MdZPToMZI6dWr7MnsEEEAgzgLWpKFiBTDk0qVLsn/fASlcuHC0PKwgh6xbt1Z27NwpR44clmvXrps0RYsUkSpVqkjNmrUkXbp00Z6zLwwZOkRef32gZM+eXX44eUpuueUW+1bQ9tZcHdKyZQvzOdqrZy8ZMmSoJEuWLMb33Ww9NXOrh58sWbJY0qRJI4cOHpY8efL4fafVG0R27d5lPs/fe2+CO132HNlE2+XkiR9E/+/x3ipXqSTWSjmyZPESadiwkfftoJ7re/X9r702UPr36+/xLmsIjlhzaFnuLWXK5Kke9zhBAAEEQl2AAEmotxDlQwCBGAWioqI87mswwtdWp879YnXxloEDX5d+ffv5SmKuWb+JkxkzZ8iOHdutHwCOiNWl2VwvVqyY1K/XQFq1amW+8DozcJbB+f5BgweZZMWtZx991He53p/4vpw5c0Zy5Mghz3d83pmtObbGxsusD2fJpk0bxerJYq7lzp1HKpQvL+3aPSUFChSI9gwXEEAAgX8jYA01lPVWQGFB1AJp2rTZv8kixmf0h31raVux5oCS+f+dLw899HCM6W/25oT3J4g1AatkzJhRJr4/0e/n8M2+x/v5o0ePijV0yVx+5T+vyKBBg72TeJz7C5BUr15Ntlv/Fy1bukzq1q3n8YyeBLu9or3QccGakFesHkVSongJWb16jePOjcN69etZv5Q4IsePfR9rQCraw1xAAAEEElGAAEki4vNqBBBIGIEdO3eIftHUHhfffnM0xt/kJUyJeAsCCCCQ8AKFixQyPUR27tgluXLlilYAu6fdmjVrpUb1GtHux8cFa6iOWMvEStUqVa3eKOuD9sPzqNGjpF+/vpItWzb5dMlnUq5cufgofkB5WHOciAbOtRfOpo2bJVOmTDE+5y9Aok7q1emFTvLWW2975GHN/WGCTdZcL3L40BHJnz+/x/2EOGnZqqVYw1Pl7JlzkiFDBo9XWnPTiDURruzds0/0FwxsCCCAQNgIhPwgIAqIAAII3ISArjyjK87oWGmdWJANAQQQSKoC9hK8Ok+I9xYVNd/MmaHzhOgqJcHadC4Se2Uc5zLA8fm+1atXmbroimXWEMb4zDrWvNauW2venTZdGtfWbVtjTa8J/M1BcuLECZeuZJMpc0bXvn37PPKaPHmy+X/t3ntreVxPyJMPJn1gyuCrHa2eL+beW2+/lZBF4l0IIIDATQvQgyRsQlkUFAEE4iLwzvh3RH/DNmfObNm7d6+kSJFCNm7cJOXLlY9LNqRFAAEEIkbgm2++kfvury3W6iLWEL12UrdOPWv4SQZZs2aNvPveu5IqVSr52JpjqU6dukGtsw4buf/++8ycUDu27zS9++LzhZr3ho0bzBwnOgeIv03nfbr77rv93Y7zdWuSV7FW8DHDM8eMeVNeevGlgPLw14NEH7aCEPLSSy9K5syZ5ZVX+khhax4tZ3tpD5USJUoE9J74TmRNFCuFCheUrl26mrmwnPnr8NTbc+aQqlWrmTlSnPc4RgABBEJZgABJKLcOZUMAgX8tUKRoYdFx4PY2dOgwebn3y/YpewQQQCBJCpw6dUr69usjixYtck9InTJlSmnQoKEM6D8gwYaiTJo8STp1esHnJJ832zA6+bX1K8RYs9GhN3nz5o01XaAJrBVyZLo12XeP7j1k+PARgT4mVu9GsVZGM3OkaBt4bwsXfix9+vbx+D+tZo2aMn78u4k+fEUDJOnTp5cvd+/xLrZYPZbEWtHGDMHR4BsbAgggEA4CBEjCoZUoIwIIxFngqafbibVMr9yW5TbpaE1+qrPpsyGAAAII3BDQSTYPHz5sTu65555ok0/jFHoC1pAbM4eMroijPUpCYXuh0/NiDffxudKOTkKuvV+++GKV3Fvr3lAoLmVAAAEEYhUgQBIrEQkQQAABBBBAAAEEEEDAW0Ano9UeMDNnzDKrvDnv65CuYsWLiq7kM3jwEOctjhFAAIGQFSBAErJNQ8EQQAABBBBAAAEEEAhdgfPnz5vlfnVOm8mTpngUVIc56bLOt+e4XbZs2epxjxMEEEAgVAUIkIRqy1AuBBBAAAEEEEAAAQRCXKBylUpm4t9j3x2Ptmyzzssybdo0Of3Tz5I1a9YQrwnFQwABBEQIkPCvAAEEEEAAAQQQQAABBP6VQF9rAtlRo0fJgf1fSeHChT3y+Oijj6RN2ydk7px50rx5c497nCCAAAKhKECAJBRbhTIhgAACCCCAAAIIIBAGAqtWfSENGzWUt956Wzq90MmjxGfOnJE8d+SWZ555Ria+/4HHPU4QQACBUBQgQBKKrUKZEEAAAQQQQAABBBAIA4ErV65ItuxZpWHDRrIgakG0EpevUE4uXLgg335zNNoQnGiJuYAAAggksgABkkRuAF6PAAIIIIAAAggggEA4C9RvUF927dopP58+IylSpPCoysQPJsqc2bNl9eo1kjx5co97nCCAAAKhJkCAJNRahPIggAACCCCAAAIIIBBGAiNHjZR+/frKxo2bpHKlymFUcoqKAAIIeAoQIPH04AwBBBBAAAEEEEAAAQTiIHDq1Cnp26+PDH9jhOTKlSsOT5IUAQQQCC0BAiSh1R6UBgEEEEAAAQQQQAABBBBAAAEEEkGAAEkioPNKBBBAAAEEEEAAAQQQQAABBBAILQECJKHVHpQGAQQQQAABBBBAAIGwFfj7779l7ty5ErUgSvbt2ysnT540dcmbN6+UKlVamj/aXFq1asWErWHbwhQcgcgWIEAS2e1L7RBAAAEEEEAAAQQQSBCBrdu2yvPPd5SvvvoqxvcVKFBApk2bLlUqV4kxHTcRQACBhBYgQJLQ4rwPAQQQQAABBBBAAIEIE1i69DN5vMXjcvXqVUmdOrU88/Qz0rBhQylbtpwkS5ZMDhzYL4sXL5ap06a60/z3o/9K48ZNIkyC6iCAQDgLECAJ59aj7AgggAACCCCAAAIIJLLAoUOHpGq1KnL58mUpVKiQfDhrthUYKeuzVAcOHJCWrVrIkSNHTCBl65ZtUqJECZ9puYgAAggktAABkoQW530IIIAAAggggAACCESIgMvlklq1aooOr8mQIYNowKNw4cIx1u748eNStlwZuXTpkhlms379BtPLJMaHuIkAAggkgAABkgRA5hUIIIAAAggggAACCESiwKbNm6R27XtN1UaNGi3dunYLqJrj3honvXv3MmnXrl0n1atVD+g5EiGAAALBFCBAEkxd8kYAAQQQQAABBBBAIIIFunR5SSa8P0FSpUolx499L9mzZw+otmfPnpW77s4n165dkxeef0HefvudgJ4jEQIIIBBMAQIkwdQlbwQQQAABBBBAAAEEIligSpXKsmv3Lilfrrxs3botTjW9mWfj9CISI4AAAgEKECAJEIpkCCCAAAIIIIAAAggg4CmQLXtW+e2336Rt27Yydco0z5uxnD3T/mmZNWuWZM6cWc6dPR9Lam4jgAACwRcgQBJ8Y96AAAIIIIAAAggggEBECqRMlcLU68XOL8rYsePiVMfu3bvJ+HfHm2euX/srTs+SGAEEEAiGAAGSYKiSJwIIIIAAAggggAACSUCAAEkSaGSqiEASEiBAkoQam6oigAACCCCAAAIIIBCfAvfkv1tOnjwpzZo9JFHzo+KUdfPHmssnnyySvHnzyndHj8XpWRIjgAACwRAgQBIMVfJEAAEEEEAAAQQQQCAJCNSrX0/Wrl0j+fPnl0MHD0uyZMkCqrXL5ZKixYrI0aNHrWWC75OVK1YG9ByJEEAAgWAKECAJpi55I4AAAggggAACCCAQwQJvDH9DXn11gKnhl7v3SIkSJQKq7YEDB6RsuTIm7aBBg6XPK30Ceo5ECCCAQDAFCJAEU5e8EUAAAQQQQAABBBCIYAEdXlO4SCG5fv26PPHEEzJ92oyAavvU0+1k9uzZkjJlSjly+GszzCagB0mEAAIIBFGAAEkQcckaAQQQQAABBBBAAIFIF3jxxc4y8YOJppozps+U1q1bx1jlqKgoadW6pUnT8bmOMn78uzGm5yYCCCCQUAIESBJKmvcggAACCCCAAAIIIBCBAleuXJHqNarJ/v37TY+QV6zhMjpkRnuHODftZTLmzTEyePAguXbtmhQtWlQ2b9oiGTJkcCbjGAEEEEg0AQIkiUbPixFAAAEEEEAAAQQQiAyB06dPS+MmjUyQRGuUO3duadSokTUnSUlTwQMH9suyZcvkxx9/NOclS5aUpZ8tk5w5c5pz/kIAAQRCQYAASSi0AmVAAAEEEEAAAQQQQCDMBf744w8ZOXKEjB03VvTY15YuXTrp3Kmz9O8/QPSYDQEEEAglAQIkodQalAUBBBBAAAEEEEAAgTAXOH/+vOktsm/fXjlhTeKq251580qpUqVNr5KsWbOGeQ0pPgIIRKoAAZJIbVnqhQACCCCAAAIIIIAAAggggAACAQsQIAmYioQIIIAAAggggAACCCCAAAIIIBCpAgRIIrVlqRcCCCCAAAIIIIAAAggggAACCAQsQIAkYCoSIoAAAggggAACCCCAAAIIIIBApAoQIInUlqVeCCCAAAIIIIAAAggggAACCCAQsAABkoCpSIgAAggggAACCCCAAAIIIIAAApEqQIAkUluWeiGAAAIIIIAAAggggAACCCCAQMACBEgCpiIhAggggAACCCCAAAIIIIAAAghEqgABkkhtWeqFAAIIIIAAAggggAACCCCAAAIBCxAgCZiKhAgggAACCCCAAAIIIIAAAgggEKkCBEgitWWpFwIIIIAAAggggAACCCCAAAIIBCxAgCRgKhIigAACCCCAAAIIIIAAAggggECkChAgidSWpV4IIIAAAggggAACCCCAAAIIIBCwAAGSgKlIiAACCCCAAAIIIIAAAggggAACkSpAgCRSW5Z6IYAAAggggAACCCCAAAIIIIBAwAIESAKmIiECCCCAAAIIIIAAAggggAACCESqAAGSSG1Z6oUAAggggAACCCCAAAIIIIAAAgELECAJmIqECCCAAAIIIIAAAggggAACCCAQqQIESCK1ZakXAggggAACCCCAAAIIIIAAAggELECAJGAqEiKAAAIIIIAAAggggAACCCCAQKQKECCJ1JalXggggAACCCCAAAIIIIAAAgggELAAAZKAqUiIAAIIIIAAAggggAACCCCAAAKRKkCAJFJblnohgAACCCCAAAIIIIAAAggggEDAAgRIAqYiIQIIIIAAAggggAACCCCAAAIIRKoAAZJIbVnqhQACCCCAAAIIIBAngZSpUnikv37tL4/zpHCCQVJoZeqIAAL+BAiQ+JPhOgIIIIAAAggggECSEiA4IIJBkvonT2URQMBLgACJFwinCCCAAAIIIIAAAuEpcPDgQSldppQp/IABr8qr1p+4bPUb1PdIvuLzFR7ncT3Jlj2r/Pbbb+axc2fPS+bMmeOaRYKnj2+DBK8AL0QAAQRuQoAAyU3g8SgCCCCAAAIIIIBA6AjcbIAkvmsSjgGS+DYgPwQQQCCcBAiQhFNrUVYEEEAAAQQQQAABvwIESPzScAMBBBBAIAABAiQBIJEEAQQQQAABBBBAILQF3hn/jvx8+rSMGDnCFLRBg4bSoEEDyXpbVmndurW0aNnCXYGP5n0k33zzjbw+aKAsX77cDIN5rsNz8vOZM+40ehA1P8p9vmv3LnnrrXGyadMmOXHihLmeIUMGKVyosNSrV0+efbaD5MuXz1zXsujWr19fuXLlijkeOnSYpE2bVvLfc480btzEXNO/tmzdIu+/P0HWrl0rP/74o7l+j5Wmfr360qVLVylYsKA7rfPg/Pnz8sGkD2TVqlWyb99e+fXXX83tLFmySJHCRaRR48aidcqaNav7sZsxsJ/Nettt8t57E2T//v3y5tgxxu/cuXOSKlUqqVihorRs1Uo6PtdRkiVL5n4vBwgggEC4CBAgCZeWopwIIIAAAggggAACfgW8Jxe1ExYrVkz27tnnMfnoyhUr5bHHH5MLFy7YyaRdu3YyY8YM97ke2KvYDBo8SIYNGyp///23uZ8mTRpJnjy5/Pnnn+5rKVOmFA28PPhgU493eWRonTRt2kwWRC0Ql8slffq8ImPHjZV//vnHJNMAim52UEXfMWjQYOndq7dHwGH9hvXSosXjooEJ3W655RYTfNFjfdbOL1u2bLJo0SdSuVJlveVRrrga2L558+Y1gZu+ffvI9evXTb7ef2lAavq0GR5l9k7DOQIIIBCKAgRIQrFVKBMCCCCAAAIIIIBAnAQGDnxNzp49a3pV6IO1ataSmjVrSvYcOaRzp84ewQENZuifZs2aSbly5c178uTOI62faOXxTg2QaDCibt06JqBRoXwFGTlqlFSqWElSp04t2otj3kfzpHfvXiZYkD17djn23XF5441hJp/RY0bL1atXzXGvnr3MM0WKFJWWLVua4Ije16127fusAMwwKVumrDlfu3aN9O/fX7TXim7vT5go7du3N8eXLl2SYsWLyk8//WQCI/37D5D2z7SX3Llzm/vaC2XK1CkyZMhgEyjRMm/ZstXcs4McehIXA5P+f0sga9BGgzs5c+aUV17pY5zTp08vq1evlv+88rI76PSJFZhx9pQxBeAvBBBAIMQFCJCEeANRPAQQQAABBBBAAIHABGKag8QZHChZsqQ1fGaB6FAW5+ZMo9c1QPJCp+dl8uTJJtn2bTukbNkbQQzncy++2FkWLlpoLmmPDR1qopu/SVp1eEr5CuVMoEGDI58v/9wEO8xD//vr8uXLUrlKJTly5IjcZg1rOXL4a7n11ltl4cKP5XGr94huPbr3kBEjRv7vCc9ds4eaydKln5leHN98/a0Z/uOsX1wMNGfns/ffX0fmzplryuV8qzqpl25t2rSRaVOnm2P+QgABBMJFgABJuLQU5UQAAQQQQAABBBCIUSDQAMmpH36UHFbPEu/NGQTQexogaftkG5k3b55JOv+/8+Whhx72fszvub8ASdeuXeS9Ce+Z57Zu3Sbl/9eLxTsjZzDE7kWyZ88e2bFzh0lar249ueuuu7wfM+c6LGiw9Ue3RQsXSZMmD3gEOeJioHnYNur23dFjpjeMXndup06dkrvuvjEPS+nSpWXnjhs9YJxpOEYAAQRCWYAASSi3DmVDAAEEEEAAAQQQCFgg0ACJPbeId8Z2EMC+rukmTZ4knTq9YC6lSJFC6tSpa80j0lSqVK4ipUqVspP63PsLkGjvkX379pleHd9+c9Tns3pRh9PkzpPLzCvy5JNPypTJU32m/f333818JIcOHXTf16E/c+fONee+AiRxMdBMbBudg0QDJL42ndMle45s5hYBEl9CXEMAgVAXIEAS6i1E+RBAAAEEEEAAAQQCEghGgETnEGnTto012emNITTOgugkqLVr17ZWnGkgjz32mOiqNs7NX4AkVeqUZniNTq6qc4HEtNlzmGgvE+1tYm8HDhyQadOmyucrPpejR4/KX3/9Zd+KtidAEo2ECwgggIBPAQIkPlm4iAACCCCAAAIIIBBuAsEIkNgGK1eukDlz51jzeiyVX375xb7s3mfOnFkGDnxdXuz8ovuavwCJ3RtDE+qkp4FsOoGrPdmqDp/RiWDtoEiJEiWkTJkycvfd/z+nyvr162XdurUmawIkgQiTBgEEEBAhQMK/AgQQQAABBBBAAIGIEAhmgMQG0qV+dXWZHTt2yLJly6ygxWa5ePGifVs+nDXbWoK3hTn3FyDJmCmDWSK4Zo2a1uova9zPBnLgnAhVh/jMmD5TNEDivcU2BwlDbLzFOEcAAQQIkPBvAAEEEEAAAQQQQCBCBBIiQOJNpfN/jB031j0h6gMPPCgLP74xHMdfgKRatapmolVdlUYnS02VKpV3tn7PS5YqIYcPH5aMGTPK4UNHfE42qw8TIPFLyA0EEEDArwA9SPzScAMBBBBAAAEEEEAgnASCESB5tPmjokvu5smT2+8kqX/88YdkvjWToapapaqsX7/BHPsLkAwZOkRef32gSWMPfzEnXn9ttnqnDBp0YyWaLi+9JI0bN3FPllquXDnZtnW71xP/fzpw4GsydNhQc8F+h3NoDz1I/t+KIwQQQMAWIEBiS7BHAAEEEEAAAQQQCGsBZ4CkV89e1jwdw931+bfBgbr16pq5PHRC1f37DkihQoXcedoHOj9J4yaNzWmHZzvIe+9NMMfOAMn3x09I7ty5zfXjx4+LrmSjQ3PuvvtuWbd2veTKlcvOzuz/+ecfebzF4/LJJ4vMPCV7vtwrRYoUkZy5bpfz589LpkyZ5Mjhr0UnivXetDwtWrYQ7d2iGwESbyHOEUAAAd8CBEh8u3AVAQQQQAABBBBAIMwEnD057rnnHmuoyyITSMiSJYvcmiWzuzZx6T2xePEn0vyx5mbVmTx58kiPHj2lVs1aonnqMrxLly2V0aNHmYlbdRWbLZu3mkCGvqxq1Sqyc9dO897OnTpLr1695fr166JL5eoSvO2ffcbke8cdd5h876t9nxk6o/ObvPfeu7Jh442eKB2f6yjjx79r8unXr6+MHDXSHJcsWVL69uknFStWNOf63MJFH8v8+fNNvuai9RcBEluCPQIIIBCzAAGSmH24iwACCCCAAAIIIBBGAg82fVCWL1/mUeK9e/ZJ6TKl3NfiEiDRh6ZPny5du3URDcD423LmzCkLFnwslSpWcid51wpydOvW1X1uH5w7e1501RsNknTr3tXnqjiaVle40R4po0ePkdSpU5vH//zzT3mizROigRt/W/Vq1SV/gfwyc+ZMk4QAiT8priOAAAKeAgRIPD04QwABBBBAAAEEEAhjgQsXLpgJU7X3xdWrVyVTxkxWIGKeTJ021V2rVwe86j52HkRFRTlPpXnz5u5zHdYyY+YMa/Wa7XLkyBHR1Wx0K1asmNSv10BatWoladKkcafXA5fLJbNnz5a58+bKDz+cNPeyZcsuSxYvkXTp0plzHQYz68NZsmnTRjlw4IC5ljt3HqlQvry0a/eUFChQwFxz/qX5rljxuUQtiDKr6eh59uw5pLS1qs1DDz8sNarXsOZBWSdr1641j7Vq1doMDdKJW+0trgb2sxrY6doletBH89Xgjd27RQNGz3V4zn4dewQQQCAsBAiQhEUzUUgEEEAAAQQQQAABBBBAAAEEEAimAAGSYOqSNwIIIIAAAggggAACCCCAAAIIhIUAAZKwaCYKiQACCCCAAAIIIIAAAggggAACwRQgQBJMXfJGAAEEEEAAAQQQQAABBBBAAIGwECBAEhbNRCERQAABBBBAAAEEEEAAAQQQQCCYAgRIgqlL3ggggAACCCCAAAIIIIAAAgggEBYCBEjCopkoJAIIIIAAAggggAACCCCAAAIIBFOAAEkwdckbAQQQQAABBBBAAAEEEEAAAQTCQoAASVg0E4VEAAEEEEAAAQQQQAABBBBAAIFgChAgCaYueSOAAAIIIIAAAggggAACCCCAQFgIECAJi2aikAgggAACCCCAAAIIIIAAAgggEEwBAiTB1CVvBBBAAAEEEEAAAQQQQAABBBAICwECJGHRTBQSAQQQQAABBBBAAAEEEEAAAQSCKUCAJJi65I0AAggggAACCCCAAAIIIIAAAmEhQIAkLJqJQiKAAAIIIIAAAggggAACCCCAQDAFCJAEU5e8EUAAAQQQQAABBBBAAAEEEEAgLAQIkIRFM1FIBBBAAAEEEEAAAQQQQAABBBAIpgABkmDqkjcCCCCAAAIIIIAAAggggAACCISFAAGSsGgmCokAAggggAACCCCAAAIIIIAAAsEUIEASTF3yRgABBBBAAAEEEEAAAQQQQACBsBAgQBIWzUQhEUAAAQQQQAABBBBAAAEEEEAgmAIESIKpS94IIIAAAggggAACCCCAAAIIIBAWAgRIwqKZKCQCCCCAAAIIIIAAAggggAACCARTgABJMHXJGwEEEEAAAQQQQAABBBBAAAEEwkKAAElYNBOFRAABBBBAAAEEEEAAAQQQQACBYAoQIAmmLnkjgAACCCCAAAIIIIAAAggggEBYCBAgCYtmopAIIIAAAggggAACCCCAAAIIIBBMAQIkwdQlbwQQQAABBBBAAAEEEEAAAQQQCAsBAiRh0UwUEgEEEEAAAQQQQAABBBBAAAEEgilAgCSYuuSNAAIIIIAAAggggAACCCCAAAJhIUCAJCyaiUIigAACCCCAAAIIIIAAAggggEAwBQiQBFOXvBFAAAEEEEAAAQQQQAABBBBAICwECJCERTNRSAQQQAABBBBAAAEEEEAAAQQQCKYAAZJg6pI3AggggAACCCCAAAIIIIAAAgiEhQABkrBoJgqJAAIIIIAAAggggAACCCCAAALBFCBAEkxd8kYAAQQQQAABBBBAAAEEEEAAgbAQIEASFs1EIRFAAAEEEEAAAQQQQAABBBBAIJgCBEiCqUveCCCAAAIIIIAAAggggAACCCAQFgIESMKimSgkAggggAACCCCAAAIIIIAAAggEU4AASTB1yRsBBBBAAAEEEEAAAQQQQAABBMJCgABJWDQThUQAAQQQQAABBBBAAAEEEEAAgWAKECAJpi55I4AAAggggAACCCCAAAIIIIBAWAgQIAmLZqKQCCCAAAIIIIAAAggggAACCCAQTAECJMHUJW8EEEAAAQQQQAABBBBAAAEEEAgLgf8Dim9L6OPBsKYAAAAASUVORK5CYII= />"
Question 8
In each of the following lists, which compound would you expect to heat most rapidly in a microwave oven? Explain.