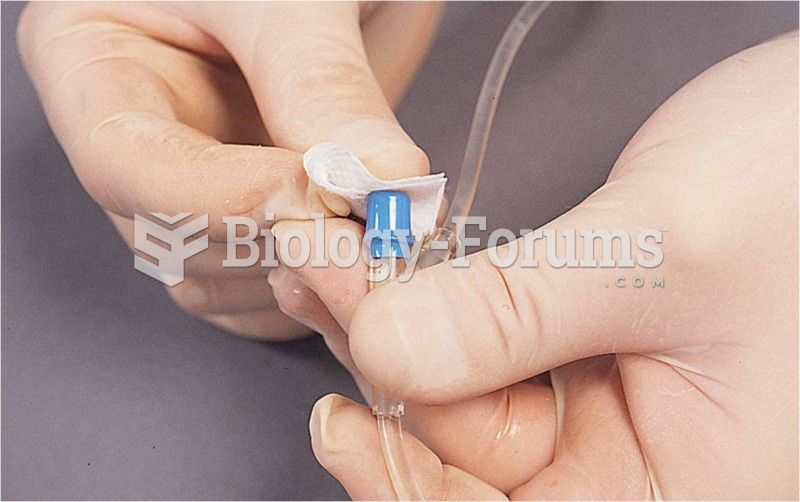
You and one of your peers might have observed the following situation in Part I of this experiment. Student As sample melted at 89-92 C. Student Bs sample melted at 96- 98 C. Because Student As and Student Bs samples were within 4 C of each other, they prepared a mixed melting point sample. Each student recorded the following results: each sample began to melt at 89 C and melting seemed to stop around 92 C. The temperature increased with continued heating. The solid began to melt again at a temperature of 96 C. By 98 C, all solid in the melting point capillary was gone. Explain what happened.
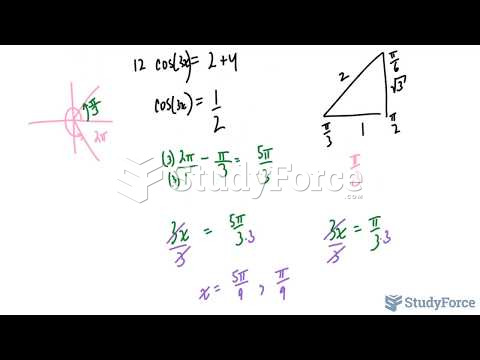
Question 2The melting point/composition diagram for compounds A and B is shown below. If a mixture of A and B had a final melting range temperature of C, what are the approximate mole fractions of A and B in the mixture?
Question 3/pSefPLJIBTJ02Xw67MSAtnTzQrGeZmAXy96LzOFbd4g8O2332phsPjv7Nmz6dJLL3XdsNWrV2t+0K2trdpwOGLUuo48YwaxWIzOP/984l7XqVOn0l//+ldXQ/5lNMSFH7hMHJaOI3Lsueee1NLS4kIuSFIl4NdnJQSyWov4DAJ5EPDrRZ9HEXFoBRHghRS4Z42jFfBqeiyOeeNhaV52uhQb+7f++Mc/1rL6/PPPaYMNNihFtshDIXDFFVfQNddco+1h9wN+URk2bJhyhD8/8kjIAw88QDzhkN2GePvjH/9I55xzjj8L5COr/fqshED2USODqd4i4NeL3lsUYY0XCLA4Tl0UhNs3h13jWMWl3GbNmkXsG3rxxRdTXV1dKbOu6Lx4+WUWi3/+8581DtyDzH7o+n3Oz3DYv5393NXtiCOO0NxGeMVIbO4S0NtQKSb8OlkSCGQnaSKtiiLg14u+oioJhc2JwPXXX081NTXasby0NH9mf9Pvf//7OZ3v5EEclmvMmDFaktyTvdtuuzmZPNKyIfDdd99Zeom5B5kX2AjC1t7ebkTd2GabbTRRvP7662MiaAkr16/PSgjkEjYSZBUsAn696INVCyiNEwR22GEHbclgXmKaw3qVezvyyCPpb3/7G02aNElz99CvtXLbFcT8WRyffPLJRog/jg/8f//3f4EpKi+dzj3hLIqxkl55qlW/ftGDXB7+yBUESk7Arxd9yUEhQ88T2H777emf//ynZueqVavKvlgHD/ezWH/55ZfhJ+pi61HF8Zprrqn5G7OLS5C2Sy65hG644QatSH6M4RyEuvDrsxI9yEFofShDWQj49aIvCyxk6mkCTz/9NHHIK97YvaGqqorY1UKfMFcO41mwc6g59hFta2ujrbbaqhxmBDZPnoTJky//85//EIvju+66i2bOnBm48n766ae0ySabGOXiiYe8MA2HE8RWGgJ+fVZCIJemfSCXABLw60UfwKpAkRwgUF1dTRzeS91YQHEUi3JtPDTOQ+Qch3fx4sWBmDBWLpZqvl9//bW2+AsvDMNbIpEIpDjWy8wxnO2WTeeRCv0+rh+Lv84T0BnDxcJ5tkgRBDxJwK8XvSdhwihPEODetldeeUWLIvH//t//02zi73vssUdZ7FNdLc466ywjwkJZjAlIpsuXLyf28X7ttde0EvFoAS8KEvSNe8ybmpq0lfRuueUWrbgXXXSR4X4R9PKXs3x+fVaiB7mcrQZ5+5qAXy96X0OH8SUj8MMf/pA++ugj4ri4HB+5XBu7WrCPNG/cE/jzn/+8XKb4Pt+Ojg46/PDD6f3339cmrTU0NGjffV+wPAughxLkSaC8MA02dwn49VkJgexuu0DqASbg14s+wFWCojlIYNy4ccS9jV4I+XXUUUdRY2MjjR07lpYsWUIbb7yxgyWtjKQee+wx4+WCfXIff/xxLUpIZZTeWkp+yWIee++9N7300kvWH/HNcQJ+fVZCIDveFJBgpRDw60VfKfWDcuZP4OGHH6YXX3yRnnzySXr77be1BHiC3MSJE/NPzMEzODwX9yJ//PHHWqrwHc0P7lNPPWWZlLZ06VLixTMqaWOXEl4ym8vO7Zw3jvd93XXXVRKGspTVr89KCOSyNBdkGgQCfr3og8AeZXCeAEeJYPGgbnvttZcWak3dV67P7BN99NFHa9mzywe7fmAbmsCDDz5IM2bM0JYO33DDDenvf/97xYnjyy67jGbPnm2BxYvgfPDBBzRy5EjLfnxxnoBfn5UQyM63BaRYIQT8etFXSPWgmHkQeOihh2jatGnaGfvuuy8dd9xxWo+tHvotj6RcPfS3v/0tXXvttVpYMl5I5LDDDnM1P78nrrumcDk4rBn3nK633np+L1Ze9nMYu0033dQ45+677yYegTj11FMRwcKg4u4Hvz4rIZDdbRdIPcAE/HrRB7hKULQCCeyzzz5aTzH7HXMkCy9vxx57LPHkMo7XzBOsOBQdNisBXgDkggsuoDlz5mg/8MtPfX09rbXWWtYDK+AbR6xgFrx98cUX2hLqFVBsTxXRr89KCGRPNSMY4ycCfr3o/cQYtpaGgB6xotxxj3Mp7Zdffkm77767tjT2T37yE3rhhRfKvvJfLnaX6hgWgccffzwtWrRIy3LdddfVlljmxUAqcePFT+655x4aNmwYffXVVxX5klDuevfrsxICudwtB/n7loBfL3rfAofhrhG4+eab6cILL9TSP+KII7ThZ54Ut9NOO7mWZzEJt7e3a7GZWSxvt912mlguJr2gnPvcc8/RQQcdpBVn+PDhdNttt2krIgalfIWUg9vKjjvuqJ3K92yesLh69Wq45xQCs8Bz/PqshEAusMJxGgj49aJHzYGAHQEWVCwc1I19WPUFQ9T9XvjMk8/YV5q3yy+/XAtH5wW7ymXDggULaPr06Ub2zz77rLYCobGjgj/ovcgqAp6UyhFaKs0nW2VQqs9+fVZCIJeqhSCfwBHw60UfuIpAgRwjwD2OLKxef/11I6LFG2+8QbvuuqtjeTiZ0GabbUZdXV3aZCuegMaCvtK2b775Ruv9/9Of/mQUnSNV7LLLLsZ3fCB65plntJUYP/vsM23ZcmaCMG+laRl+fVZCIJemfSCXABLw60UfwKpAkVwgMHr0aPr888/pyiuvpN///vcu5FB8kkIIOuGEE7T4tiNGjNBEEIemq5SNV8TjSYv8EsNbNBqlWCxG66yzTqUgKKickydP1kQyVtIrCF/eJ/n1WQmBnHdV4wQQGCDg14se9QcCuRDQe2fLvdT0ULZyDyqHo3v++eeJY9u+/PLLtM022wx1mu9/Z5eK0047jXp7e7VYvnPnztVeFnxfsBIU4MQTT6T777+feJInLyCCzV0Cfn1WQiC72y6QeoAJ+PWiD3CVoGhFEnjzzTe1njUWD7pwYMHp9V7ZFStWEIeqe/fddzUCHR0dtPXWWxdJw5unp7pU7LzzzsT+2Ntuu603DfaIVR999BElk0nt38KFCzWrzjrrLM3twiMmBtYMvz4rIZAD2yRRMLcJ+PWid5sL0vcngcMPP5yeeOIJi/E8+/8f//iHZZ9Xv/AqgDzxSt++/vprYreLIG38IsBuAZ2dnVqx4FKRW+2yb/3ZZ59tOZhX0GOOG220kWU/vjhPwK/PSghk59sCUqwQAn696CukelDMPAg8+uijNHXqVO0M7nn9zW9+Q1VVVbT++uvnkUr5D/3rX/+qxQBmS7g8PHHve9/7XvkNc8ACriMWxLwyHJfp3nvvJXYVwJadQE9Pj7aojH7UNddcQxzVYsKECfou/HWZgF+flRDILjcMJJ9CYNUKWvZpb8rODF9l2Kl1h4+gdeSb/sh1hmU4qHy7/XrRl48YcvYqAY55/M9//lNbwplDvelt26v2ZrOLh9E5lrO+8bLCfi4P9xqfe+65NH/+fK0c7BbAYe0g8PQazv734osvphtvvFE7iCOejB8/PvsJ+NVxAvr1x5Nq/bRBIPuptgJg6xtzJtNu5y3OvyShMEWnHUVV00+g/bcfm//5Lpzh14veBRRI0ucEJk6cSG+//bbmx/viiy/6vDRE119/vRbCiwvyy1/+kjgEmn69+qlw3Gt85pln0ieffKL5VN999910wAEH+KkIZbf1sssuo9mzZ2ujITyh0Y/toOwQizRAZw6BXCRInB5sAkvmzqDQWfOLKmS4up7m33gijS9zp7JfL/qi4OPkQBK49dZb6fzzz9fKxiuxcWg37lXedNNNfVveM844g+68807Nfvbb5UmHflluObXX+JxzztFEPy8bjS0/Ajwywm2ZN3YZeuihh7Ted6+uEplf6fxxtF+flehB9kf7CoyVTghkDUaohtpfuI62H1k+NH696MtHDDl7lcB3331Hw4alv3GyMPvjH//oVbOHtEsV/nwwT8rafPPNhzyvXAdwPcyZM4cuuOACzQT2B0evcfG1wb3uHAZQ3fbcc09qbm6mtdZaS92Nzy4Q8OuzEgLZhcaAJDMTcEwgcxahOup+62Iql8OFXy/6zLWDXyqZAIszFmNPPvkkLVq0iL788ksNxzvvvEM77LCDb9Eceuih9NRTTxn2L1++XIuXbOzwyIfHHnuMLr30UiNqCEfkWLJkCaHX2JkK4jZQX19PTU1N9O9//1tLlCfssT83NncJ+PVZCYHsbrtA6ikEMgnkULSWTtt6bVqlHf8Nff5JD30kwza1NTZSW0oa6tdofTvNPXFg+EzdX4rPfr3oS8EGefifwHrrrUccKu2qq66i3/3ud74u0B133KFFgOBCsL81LzvMi4p4YXv66ae1hU50W4488kiqq6sjuADoRJz/u/vuu2vLqWMlPefZ2qXo12clBLJdbWKfawTsBXIVtfXPo4npI7zSjlX0/vMP0BkHzCL7qX1Rau+fS9vbnutaMbSE/XrRu0sFqQeFQCgU0now4/G4NlHM7+Xi5ZgPOeQQYv/esWPHaj21/LdcGy/uwe4U6qRIjkPNPd7Y3CVQU1Oj+XQffPDBxC8o2Nwl4NdnJQSyu+0CqacQsBfIEWrpXUh7ZvMnXv48HTXuAGpMSY+/1iS76LrDSx+6x68XvQ1C7AIBjcB///tf4tX0uMeVBRxv7GrBvclB2Fgk84p7vBodi2OObjF9+vSSFY1D6DU0NGgvHCtXrtTyZV9Y7qGfMmVKyeyoxIx4NOStt97SJunddNNNGgJ2uUAsafdbg1+flRDI7rcN5KAQyCSQW6VAnpRNIMs03l9wPm0z/VYltcGPVfXUN+9EWif9F1f3+PWidxUKEvctgcMOO0zzP1YLwLF2dX9Ndb+fP7Pg5ygdt9xyi1GM9vZ2I9KBsdPBDx9++CHxhEcO26Zu/CJy+umnq7vw2QUCLIh58ZvUze8xslPL49Xvfn1WQiB7tUUF1K5iBDKtWkIzRoRofhqb8rhZ+PWiT8OHHRVPgGf46/F1t9tuO/rZz35Gp556KvFS00HdXnrpJdp3332N4vHSwxzVYJdddjH2FfOBV7zjRSrY3/njjz8mPQYsv4jU1tbSHnvsUUzyODdHAhz7eIMNNtCO3nDDDemYY47Reo0nT56cYwo4rFgCfn1WQiAXW/M4Py8CRQlkWkl/OWoUzUrzswhRY2crTd28DI7IeZUeB4OANwn8+Mc/1nxyeeIaR3molI0jd3CsZF6dTt222WYbLeIBT+bSH+7q73afOa1XX31Vmwz4wQcfUF9fnyGKOQ7vjBkz6IQTTqAtt9zS7nTsc4kAu6/wCwnXI9dRrvXpkjlI1kcEIJB9VFlBMLU4gUxkfz5RrLWHzp00OgiIUAYQKDkBfanp/fbbLy1ebMmNKUOG7A/Mrg7c0/vCCy8YFowbN07rUa6qqtIWTeGYuaNHD9xn+EVi1apV2hLd9913H/3rX/+iL774wjiXXzq4B57P/fnPf27sx4fSErjooovoD3/4g7ZIiO73XVoLkJtfCUAg+7XmfGq3vcCNUC4+yFxk+/MhkH3aHGC2RwgsXLiQfvGLX2jWHHjggdrEtVmzZlVkDF7u/b399tu1pbc5JnR/f39OtcQuGhwlY9ddd6VIJEIcBQRb+QnwxMjhw4drhvAIydlnn629DG222WblNw4WeJoABLKnqyd4xtkL3GAI5GxDd7r/oVqj+R7P5wbpnCCVxY91o7ZJHnpOXUmP6+faa68lDomlb3qdqeem/qZ/V//aHc+/6+mpx+qfvXxOIpEgXkCFYxbzctxrr702bbHFFrrpaX+9XJZy2laq+md/b15qXN24V59fDDMtP14q20qRTynyYLaF5KPWiec+y4sDGwiUjEBbvErIiyDlX0S09uZmgv35JKSLRW4JuHhUernMctplm+14GY7I7pQUbmb6nJaM75r3ObYnyJ3ZbHPqnGx5LF261DabbOfI0F15n2N7gtyZLR+/nSN7QG3Lk1oOGQZLnHzyyULG4RXyQWec09XVpR0qZ/wb+1LP5e/ZmPG5dlu2c+yO532lOOftt9/OO59S2FWq8ste17zLz+0kXwbZjneyzTC3K664QkybNk3IlxnDzttuu41/st2y2WZ7gtzp1XO8alcmjl7Zjx5k2XKwlY5AkHuQS0cROYGAuwT4Wb/xxhtrE/Yefvhhw/3C3VyROgiUhgC7wvCS0xzRYsGCBaXJFLn4jgAEsu+qzN8GFyuQ35h7FO12VmMahFiLnKS358DkmbQfsQMEQCBvAvpKeojVmzc6nOBxApdeeqm2nPfhhx9OyWTS49bCvHIRgEAuF/kKzbc4gZwpzFuYkl1P0uHjEeatQpsViu0QAY6HzCvMTZ06VYvKwMm+99579KMf/cihHJAMCJSHwD/+8Q/69ttvNWH817/+VTOCF4z5/e9/Xx6DkKvnCUAge76KgmVgUQJ51bt0/ogdKH0tvWrq6L+FtoY+DlZjQWlKSmDMmDHU09NjyTMcDmsLXVh24gsI+IwAR66Q/sYWq3lyJYfmC8oy6pbC4YsjBCCQHcGIRHIlUIxAXiaXmt7CbqnpaCP1z51KpdbH7Lt23nnn0bx58wirMuXaAnCcFwm8/vrrxIti8MZ/R40apYXD0kO/edFm2AQCuRDg5aS/973vaYfyXw5jyD7IanSWXNLBMYUT4BEoXoznwgsvLDyRMpwJgVwG6JWcZSaB3NK7kPYcmYXM8udpxrgDbJaZLl8M5GuuuYbkzGjikE8zZ87MYjx+AgFvE9hrr73olVdeofHjx5OMRuBtY2EdCORBgBdxOemkkzSRzMtOr7vuunmcjUOdIMAvJtOnT6cHHnjAieRKlgYEcslQIyMmkEkgt/YtpEnrpDJaTatWrqC3Ft9P0ch51Jb6M38P1VH3WxfTWLvfXN4HgewyYCRfMgIsGnhp5GOPPZZ0/8ySZY6MQMBFApdddhnNnj1bGxVRVzp0MUsknUIAAjkFCL6CgB0Be4Esda70dRyjnvDZZ7S4zVYSq0dRnYxecXGZoldAIFuqAl98TEDvZeMiXHzxxXTAAQcQz/DXh6Z9XDSYXuEEZHx0Wmedgd6XffbZR2vf+++/P2200UYVTqZ0xYdALh1r5ORjApkEciFFCtUkqfW6w0vue6zbCoGsk8BfvxPg2f28Gpy68UPt7rvvJrl4iLobn0HAdwR4lcNly5ZZ7I5GozR37lzLPnxxhwAEsjtckWrACDglkMM1DdR43TTK5rbsNjoIZLcJI/1SEuju7tZ6jXlZ3jvvvJN4+WneeD+HfsMGAn4lwG356KOP1vyPn3jiCZKrjmpFueeee/ACWIJKhUAuAWRk4X8CxQvkCCWabqKZk7cuOwwI5LJXAQxwicDKlStpwoQJxH8bGxu1uMguZYVkQaCkBDiqxS677EJLliyBz32JyEMglwg0svE3gSV/mUGhWfNzL0QoRJHQXrTb7nvTvvvtT/tM2prS5vLlnpqjR0IgO4oTiXmMwN57700tLS3aMDQPR2MDgaAQuP7667Uwb4ceeihxjzI2dwlAILvLF6mDgOcIQCB7rkpgUJEE3n//fVq6dCmxIOa/vL399tu00047FZkyTgeB8hL4+OOPNXehc889l3jFSN4uuugiuuGGG8prWAXkDoFcAZWMIoKASgACWaWBz34noMdCVsuxww470DvvvKPuwmcQ8B0BFsGXXHKJxe6RI0fShx9+SBtuuKFlP744TwAC2XmmSBEEPE0AAtnT1QPj8iDAvcQTJ07UzuAlpzfYYAO6+uqr6cQTT8wjFRwKAt4jIISgNddc0zCMfetPOeUUrX2r+40D8MFxAhDIjiNFgiDgbQIQyN6uH1iXO4GDDz6YnnnmGW2W/1dffZX7iTgSBDxO4N5779UEMZuJiCzlqSwI5PJwR64gUDYCEMhlQ4+MHSaw2WabaUtMs68x9yZjA4GgEJgxYwbNnz9fi/O9atWqoBTLV+WAQPZVdcFYECieAARy8QyRgjcIXHfddXT55ZdrxrC/5jHHHENbbbWVN4yDFSBQBIE2uSLrzjvvrKXAsZCvvfZa2nbbbS1uF0Ukj1NzIACBnAMkHAICQSIAgRyk2qzssnBsWPY9/vzzzy0g/vCHP9CFF15o2YcvIOA3AgceeCA1NzdbzD7ooINo8eLFln344g4BCGR3uCJVEPAsAQhkz1YNDCuAAIvj3//+9/TWW29Ra2sr9fb2aqnwJCdsIOBnAv39/RSLxaipqYm4R5lDvvH25ptvGr3Lfi6f122HQPZ6DcE+EHCYAASyw0CRnKcIjBs3jpYvX05PP/008SQ+bCAQFAKRSIQeeeQRmjlzJiUSiaAUy7PlgED2bNXAMBBwhwAEsjtckao3CGyxxRa0bNkyuuyyyzS/TW9YBStAoHgCp556qiaMd911V3rjjTeKTxApZCUAgZwVD34EgeARgEAOXp1Weom++OILbQW9K6+8kh599FENx3PPPUcHHHBApaNB+X1OgMMXfvrppxSPx+nGG2/USsNC+a677vJ5ybxvPgSy9+sIFoKAowQgkB3FicTKTGDWrFn0l7/8xWLF+PHjtfBvlp34AgI+I3DffffRSSedZLF6+PDh9O9//5vYlQibuwQgkN3li9RBwHMEIJA9VyUwqEACPMOfZ/rztv7669O+++5L4XA4bXneApPHaSBQNgI8+XT06NFG/tzOeQl1nrS31lprGfvxwT0CEMjusUXKIOBJAhDInqwWGFUAgUMOOUSb4c+nrl69mviBhg0EgkCAJ+GxKwVv77//PuJ7l6FSIZDLAB1ZgkA5CUAgl5M+8naSALtSfPLJJzRp0iQtxJuTaSMtECgngeOOO44efPBBGjFiBH399dflNKVi84ZArtiqR8ErlQAEcqXWfPDKffHFFxsTl3hFPZ6kh+Hn4NVzJZbo5Zdfpn322UcrOq8O2d7ejrZd4oYAgVxi4MgOBMpNAAK53DWA/J0iwAsppAri9dZbj6666ir6zW9+41Q2SAcEykKAfY7fffddI+9hw4YR9yzzpFT+jM1dAhDI7vJF6iDgOQIQyJ6rEhhUBAEWyb/85S+1JXk7OzuJv/PGq45tuummRaSMU0Gg/ARuvfVWmjt3rtae9VUi+Xs0Gi2/cQG3AAI54BWM4oFAKgEI5FQi+B4kAuussw598803dPPNN9P5558fpKKhLBVOYMcdd9RcLTiixbPPPlvhNNwvPgSy+4yRAwh4igAEsqeqA8Y4TIBXGXvzzTfpiiuuoNraWodTR3IgUD4C7GN/9dVX0+67706vvvpq+QypkJwhkCukolFMENAJQCDrJPA3aAQWLFhA06dP14r1wAMPaP6aQSsjylOZBNgXeeedd6Zvv/2WjjzySHrssccqE0QJSw2BXELYyAoEvEAAAtkLtQAbnCLAQiESidD//vc/I0mewMShsXjVMWwg4FcC7FO//fbbay5Da6yxBgkhtKK0tbXRxIkT/Vos39gNgeybqoKhIOAMAQhkZzgilfIT+OCDD2jrrbfWDOFoFptssgltsMEGtGjRIuIYydhAwK8EUiO0sP8xT9KbN28eHXTQQX4tlq/shkD2VXXBWBAongAEcvEMkYI3COy333704osvasYgaoU36gRWOEMgHo9r0Vk4tYaGBpo2bZozCSOVnAlAIOeMCgeCQDAIQCAHox5RCqItt9ySeBj6iCOOoMcffxxIQCAwBGbNmqXFOx49ejT19PQEplx+KggEsp9qC7aCgAMEIJAdgIgkPEGA4x9zTxtvHPaKw19hA4EgEHjhhRdo//3314pywQUX0E033RSEYvmqDBDIvqouGAsCxROAQC6eIVLwBoH//Oc/lsVAOAbyiBEjaOHChXTAAQd4w0hYAQIFEFi9erVlkin3JPPEU75/Y5XIAoAWcAoEcgHQcAoI+JkABLKfaw+2pxL497//rfW0ffLJJ9psf/13HpZmUYENBPxKgEO6HXbYYfTSSy8RR7HgBXB448gtHOoNm7sEIJDd5YvUQcBzBCCQPVclMMghAhwrlmf7czisOXPm0K9//WuHUkYyIFBeAl999ZUWmYUjWfDoyHPPPVdegyogdwjkCqhkFBEEVAIQyCoNfA4agUmTJtHf//53rKQXtIpFeeh3v/udtjrkHnvsQa+88gqIuEwAAtllwEgeBLxGAALZazUCe5wi0NLSQnvvvbeW3P3330/HH3+8U0kjHRAoKwF2Jdp88821BXF+9rOf0aOPPlpWeyohcwjkSqhllBEEFAIQyAoMfPQ9Ae4tPvjgg+mLL76wrKanrzrm+wKiABVLYMWKFfSTn/yEli1bRt99953Bobu7m8aOHWt8xwd3CEAgu8MVqYKAZwlAIHu2amBYngR4cZAJEyZoZ6255pq08cYbaxP27rjjDho1alSeqeFwEPAOARbEvGS6vo0ZM4Z22mknmjt3rrb8tL4ff90jAIHsHlukDAKeJACB7MlqgVEFEDj00EPpqaee0s7kCXrbbbddAangFBDwHoF77rmHZs6cqRmGCaflqR8I5PJwR64gUDYCEMhlQ4+MHSbAPpkffvihFgpr0aJFDqeO5ECgfAROOeUUuvfee2nDDTckdrXAVnoCEMilZ44cQaCsBCCQy4ofmTtI4OSTT6Z58+ZpKb799tvaELSDySMpECgbgaamJjrkkEO0/P/4xz/SOeecUzZbKjVjCORKrXmUu2IJQCBXbNUHruBLly6lrbbayigXr6LHfshPPvkk/ehHPzL24wMI+I3AqlWrtFUhdbu5bfNKkeyDPH36dH03/rpIAALZRbhIGgS8SAAC2Yu1ApsKJdDW1kY//elPtWHo/v5+LRmesMfD0pioVyhVnOcFAhyZZZ999qEPPviAWDDrGy8SgqXUdRru/YVAdo8tUgYBTxKAQPZktcAoBwg8++yzFA6HtZQ4ksXpp5/uQKpIAgTKT+A///kPbbnllppQ5rCGTz/9dPmNCrgFEMgBr2AUDwRSCUAgpxLB9yAR4FXGXnvtNW3FsSuuuCJIRUNZKpyAfu/ec889iRfFweYuAQhkd/kidRDwHAH9JptIJIwwQp4zEgaBQAEEurq6aLPNNtPObG9vR7zYAhjiFG8S+Oqrr7SV9D777DO69NJLafbs2d40NEBWQSAHqDJRFBDIhQAEci6UcIxfCDz++OPai96XX35p8dPESnp+qUHYmYkAr6A3efJk+uSTT6ivr884rKenh0aPHm18xwd3CEAgu8MVqYKAZwlAIHu2amBYngS4N42X3GUxvMYaa9C6665LO+64Iz388MNGT3KeSeJwEPAEAW7TvHqeHgOZo1iMHz9ei2LBPsjY3CcAgew+Y+QAAp4iAIHsqeqAMUUQmDZtGj300EPakrzcy/b973+/iNRwKgh4h8AjjzxCkUhEM2jx4sV00EEHece4CrEEArlCKhrFBAGdAASyTgJ//U6Ae415O+mkk2j+/Pl+Lw7sBwGDwIwZM7Q2PXz4cPr222+N/fhQOgIQyKVjjZxAwBMEIJA9UQ0wwgECv/3tb+naa6/VUuKV9LbddltiQYENBPxOgEdE2KWCN3YZ4lX1Ro4c6fdi+cp+CGRfVReMBYHiCUAgF88QKXiDwH//+1/NB1m1ZueddyZeSGGDDTZQd+MzCPiOgD5Cohu+ySabELte7L777vou/HWRAASyi3CRNAh4kQAEshdrBTYVSqC+vp6qqqqIH2bfffedlsywYcPo888/p/XWW6/QZHEeCJSdwHvvvUfbbbcd8cqQ//vf/wx7WltbadKkScZ3fHCHAASyO1yRKgh4lgAEsmerBoYVQWD16tV022230Xnnnael8vzzz9N+++1XRIo4FQS8Q+CJJ56gqVOnav7IM2fOJI5jj81dAhDI7vJF6iDgOQIQyJ6rEhjkIAE9skU8HqczzzzTwZSRFAiUl8CCBQto+vTpdPjhh1MymSyvMRWQOwRyBVQyiggCKgEIZJUGPgeJwL333kunnHKKVqRnn32WDjzwwCAVD2WpYAJvvfUW8RLT33zzDZ188sl0zz33VDCN0hQdArk0nJELCHiGAASyZ6oChjhAoKGhgY499lj6wQ9+QB999JGWIvsg88pj/BcbCPiVwD//+U9tufRx48ZRd3e3UYx3331X8002duCDKwQgkF3BikRBwLsEIJC9WzewLD8Cvb29RrQKDu/GE5l22GEHLYrFRhttlF9iOBoEPEZAjWLBYo3b9N/+9jf6yU9+4jFLg2kOBHIw6xWlAoGMBCCQM6LBDz4jcOGFF9LNN9+sWb18+XKspOez+oO5mQksXbqUttpqK+2Axx9/nI444ojMB+MXVwhAILuCFYmCgHcJQCB7t25gWX4E9B62X/3qV/SnP/0pv5NxNAh4mAD7Gc+bN49GjBhBX3/9tYctDa5pEMjBrVuUDARsCUAg22LBTh8SOPvss7XQbvwg+/TTT2nMmDE+LAVMBoF0AnoMZP7l1VdfxeIg6Yhc3wOB7DpiZAAC3iIAgeyt+oA1hRPo6uqizTbbzEhgrbXWonA4rPlp8uIK2EDAzwT0ERIuA7ftLbbYghYvXmwsQe3nsvnBdghkP9QSbAQBBwlAIDsIE0mVnUBdXR1deumlNHLkSFq5cqVmz7rrrku8DDUPT2MDAb8SeOWVV2ivvfZKM7+9vV2LbpH2A3Y4SgAC2VGcSAwEvE8AAtn7dQQL8yMghCDubZs9ezZddtll2sktLS1a3Nj8UsLRIOA9Aty+n3vuOTrkkEO05dTPOOMMuv32271naMAsgkAOWIWiOCAwFAEI5KEI4Xc/E9BX0mMBwUICGwgEhcBDDz1E3L6xkl5pahQCuTSckQsIeIYABLJnqgKGOEigv7+fHn30UW0pXo6H/OSTT9JPf/pTB3NAUiBQPgJvvvkmHXDAAZob0UknnUTz588vnzEVkjMEcoVUNIoJAjoBCGSdBP4GgcBLL71EkUiEVq1aRV9++aVWJHa34JX01l577SAUEWWoUAIcmYWXl+Z2/dlnnxkUXnvtNSwWYtBw7wMEsntskTIIeJIABLInqwVGFUCARXHqRDyOavH0009jKd4CeOIUbxFQo1iwZeuvvz7dc889dPTRR3vL0IBaA4Ec0IpFsUAgEwEI5ExksN9vBNRJeX//+99pwoQJNHbsWL8VA/aCQBoBXhly3Lhx2v4///nP2kp6P/zhD9OOww73CEAgu8cWKYOAJwlAIHuyWmBUAQSi0SjdcccdNGfOHPr1r39dQAo4BQS8SeDBBx+k4447jqZMmaLF9famlcG2CgI52PWL0oFAGgEI5DQk2OFTAh0dHfT6669rQiJ1ONqnRYLZIKAR+OKLL6ihoYF4Ql6qGxEQlYYABHJpOCMXEPAMAQhkz1QFDAEBEAABEPAoAQhkj1YMzAIBtwhAILtFFumCAAiAAAgEhQAEclBqEuUAgRwJ6AJ5+vTptMkmm+R4Fg4DgfITCIVCdPrpp+dlCFwv8sKFg8tIgFfMy3e79tpricPBYXOeAE+OPOaYY+iBBx5wPnEXU1xDNqT8W5KLBiFpEPALgZtuuoluu+02+uCDD/xiMuwEAY3AxIkTqa2tLS8aEMh54cLBZSTAC9zk216HDRumLT9dRrMDm/V6661HZ555JvEz008bBLKfagu2eorAihUriP9hAwG/EeAH1sYbb+w3s2EvCLhGYOnSpYT+Qtfw0siRI30XOhIC2b32gJRBAARAAARAAARAAAR8SAAC2YeVBpNBAARAAARAAARAAATcIwCB7B5bpAwCIAACIAACIAACIOBDAhDIPqw0mAwCIAACIAACIAACIOAeAQhk99giZRAAARAAARAAARAAAR8SgED2YaXBZBAAARAAARAAARAAAfcIQCC7xxYpgwAIgAAIgAAIgAAI+JAABLIPKw0mgwAIgAAIgAAIgAAIuEcAAtk9tkgZBEAABEAABEAABEDAhwQgkH1YaTAZBEAABEAABEAABEDAPQIQyO6xRcogAAIgAAIgAAIgAAI+JACB7MNKg8kgAAIgAAIgAAIgAALuEYBAdo8tUgYBEAABEAABEAABEPAhAQhkH1YaTAYBEAABEAABEAABEHCPAASye2yRMgiAAAiAAAiAAAiAgA8JQCD7sNJgMgiAAAiAAAiAAAiAgHsEIJDdY4uUQQAEQAAEQAAEQAAEfEgAAtmHlQaTQQAEQAAEQAAEQAAE3CMAgeweW6QMAiAAAiAAAiAAAiDgQwIQyD6sNJgMAiAAAiAAAiAAAiDgHgEIZPfYImUQAAEQAAEQAAEQAAEfEoBA9mGlwWQQAAEQAAEQAAEQAAH3CEAgu8cWKYMACIAACIAACIAACPiQQDAE8qoVtKyrh2jERrT5+NGuVsOKZW/Q86+9S19+S7TW+hvRVjvtSZO2djfPQgq0asXH9GlvP9HwUa4zKcQ+4xyuu097ta/DR21M40evY/yEDyAAAiAAAiAAAiBQDgKBEMgr35hDo3Y7T+OXaO+lmduPdIXlkvvOpNBJt1vSrkq007yZ21v2lfrL6hVL6OZL76dD/nAdTRos+htzJtNu5y0mCsWo561zyXsSfoDS81fvTAdc2TbwJZyg3mdmkju1V+paQX4gAAIgAAIgAAJ+JRAMgbxkLo0KnaXVQay1h86d5IIcXLWEZowI0XyjpkPyUxvF23rpzInlk3Sr3l9AI7aZLm2JUGvvQkUgHyUFcqO3BbJkeqZkar5yhKihs5WmbT7MoFzuDx8/cwNNOb+exux1CTXOPbFA8b6a3n1+Id07v5Fa/tUlizSKJvxoN5py3FF09OSJhD5zrmU3GK2kNxY9RPPqF9JbXQOjFKMm7ExTps+gE6dOKrAuy90ikT8IgAAIgEBJCIgAbL1tcSFhaf+kQHanRL0tIjKYR1WsRfRruQz8706GuaVqlj0iWnvNc7qaE6KmpkbEGloHbTV/88qn7qZao970+gvXNXvFPCG6m0R4sM4pHBcFtaz+ThGLDLRNvYyWv5GY6PJOictjiRuMelpFdSgL91C1aCmoQsuDCLmCAAiAAAiUlgCVNjt3cjNFIgm3BHJ/e8IQc4n28gtjnaRpV5Vo845ZunlZ/vaKhC4cw9Wipio0yFeWoy/LaSX6qb+rWVTp4pj/SoGsvH/kaEW/SNbo5WKxFhI18XqRiFUbbUkTy9WNnn2JybGgRRzmBqNuEQur4lhyjyVEIl4j5LiPyT5Uh5eTImoOp4IACIBAkAk442Kx6n2ae+NdtIx+TGdWT6EPH7qDbrq3npZ+Jh//NIYmn1ZNF0Wn0ng5lrzkkTl0xa13Df4mJcOR59NVNTNp61QvhdXL6ZkHE5R4cBG1DSREY7bci4469VSaNXVPy/DoyqwuFivplQUJ+r/b7qI2zR5pkZbOmRSVw6xDDm/Lsv3lxvvovZ5Wmn2rdFmQWyRaS/ts1kcb7H4aHT3hHxS/v4V+MOVkCn3aQL+5egF9JsscOvI4uvyi02j70cNo1cdL6OEFCyn5zGKzLGO2pB/tNZmOO/kEmrz9WC1dy3+y/M8vvJ/mz19ILUr5Tz7rHDr+cB6WX0XPzJ1DT7/xEs2+ne0KUbT2JNqs7xva/bSLaIdlD9DcF9+jEeMOoYvOnGwtZx5syajbbemcmuPpowdvpJq6BbRYy1GWc/JRFD1nBu2f70TFjxfRzhOmSCcVyTPWSnfs+TSNk24MvNUkO+m6wzfXPpfjv/efmUPbHDzg0z7gSCOtCMelf/SZlnY3lG2rlz1Cw7eQ4w7aVkVNXQmaPH7AfWTVskV0/BZTaKBFETV09NG0rYdsjUNl6bvf3WC06t25NGKHswZZRKmlZy7tOXrw64o36PyNdqNbB7/GWnulS1bqzcd3GHM2ePWKd2nhvHup8Zl3qKu3l0aNmkA7Tp5CJ5xwNE0cW2j743vsfXT3/CT9S6bJ26gJe9Gxs06AC5FGww33IS1hy38rl9xHv7oiqe2LXH8bTXNpLo4lUw99caNtL3/3eXq44WFKLn6LBls2Tdh5N5p+/Mk0dc/yPaM8hJ3c4O6Oy10B1BxR/72thvuBNMHsoVE/R2pFvDZi/xtFRbvSa9jXmcyeXqhGqJ4UGXuQe9pETbZh1nCtJV9bFn2t5jC7Wh75OVT3jIhbeqqsZU/IQnUm6zKU2Ty2NtlpybpfDu3r7hy2PMN1orO/V8QylK1Ojh23xgZZh2MW14B82Ypc6layiOc5Xt0WrzK41HfIru/+NrPHNsVmCxwXv/R1tohaoyfb7PnVeh0L6EFu0etA8qlt6k6zvLvZbBvyJSHt90rY4Qajjgazh746me7A0qNyj1cO984ms73Z3VdizemshmyD3S3ZXVnkvapDubcPmV7QDnDDfciOUV+biCrPJ7dGUu2y9sI+59t2j2ioCRvPKLvrhapiorOS27aseOe5y0RLdc3k0HCdcbGQItIyHE0R6fuaFM3JuI3QC4vaWFzEE3FRrYjLqvr2AXP72y0XeqiqVjS1tou2lkbL8SSHR3XJYS+Qu0WdKiClQE+2ton21iYpgkxxSpHEkEPnnfIc1Y80WlcvGhsbZHrvmW4C+s0pXCUiWr7Svp5mi7iuiTeI1nZZFpleXVS5+CxDvSl26+VvbhBRpTzRhg7R09kqYkZZQqKuvlE0Nsg8uvqEIUBVYVcAW5FWt2FRl6gXDQ31ipiUPPPy0e0UNTovpR6bak0m9WV4qrbGzPz5hlhdW2PeIFWOOVxYQr6WmC9PEdFi558hH2rGdROqFdbXpJwy8flB7jBSBXJts36XMFH1KXMWKuXFpL8raXEvCVXViPr6hKjW3Zy06zEkGjvz8NOSL89G+9XOj4jaeELE66LmdcP7pQtRZeoIN9yHzHZsfuoTjdXmCz3fuypJILvRtpvrrM+CcLRWJOrrRV11SidfVX2Ftm2pY924p0hnQy+5JbogkKssYqBP8d2V49Qiqd6AFQGpP6g66s2ba7i2KcU3s0fUR80bQW3TQI+HnUDuaTF7S0I1qTfoPpFUxJiMRGHeazJ86u+oN276ccNJVvGjlTclnrw3sPWJnt5+0dFglkW31Uy+X7mpmQKqM2mKsjS7LQK3VntB6O/QfaOtPsh2ArkQtlaBLOvWMrGpRyQMgW6WwSyj/afe1pjBMqq/GMlD1bYSqmmyP9nFvW3xgZtfqKpOtHSxUGg3BUC+All9scj48tAr4oZAyZ2fiwhKm7RLjFQBLP13jBfpgcL1Wu4hPNoS/E0+dBQBFYk1K/fVPtFUpzz0ow3Kb9nJNCv3UKpKWDj3dTQqnQMhkdSup+zpBe3X/s5G4z5HVCWaFAapI3nSxarg4ncl0yc7V45AdqFtyxFcc65CSCRarS/Zve0NStsmwSPFlbe5wF1CLNU1k2t9OS6QI6lDlkovWbg2NUKBKTAHBLL8bgiuqP2kM0VUh6SA5i1dIKvis0q02nWK9LUYjTycw/B2eh5azkoPsjWKBP/a09Eqe3TrRSxWbzMZqF+Yw8vmubpIk565otnm2d3eUCui1dJdpT4p+H5r2mWmwXmnC+TC2KoCWcZ85qQtm5GPtFeNomE5yPJFrZtUUdijTK7KNT1L4sV96e8W7R3KzVDtIStGIFdlGqXoEw1RfTSjDOUtjlbxZ6sC2UlG/R3mCAX3YMpJoI0t1tGjgQdgNMc2W3xRy5qCvGcaLltypCLdkUKOWhmjeanXZAbLVZcoKf6MPgPlcHVEpk71iVOOCfJH8/7uoouVHmnHGF0c6ECqGIHsQttWXd+qUvXMYIPtbDQ7stROniC3Z0vZXODO6ZfkmrEUJPsXxwWynPRizVF5CKaJZ+nckBjsQdMFstGjJnsy7N/LzHNo0FfVFIn60JLaM0ciEq0W0WhU+Se/Gz138ncnBHIkW5QD6Yvc1iKS0i0jEasTNdEq5Q2VBZIujmTvlv6CkDU9E7FZdj2Ngd8M4WoIO4VJHmxVgWzX097TovcGW/M3LUz5pITLI+l73tjcIpqbm7V/La3NopYFzeA/diMp66a03byjWCi+25F4W8ZitCV0X+wc+WVMyYc/uMqoU1QrbUlvU+bfyuGtjthkuteZ7ZCEnCQ7ZGPqUkI02r04awn0dMjrukW0tUt3MPub+ZD5+PcAd9yHrDxkHsZzLCyqIqZbQKUIZDfaduvgSOKAq0qKnhmsAHW0M2yMHFtrJ8jf3ODuRbdEFwRySrenIjLSb86m2B34zQzPFKrV3RVSm5l5Dg2KSFMkmgJZF97mA9EUXmn7QtaJbKk58vf0PLS9hsDPJKDaZI9vWn5pD279Ya2IWEPY2llj7jPt0tMY+C1dIBfGVhXIdjfdTPmbFlo/qf6hQ3JR/JOtqZTom9J2M9VvRkuUSTOhmtSRE/Mso56MlyTzt8B/co2RHJ2JmxP1MrWzaFx1NQgubbON6ffH9LKa1zGJXEbUjEnA8l7WMKine7o6RGtLi2iR/1rbOzN0cKTnHcg9KfeOlKfiYJGV+728/m3nKWSBo77UVDd2iHbFPdHuXp0lKd/+5EbbZhj9fb2ip7s744udyrq63B05Zag9V7iX4JrJF5XHBLL5RpzZB1URyIO+nerNfeDGoBwjb+CJZJNIJpNpjZgK6QAAIoNJREFU/5qamkRTk9zf3D7kzTw9D0at5GMjaNVeFu0hHYpo7hGxRINokb0qjUaMXF3cKjdMx3uQC2PrrEA2RfoAj5AIhdL/qYLGrtc630Ze8PEpF6x9X0KG1JVz018MzXPMG43eBszfAv/JJUbqw4vbUm19s+ju7RN9vd2ipcGcm8C/VSUy9+4Hhb/ZxuS9MMN8i752c45FtvaqMzHTjIrmdhn9xejJVDsiqkRDm+KypJ9cCX+Vts3+2fb3jsJdrPo6GsyOF/ms4A56s04yvwgFDb1aZqfa9pCMLKOg7INsX7tDpuPjA1zh7vI1UwhujwlkRSDa+srJIkr/QmPotGrgxpMuXhXhmikdORWls61VG/7rlhPqhtrS8+AzlHzSBLJSFrlARLwl3fOvPW14XXV8r7GNatDdPODSEArXaH5/pl3S11oZxjQasGGXYk8mJjZsnRTIfcpEx1B1MuNkIMsKe+VcREO9YA2OQ7WUwd+Vc7OtDthsTJCqbIHsGCO1DUsBHLfxfe1VxCC7+Xho3Z8cG1d+hxn3AukrrN4jLKkoc0WGFsiKK5hkrL7Q2n2uG5xMbckv6F9cdh8yogDJnmd9ropZz5UokJ1q20M1zC7FX1+2/RyiYA2Voh9/N9uag9xdvWYKo+wxgdwv1FBfdTYhmtQhej00nCkSzRuDKT5J2DnRdzebrg+huqFjodrlMZRANtw8pLhStOtATckHkiH0leF1NfJFTVoM137RoPsoDz7sTLs4RJPZCIwGbAi7wtg6KZDVWe/xVF9103T5EqSG+gsbDwD1kJJ8VkRu3i4WysWe+VzlpaWAIdaSMHAzEzcYqb07WUIwqfeZso5SuMl3MO32hB5NJySa7Mf6ZQgZM2RbLgLZ9H3VBXJYxJOtMrRlj+hqbxI1xqQ//j3LQ7QE5S9LFq65DwnLM1J9Rhj3fPnSUikuFs637WytpVvEjecvt+uwaOoeunMtW4p+/c0V7i5eM4Vy9phAlsWQsfXUXoi6xrYBcdnfI1rqzZmjPLFNj9BkikTlxqBEu+D0qhPNokdry32iozlhRLDg5X9zif1pm8dQPcjGQ0L2IDd3DPaY9ovujuaUB4jif6Y+4KXddclB94++bpGM6Q86eXHWDPTA9rbGDV6R2nrR2tYuuvv6zeE2QyAXxlZ9cNrddE0uQ/SA9qmi1753XG3ELUocyrINgyuiIbPIVa1WPqsiX/bYK+8uykFdolaffZ7xGOXwoH10gZHZHvkayeL7bYzeKPeMoPEdLI8pnJT7TGpZlbaei0A2Xv61HuSIDGGWmqB0p1LcLsp2DaeaVarvOfJU6yZbn4FutjkpWrbvlNE1M63gt2mdh1lmp9q2nnLK3/5OS3tm3VCfwV0p5cxAfnWFu0vXTDEV4JhA1sMIpYkopZco/cZruiiov7UrK2GpYln9XKes+qQ+FNX8O23iQ6pp8OdsQ7sqWHXWppmHaT8LqNTOGTUUjJYv+9tqDxR++7T+i+lqX2Y6tN1meKr+TsUXbTBNXhzBaMApduXLlgVyxrqVtprsswtk1R9brWuVsfq5X/WxIymoy/GirlyweQtk+TqkBu9vsCtAlxIntSpT1BaVStA+u8BIaa/6JF47aupoRn3A45ga9wJlOD6NSbe5qNHQ16c68mE/QsfpqzP9h04zzSJ/71DuHdmeMXm5WMlnqbkwi+yVT3F9bVVWJzWfUf7GOJT1zrft9Bz7u1osi5dVujhmQq5wd+OaSa/OvPY4JJD1FcHkW1Xqw0a+eenLPWcN85YSb7C7rdGycpwuKEORGpFst0pRU6Sl+xz2yuE+dcU+PR2SE+bisnc2Z92lx5uUItT0azQFcsh2tSjZkysnBdmJ4midjGOsXHipD5Cedll+owfaFNPh6rhInRPQkhiYsR+ODAT851noxgxnm5Bu+bAVhm+iTd3KptbXZi5UknrDVluiOaSdW4+9FvLF6IEKiWIC6at25PVZuWCzCeS+3l7Rq/3rs7Qn1Y2HovUpE3XkBB1l8Yb0hWTystS3BxfDyJa72istr1U7N60+GejfuA9kiOHrW6A2hpux1blnMUVVDR6v3kPzjWJRY+MKpyVr3Dvk/SvlRd3GzGDtUjqGMt871BeNLD2geh0pCyxx+w3po0+DHSNmmzafF+nP3GBhdqNtq4R6WutTnt8RudhZmsOkekpFfHaFuwvXTLGV4YxALtYKnA8CXiSQk0CWDznjRSZsDdUkJ4xFlYdXKJoQHT1STMv4sAlFHBP3kHux/KWwqWBGmbmrfvwsGmoSTaKzu3cgikWj9YU1UgExTNUVNDPFOFZXY1P9WjM1ATVWrN1y3tp5ikAODbqEZUovcPvVF7WM7lP5uVipo5h2YthuXy4vO35m70bb1nl0t5juixrbcK2oYK8KHYv21xXuLlwzFqML+AKBXAA0nFIhBFLeaK3jFjqD7L1APUYPu9mrk/ogM0ck9DQr629hjLJx77X0zqfyNr7L8FiVEITMsnxrit+q3tLUpajrc1j2WBXU+oqmelr6X8v8iBwWY9LPC8Zf592H+jqbRV1tnVyZNWb7rzoysIoet+9ItTyurk4kmoL96u1G2+b215t635adG5Vwr8j12nOHu/PXTK7lyXQcBHImMtgPAtI9yJhEJ10k7AfWpJuNMbNZLo9uc1BfZwY3H7kEcqq7UKVCz5/RUNyle1MypkzGVV9QwqK2oSVDfQaxBmRoKmM4nl2lrG4WHAPZcANLDQHZ3zfoPiRHPuTkX2NTe3ukIEtNU862VpaNt3d1MdIK6Idi3IfkShX23LOwUiM3xe1uRFnO9e9PLrRtJZqC9rJRmzkkqX+5FWt5Edxl1rbucXJ/UddMsUWyOR8C2QYKdoGA8wRk9JJOudpVe7v2r7PLvj/a+Xz9lKIbjPos3Ds6uypIGJt1b3U7GYiq0ytXC+OIPoY4lkK3Wo0VKU9Xh/XDKeEwVT9EnrgUa5Rh3qQvfndnysIh4ToplytwK9h9KDv3TCTNiVOVE8WCWTjdto35O/J60EaborWitqZGVMt/NSn/qqujok6uYliJW6HcZev2jVsiBHIltmyUGQRAoMII9Ij6qNqLbvNZupykvrapk/dSJxLzRFp1oqnhuqILC+1vWCS7lJ7nSqOeOlRvYTNQB3YuVtm520NU/cIrJYrFAAkn27ZccdaYU2JzjdjUX9D9vO1bG+8tjLsmkI0J+OmTUwtzuctsZTG/QCAXQw/nggAIgIBvCPSK5vhAxJtUMVsdS6aJYy6WGaUmUzi3zJF6wtE60dJl43PkG17OGJq/+1Au3NNtU8OK2onu9DOCtMehtq1OzLYRw6nXDX+vbqjMHuSB1pM/dxbIfnFLXIMLKSsZGwiAAAiAQAUQWL1yOS3r+oz6uazDR9DGEzan0esUWfDVK+njZV3Uy4kOH05jNppAY4tOtEibPHX6alq+bBl91qdRpxGjNqbNx4/2lIVBMMaVth0EMC6XwR3u5b9mIJBdbjhIHgRAAARAAARAAARAwF8EIJD9VV+wFgRAAARAAARAAARAwGUCEMguA0byIAACIAACIAACIAAC/iIAgeyv+oK1IAACIAACIAACIAACLhOAQHYZMJIHARAAARAAARAAARDwFwEIZH/VF6wFARAAARAAARAAARBwmQAEssuAkTwIgAAIgAAIgAAIgIC/CEAg+6u+YC0IgAAIgAAIgAAIgIDLBCCQXQaM5EEABEAABEAABEAABPxFAALZX/UFa0EABEAABEAABEAABFwmAIHsMmAkDwIgAAIgAAIgAAIg4C8CEMj+qi9YCwIgAAIgAAIgAAIg4DIBCGSXASN5EAABEAABEAABEAABfxGAQPZXfcFaEAABEAABEAABEAABlwlAILsMGMmDAAiAAAiAAAiAAAj4iwAEsr/qC9aCAAiAAAiAAAiAAAi4TAAC2WXASB4EQAAEQAAEQMBdAqtXvEsL591Ljc+8Q129vTRq1ATacfIUOuGEo2ni2HUKynzlsjfooXvn0cLFb1GvlsIo2jk8hWacfCJN2nxkQWkG+6RldMNRs6h+KdH58xtp5sTCGLlRl4Vwh0AuhBrOAQEQAAEQAAEQ8ASBZc/cQFscfElGW2LNXXTu/uMz/m73wxv3nU+7nXSr3U/avupEK90yc1LG3yvxh+dvmEwHXLJYK3qstYfOnTQ6bwxu1GXeRgyeAIFcKDmcBwIgAAIgAAIgUFYCqz9eRLtNmEJtg1aEqmrokinb0msPzqJbG3XTQtTY2UpTNx+m78j6d8Urc2ijvc4zjglFauj8Y7elj5K30JXz9ZyIaqXwviJP4W0kGqgPq+n5ObPogPPmG6UqRCC7UZeGQQV8gEAuABpOCTKB1fTu8wvpXjk81PKvLlnQUTThR7vRlOOOoqMnT6TCBurcSDNodeACo9XL6fmFD9PDjUl6q2tggJTksGt4ynQ6+cSpVIkjpKUYuly55D761RVJrYFGrr+Npm1f2DBrcFq4C21bg7OSXllwH909P0n/ki4FvI2asBcdO+uEIu5VWjI++m81LTpf3p9vHRCtkVgzLTh3fxqQwavomRuOp4MvGVTJ0Qbqnztt8LdsRVxJfzlqFM3ST5M9xXOVnuIlsmc5pPcsh+PU+8yZVNEtfOX7NOdXR9N5/OIQChG1DdRF/gLZjbrMVs85/CaCsPX1iM6ODtHZ1eN6aXo6W0VjQ72or68XDY1J0drhfp6FFKqvp0t0dnaWhEnu9vWJLrYp07+uLtHT25d7ck4f2d8pYhES8rKx/xeJia5883QjzXxt8PrxLjDqaasX4Uz1OLg/1tTpdTKO2tfZVGffrnUezXm37nT7+tpEVOEuH5Lpx1TSHhfatoavu0VUhzLcp5h/uE50lPFWWrIq7mkWEb29hWpt7s/doi6sc4qIlt4cLOtvF9V6mlQzRJpVojWXNHPI1n+H9IqW+lohJfHAfSWlPeZ97btRl0VCpSLP98Tpva0x48afaHevtbbVR418dBFVlWgvO4P+njZRF62xXKitsfBgo40JzzyieluGFC0a13BUNLR2l5hrv0jWhJT6DYmaeL1IxKqVffJGUN0o+nO2zI00c87cJwe6wEjeaK3iOCxq4wlRn6gTkZSbeL2L9wsvVUB/V9J8kMkHmhyGli/5CVFteSEMicbO3Ft3evn6RGO1eg2RyPshmZ6oj/e40LaZRm+rqNJFifY3orXveF3K80neq4KukdVnfyTWattW2hJVxj28JpnDS7FFINeK9CdRr0gY102OotvWMp/vTH2eR6pFjcEl/2vflbosEnEwBHJb3LgAXLshy54R601p4EEQb3NPkOdSt30dDYNlj6QI5MjA/pCHBHJf6o1df7O3/xtrTr815cKkkGP6OxuNNkRUJZq6TKHQ15k0eynkA6khx64ZN9IspGxePscNRk21gy+HLASjCdFtVqVE0SMaa8zfKZIIvIgQ8pUuqQhXOQytvOT1iaa6wXsFi61og/Jbfi2nK1mrXEMD17Rr9+P8TCvL0W60bS5Is9K+qUq2b6V0fR2NysthSCSV+5hyWGA+tsVN8ZuprfUq+iCcQURbgagCWAq9lOdQb1vCbOdeer5aC+H+N6mJBnrvQ6KuoUW7j3YoLyOZ6iOTYe7UZabcctsPgZwbJ/nW3mKIpKpYy+BDxPLkzTUlR48zL36rQO5qToiamhoRa2gt+IHnqKGcmCKQwzWNokO6WnRI15iBf+2itaVJxKsV8ULVoqNEiFtipkiobVIfOQMUupvN4elMPRWpvNxIMzUPv393npEcUjV6iTMNf3aIGq3njUVcVLQHvZutFEOX3U0DwsxgP9CBkO9D0u/tWbXf+bYtU+9XO2qqRJtN2zVGD2Ubrwu4i4sqqhIZOqv62usNQZvrvbuzsWbgnMH2XB1vFG0d7aJJuhRoo5yD+6sSbWqVV9znHsmkW2mDan3ke+2r5zpZl8VUCgRyjvT62823xkR7iVRbDraZdsmbpXfMsrdcEciReKYbS7/s4dOHacMi5eXdPt2i9/aI+FB+auoIgvR1G3qgzo00iy6oxxJwgZEcfjZ9EmPCfnynT9RX6aMWwR8idX/oUtajMbQaFlUR8yU334ekxxpoEea40LalNV1NZi99Rve+ng7R3Nwi2to7RI8iXooojGdPNUWVfBnOVFbl3p2rQOYCdzamuNcZL9UD945wxmeYZ3G5bphZH/m7WJjnOl+XhRbcGYHc1yHitTWiprZedPb2iGb29QuHRCjE/8KiOtYougYbb1tjTPktJKpqEqLD7inW3y3f1uq0m+1AOiERjkRFrLEl7aFn9qLaVYp0JG+IiSrDHj2d1tyGVmXZErW1oqba7GGMRGtFnSxvPNkhutsaRa3sqU00yx7QhloRHixzVU1ctPcMKNa+rjZRH6u1liUcEdGamGhqT++t1CpTlr9Z2h2VDxu1/Ilk26Ddcmg0XidqorpdIRGtrZO21IqkdAHobJI9yNLG2nhTejnzYCuMuk2Irv4+zSmfyyhnq2p1W1UdE825TlRUBXKWoa52ZZimJC4sil0Ujmfw2e5VREAOosqNNAu9yr16nluM+vtFr7wPdXfb3VgkDOljaE4kqynZKEW5qsF88NjdHwesUu+huQ1Dm6VRfTyrGztEuzJXo2IFskttu1UZ6WoYfEvv6eqQo28tokX+a23vTL/fm1UVuE/tCd3vOiSaMk22UeoiV4Hc39Usqo1OE/1lOuVvqFo0B9yFJd8Gk8u9JlOabtVlpvxy2e+MQFZ7bVLesvTJbBSplSJaF3MpDS1lmDPV59NIQ087JCekKReDenO33JDl5LUaY8gvNU/5PVw79PCqvLisE37MdEJ1zyg9j+Z+3d6EHLvtTJpD8/r+1L+1KRMH+uVwpdELppdZ/StnKHf294pYhrLVtfQI40Yatvog58uWJ4RktWXQrrjMc8hNvVHF7SdUcBqmD6nVbWTI9As9QLGLffrsZVWfaIjqdZyDXW6kWWj5vHpemRi1xpX7UAX4IKsPLaeHLs05EPLaiMQ1cabmZ7kfe7UdumGXS23bZBsVze0totboudfvTfy3SjS0Zeh4caOsZUzT5JGl00Kpi5wEsuxxNl+guV3Xyk6gbtEnO4i6O1pEnTH6NMA6g2dHGamUL2uzPjK/jGeyzjzXwbrMlFmO+50RyEoDHBB/Een7mhTNybiNuJIzymNxEU/ELW9oVfXtAyZbend4tnWtaGptF20tjZbjKVRnTE6wF8iqL+JAI0+2ton21iZRqzZw+YC0F0QmwU55jhr+K1pXLxobG0Sy9T1lNitfLPJfuGpwpry0L2U2fU28Qb7hy7LI9Oqi5jAkl8UMsJRit17+5gYRVQRxtEEOn8mQczGjLNJRvr5RhqCTecjueqOxyR5Ro3wFsFX9hgfqNizqEjLEnQx1V1ulu0JwuTP1vJoc1bTCtUnR1S1D0cnQbl3yX2en7HlqbRbxGkW8yAlDmUbNlFSL/6i8BGR2/RDC7CnLQSC7kWbxJfVWCmVg1JUS6iyTYPQWqOKsMe4FUjg5OwzdqfhyR0Tz4DuymV/+D8niSuqhs11p272Ka9Dg80btOEn5XNdkPlU8RMZRU8y2Zra/tAy6zag2uQjkjgbFtUK+9KV3/ch6MDpLSBjaJS3jytth1kf+1755rnN1WWwNuCCQqyyxBvsU312isEiqYYQUAak33A5leC5c25QywaxHNkxTlNUO3gDsBHJPi9lzG5ITwqxCq08klZnAuQzj93eYjv5xY2aEdbYrT94b2PpkPN9+0dGgD/+Q0G01K0z62hozy803ps7k4OQAebNLs9sicAfCz/R36L7RVh9ko7EpArkQtqqo5Z4Ja0dxj0gYAt0sg1nGlE9pL1LZbvJR5aUhJR2nvyo9BqGa5oypG0wpB4HsRpoZLfPpDyVm1N1iRrvhlz2+v1TC5tbQpTnSQ6ImaYox8zrJ/yEZmPpwpW2rbl76vTMsXf1aZWdMj+hqbxI1FreALC9EAQHdpowGxTIEJFb1QS7uQ8boq7xH1GeawatPSuWXkhw62QKCe8hiFHPtu1GXQxo8xAGOC+RI6tC5vFHo4dHCtaniwxSYAwJZfjcEV9R+0pkiqkODDzj1AhgY0lPFp7xJ2E1e6zNj8uZy0aTnwWRN+8lGNPV0DCwqEovV24i9fmHOcjYFl9lI7N+i2qWfc7RauqvUyx5YWS7TLjMNtsxoqIZALoytKpDtJoUY+diUn+2wbHkJZPlmXmfjP21J0KEvil36i5pdyoWW1bE07Yzy8z43uGfg0dVkxkrXRkKi9ebISoZzgrJbbbcZF0rIsS50Jj0tCs+U2OBmfpUskM2Qls5d/+rzhgVyRIaj1GtE/9ttGe0MepQFtdMnU4xjNfyg+iKnE7P+VRln82s2dU1Oo6fWTAL7rZhr3/m6LB6z4wI57S1OvfGmimdFYOoC2ZgNnXF4XWnAg/61pkjUb8jWN+1ItFpEo1Hln/yu+G5lu4HpiNPz4F8UW+RQjOHKoJ9k/JW+yG0tIindMhIxnlhXZQnab4prZQgta3pGwnkJ5ELYqgLZrqfdfFBaBbppofJJaQvpYd46pOtJs2iI11jYlGT4SrWrLvUlzrS/2YgXm2dZnUrTNCUYn9zgnkZGvogaE3kGet1C1Q1ZrtW0BHy/w3xo2b90awXMZxhaug/onR48qpTacdeaQ2xa30MdqgCutG3rcy2quyWm2KKO2ubybEs53VdfLbGmU17U9IKoMcDrc4hhb14vJOyeeVq6PYNhDbkHOaNW0S2onL8qu3znH7hRl8WSd0Egp3jsKDeK9IvVFJgDv8m338EholCt7q6QWkTzHJ4UwqI0Xbwqx3ADHupfDsG+0/Ngu5R8jJ5aq71tssd3yPyN3lflBpghPWvqatmtos1oqEY6hbFVBbJdgze5WPNPtVP7rraFLCFy+tobFJFst3yobeqF71T8Bbk3wP5FR6kbWV8Ze+J0K9xIU087KH9dZyRdsgw3poH7QKQumeJuFRSYmcthjkpxB0KG1p3HYgpq2Di+t4WUuRGZ7nVpI4uZzQ3GLy61bXX4vyZTDExl1Db4vZtdStzzkHSJsLZvjoFsLoWc8iyRk+56e3sH/vWZw8xqFBaKxIy5TmbDlBO2lftKtnkr5jmV8cnQHfK+YKcXdAp9OvfePsWNtoi61BN2+K/HBLIZTzNUk8k/0CpKWY6bIk2vFOUYWVGJZJNIJpNp/5qamkRTk9wvQ7RZfZTTKafnwcco+dgIKzVmpfbgCMnQbtI9IpZoEC3tHUq8X11cKiLM8R7kwti6JpCzhHmTK4ookx9zEKPp1ZXfHtW3O2OM4y5RqwuBjMco2bqRppJ8ID66yqhbxA13rQFxXNMwOBE4EPByL4TTQ5epAjmTKFb35+LGlnuJfHCkS21bjcBSm4NADtUkFQHiA24FmKjO9SEKiXhzh+jt6xUdcrEsQxxLHVDd2GlJXW3H4TolqpKsu2p5vNF+IzWiqa1TpqlHsTDnQfHor3VejiWLivuSm0CWOsfwlQ9bOpsKrUu3QHtMICsCUYqQNPcqptDfYTbeqsTQPciZ0pG3jc62Vi2YerecUDfUlr9AVsrCF21LemnMeL+6QFaXhK2xXYyiu3nA9y8UrtFWUTLtsk7IMBqqIdwVezIxsWFbHoGs2GozhDtUXeX/u+qzLpeSVieS6ol1KUtRV+USXcONNHVjgvLXLUY8mVd5wPFLcktlhL2yaxlOD132dTbLOPB1IhaL2f6rjpgCIlItj6urE4kmqzixszNY+9xp26o/rT4HJ5Vbb6s5GTV91Db16CB8T7/eDXGrC13Z4ZQytm3pWEvl1Kv2POtp2PyNVfB9xa7lqC9wmXuQ1ed7agdYYXVpZ4sT+zwmkPuVGLhymUybN2Q1BIvun2qKRL0HWQhTfJKw89XqbjZdH0Lq22MGqnZ5ZO9BtvYup/VQy2Ew8y1VF8jCEvkifUJBv2gwesUGBLFpV0ioL8jpArkwtq4J5CwuFp1Js24oJY5zhuoperfaHihtApd1SC01Ion9cJEQxaRZdIF8kkAxjDJxtwyRyh4eS+Qcn3Bx1swihi4zDENns0+995oRf7KdEczfimnbIhN3tWdaCrZUlwK51p7hpsgi0e4ZGkzavaI5roRnU8RsdSyZJo6ZQV+bHgHKXiP0y3UUYsoCYaroDlXViRZ99bNgAi2oVGoUrkSKu4uZoNRGho6RwRjSxFH+dWmm7ewnjwlkWbiupDm0wRd44+DKcf09chU3MwSaOrRhikRTIAsl2gU37OpEsxhY2K5PG3oxF/9gYelSD7IxjDAw7DOQS78MNt6cEo5HeYvqbbHEjq5LDrp/9HWLZMwMG0eDQ2eW3gK5kmFrG6+N3m8TxaIwtm4JZJKrENXLSYv19fXGv0QiJqqrlPjQXG+lGhaXvedqcPhQVK7w2CP90+SyrQnF34wotWdfvg0b9WwdLuLRjsLSdPYi93RqBTPKwF36fpoTyAZ6kWvrakV1tVzpU654af0nJ+vKHs5MkZw8zS1P4wodusw4DJ0lf+PlXF6/mXuRsiQQlJ8Kbtuy66XVjBJiGf6XbFSfcnYpiDXKMG/Sp7O7M2XhELmgVPq4ZVDg2pejv7dbdMi1Btr5X0enI0tt96lpStfIrqCv322PtuR73ajLfAvhmEDWV1tLuyEqkxVShzHUHlj1t3Y1ULe8yapvbvrnumbz0rcVyJKEpScyQzrhLBEGVJjqDcsso7WXOHUIp7NRFfSyHCG5PHMGO2KKI9PQdkeNmeP9nQ1pfNg3zXhISRcL1a582bJAzli3EpDJ3uwFV7lZPittQa/HbH9LHW2gR+lRyGRXXF3CUStctuEiIQpL00It8F8KY2TPXb1OM9WhdX/KS01gaRc2dGle3yTUe3Q2TLkNs2ZLITi/Fda21fuqHfceyyQxa3vWn5dyzQEsgxychoSSlIWAQwJZjwkYSg+s3S9XWxqc3JQ+k9kUmKm/dbc1WlaO028CIekwn2xXJZ/1ZpIqYHpl8HTbNdXlhLm47J0duu94sF6UwOBmHqb9IRliJm2kQKbe1lBnK4qjcjZ9V1eL0cOY+vDpaZflN3om9ZueXNygOi5SRy5aEgNDS+HIwCp0PCHGWPXNJgRNPmzlONRgj5xN3Uo05jBVerintBYte1T0tqDXZ+rfUJgnMtaJxpbOtNNLsaOvM0N7CVentbsBe4YaLpKM8k6zFCX1Vh75M7LnnjYxNsMLqdnuqkV7zjcBbzHL35r8hy7N69t+GNrOBrVjwLxX2h1ZGfvyb9vqfTUT98zPlnAUw/+V0bJQSrcJrMEZyIeFZ7cVHy+jnj6iYcOI1h21MY0dvU5Btq5c/jF19/bJdGRCw0fRhPGjSX4qzbZ6JX3c1U39nOPwdWnjcWNpnRwzt5R/I1n+kRnKv2oVreKy9ckyjhyZU9ksaRfBtjQQS5nLalq+bBl91tevZTpCstlctpfiNjfSLM4i750NRqWok9Url9Oyrs/k/Uhuw0fQxhM2pwJvq6UwNyB5uNS2+dmyrIt6uTKHD6cxG00o+BkZENAoBgg4RsDzAtmxkiIhEAABEAABEAABEAABEMiBAARyDpBwCAiAAAiAAAiAAAiAQOUQgECunLpGSUEABEAABEAABEAABHIgAIGcAyQcAgIgAAIgAAIgAAIgUDkEIJArp65RUhAAARAAARAAARAAgRwIQCDnAAmHgAAIgAAIgAAIgAAIVA4BCOTKqWuUFARAAARAAARAAARAIAcCEMg5QMIhIAACIAACIAACIAAClUPg/wPB8ihNVRUR0gAAAABJRU5ErkJggg== />"
Question 4Clumsy researcher that he was, later that day he spilled a little baking soda (NaHCO3) into the beaker. He figured if a little sand didnt hurt, then a little baking soda shouldnt matter either when recording his melting point. Is this a valid assumption? Explain.
 Question 5
Question 5fJvKIEHfxeOIoAAAggggAACtgCBB1uDfQQQQCBYAQIPwXrHvDYCDzEnpUAEEEAAAQQQSEABAg8JeFPpEgIIxI0AgYe4uVX+DSXw4O/CUQQQQAABBBBAwBYg8GBrsI8AAggEK0DgIVjvmNdG4CHmpBSIAAIIIIAAAgkoQOAhAW8qXUIAgbgRIPAQN7fKv6EEHvxdOIoAAggggAACCNgCBB5sDfYRQACBYAUIPATrHfPaCDzEnJQCEUAAAQQQQCABBQg8JOBNpUsIIBA3AgQe4uZW+TeUwIO/C0cRQAABBBBAAAFbgMCDrcE+AgggEKwAgYdgvWNeG4GHmJNSIAIIIIAAAggkoACBhwS8qXQJAQTiRoDAQ9zcKv+GEnjwd+EoAggggAACCCBgCxB4sDXYRwABBIIVIPAQrHfMayPwEHNSCkQAAQQQQACBBBQg8JCAN5UuIYBA3AgQeIibW+XfUAIP/i4cRQABBBBAAAEEbAECD7YG+wgggECwAgQegvWOeW0EHmJOSoEIIIAAAgggkIACBB4S8KbSJQQQiBsBAg9xc6v8G0rgwd+FowgggAACCCCAgC1A4MHWYB8BBBAIVoDAQ7DeMa+NwEPMSSkQAQQQQAABBBJQgMBDAt5UuoQAAnEjQOAhbm6Vf0MJPPi7cBQBBBBAAAEEELAFCDzYGuwjgAACwQoQeAjWO+a1EXiIOSkFIoAAAggggEACChB4SMCbSpcQQCBuBAg8xM2t8m8ogQd/F44igAACCCCAAAK2AIEHW4N9BBBAIFgBAg/Bese8NgIPMSelQAQQQAABBBBIQAECDwl4U+kSAgjEjQCBh7i5Vf4NJfDg78JRBBBAAAEEEEDAFiDwYGuwjwACCAQrQOAhWO+Y10bgIeakFIgAAggggAACCShA4CEBbypdQgCBuBEg8BA3t8q/oQQe/F04igACCCCAAAII2AIEHmwN9hFAAIFgBQg8BOsd89oIPMSclAIRQAABBBBAIAEFCDwk4E2lSwggEDcCBB7i5lb5N5TAg78LRxFAAAEEEEAAAVuAwIOtwT4CCCAQrACBh2C9Y14bgYeYk1IgAggggAACCCSgAIGHBLypdAkBBOJGgMBD3Nwq/4YSePB34SgCCCCAAAIIIGALEHiwNdhHAAEEghUg8BCsd8xrI/AQc1IKRAABBBBAAIEEFCDwkIA3lS4hgEDcCBB4iJtb5d9QAg/+LhxFAAEEEEAAAQRsAQIPtgb7CCCAQLACBB6C9Y5JbR9//LGsXLlSHn30UVm9erXU1dXJ0UcfLd26dZPU1FSZNm2aXHbZZdKxY8eY1EchCCCAAAIIIIBAvAns3btXVq1aZX4vvfTSS7J7927p1KmTdOnSRS6++GK54YYbZOTIkaIBCTYEEEAAgbYVIPDQtr4xKf2zzz6Tf/3rX+aL889//rNs3LhR