|
|
|
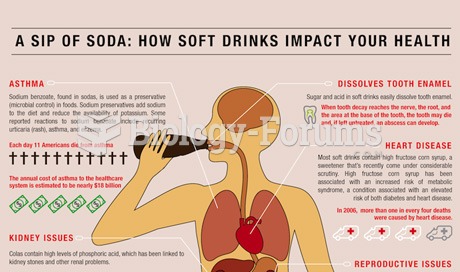
Human stomach acid is strong enough to dissolve small pieces of metal such as razor blades or staples.
The toxic levels for lithium carbonate are close to the therapeutic levels. Signs of toxicity include fine hand tremor, polyuria, mild thirst, nausea, general discomfort, diarrhea, vomiting, drowsiness, muscular weakness, lack of coordination, ataxia, giddiness, tinnitus, and blurred vision.
According to the American College of Allergy, Asthma & Immunology, more than 50 million Americans have some kind of food allergy. Food allergies affect between 4 and 6% of children, and 4% of adults, according to the CDC. The most common food allergies include shellfish, peanuts, walnuts, fish, eggs, milk, and soy.
Ether was used widely for surgeries but became less popular because of its flammability and its tendency to cause vomiting. In England, it was quickly replaced by chloroform, but this agent caused many deaths and lost popularity.
In inpatient settings, adverse drug events account for an estimated one in three of all hospital adverse events. They affect approximately 2 million hospital stays every year, and prolong hospital stays by between one and five days.