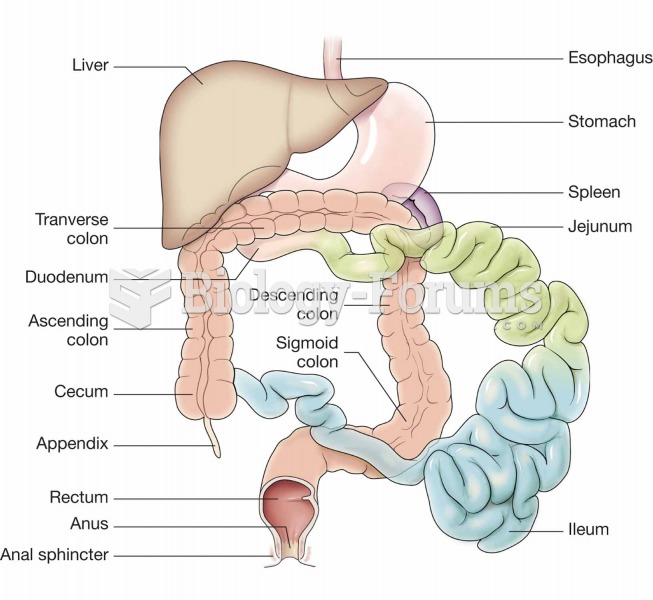
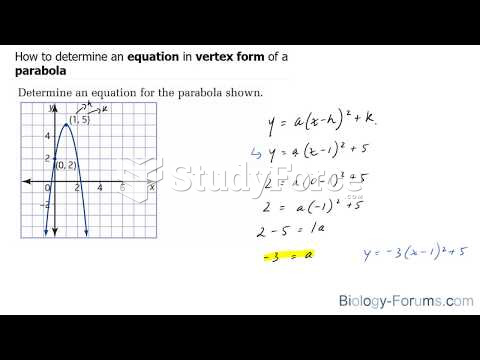
|
|
|
In 2010, opiate painkllers, such as morphine, OxyContin®, and Vicodin®, were tied to almost 60% of drug overdose deaths.
If you could remove all of your skin, it would weigh up to 5 pounds.
Sildenafil (Viagra®) has two actions that may be of consequence in patients with heart disease. It can lower the blood pressure, and it can interact with nitrates. It should never be used in patients who are taking nitrates.
Not getting enough sleep can greatly weaken the immune system. Lack of sleep makes you more likely to catch a cold, or more difficult to fight off an infection.
The effects of organophosphate poisoning are referred to by using the abbreviations “SLUD” or “SLUDGE,” It stands for: salivation, lacrimation, urination, defecation, GI upset, and emesis.