|
|
|
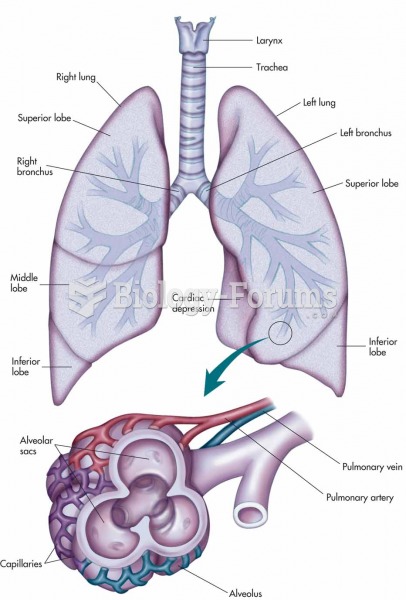
When blood is deoxygenated and flowing back to the heart through the veins, it is dark reddish-blue in color. Blood in the arteries that is oxygenated and flowing out to the body is bright red. Whereas arterial blood comes out in spurts, venous blood flows.
Certain chemicals, after ingestion, can be converted by the body into cyanide. Most of these chemicals have been removed from the market, but some old nail polish remover, solvents, and plastics manufacturing solutions can contain these substances.
GI conditions that will keep you out of the U.S. armed services include ulcers, varices, fistulas, esophagitis, gastritis, congenital abnormalities, inflammatory bowel disease, enteritis, colitis, proctitis, duodenal diverticula, malabsorption syndromes, hepatitis, cirrhosis, cysts, abscesses, pancreatitis, polyps, certain hemorrhoids, splenomegaly, hernias, recent abdominal surgery, GI bypass or stomach stapling, and artificial GI openings.
Signs and symptoms of a drug overdose include losing consciousness, fever or sweating, breathing problems, abnormal pulse, and changes in skin color.
Thyroid conditions cause a higher risk of fibromyalgia and chronic fatigue syndrome.