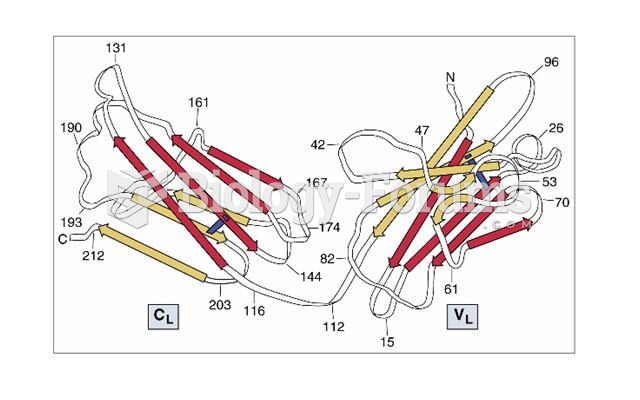
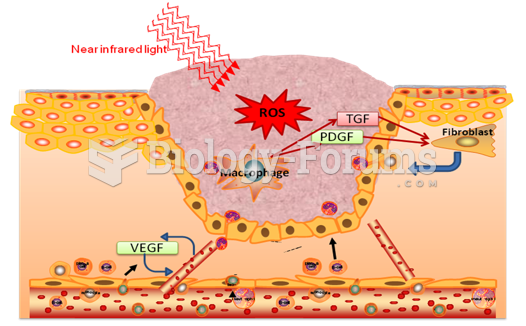
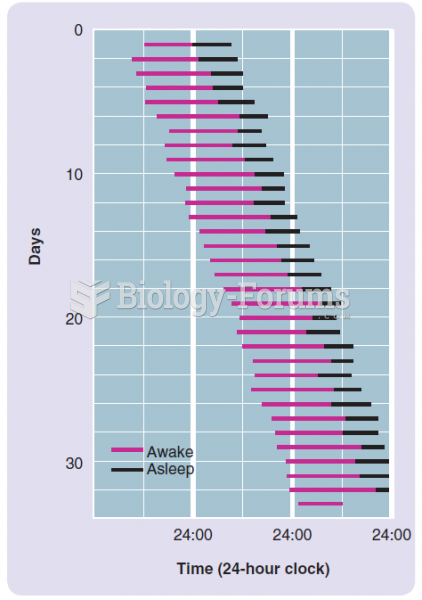
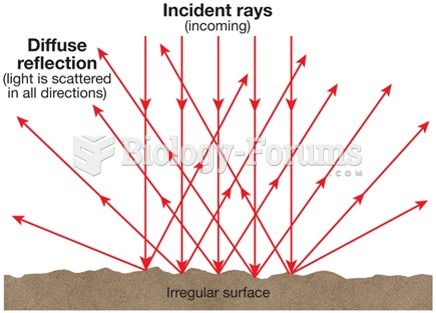
This topic contains a solution. Click here to go to the answer
|
|
|
Did you know?
When blood is exposed to air, it clots. Heparin allows the blood to come in direct contact with air without clotting.
Did you know?
Vaccines prevent between 2.5 and 4 million deaths every year.
Did you know?
Drug-induced pharmacodynamic effects manifested in older adults include drug-induced renal toxicity, which can be a major factor when these adults are experiencing other kidney problems.
Did you know?
The first documented use of surgical anesthesia in the United States was in Connecticut in 1844.
Did you know?
Most childhood vaccines are 90–99% effective in preventing disease. Side effects are rarely serious.