|
|
|
People with alcoholism are at a much greater risk of malnutrition than are other people and usually exhibit low levels of most vitamins (especially folic acid). This is because alcohol often takes the place of 50% of their daily intake of calories, with little nutritional value contained in it.
Asthma cases in Americans are about 75% higher today than they were in 1980.
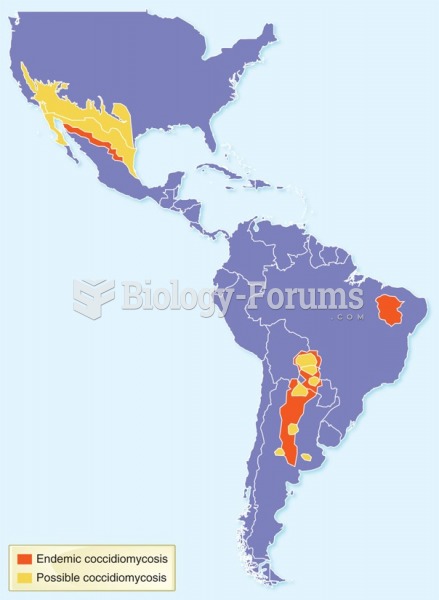
As many as 20% of Americans have been infected by the fungus known as Histoplasmosis. While most people are asymptomatic or only have slight symptoms, infection can progress to a rapid and potentially fatal superinfection.
Pubic lice (crabs) are usually spread through sexual contact. You cannot catch them by using a public toilet.
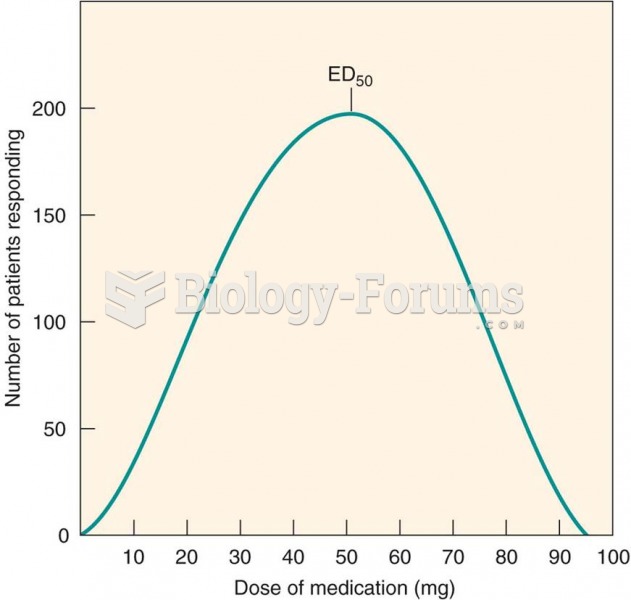
The FDA recognizes 118 routes of administration.