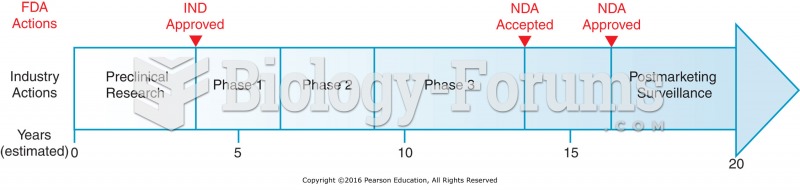
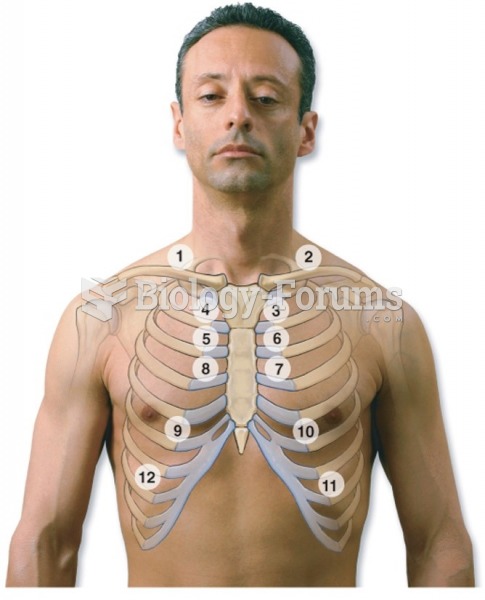
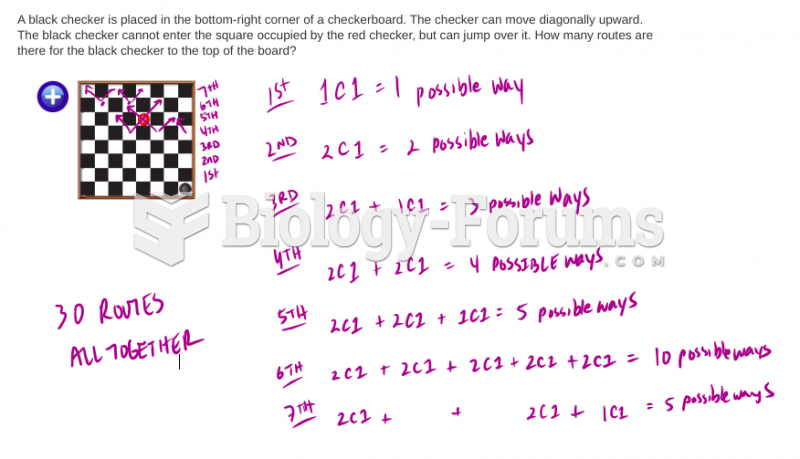
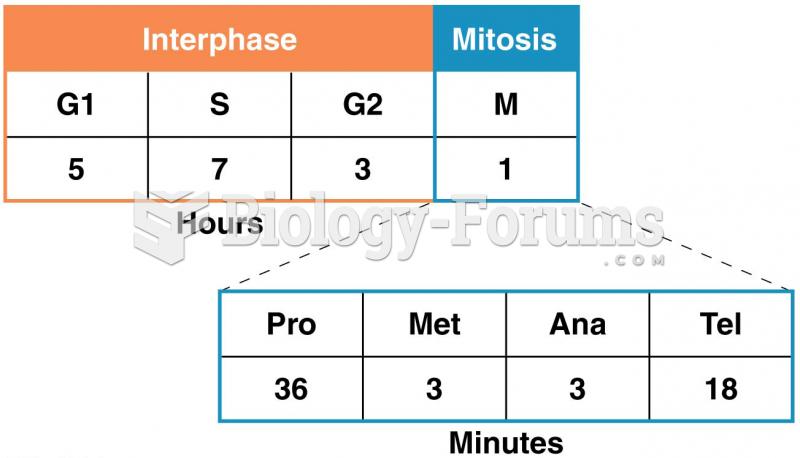
|
|
|
On average, the stomach produces 2 L of hydrochloric acid per day.
The Food and Drug Administration has approved Risperdal, an adult antipsychotic drug, for the symptomatic treatment of irritability in children and adolescents with autism. The approval is the first for the use of a drug to treat behaviors associated with autism in children. These behaviors are included under the general heading of irritability and include aggression, deliberate self-injury, and temper tantrums.
There can actually be a 25-hour time difference between certain locations in the world. The International Date Line passes between the islands of Samoa and American Samoa. It is not a straight line, but "zig-zags" around various island chains. Therefore, Samoa and nearby islands have one date, while American Samoa and nearby islands are one day behind. Daylight saving time is used in some islands, but not in others—further shifting the hours out of sync with natural time.
The eye muscles are the most active muscles in the whole body. The external muscles that move the eyes are the strongest muscles in the human body for the job they have to do. They are 100 times more powerful than they need to be.
Tobacco depletes the body of vitamins A, C, and E, which can result in any of the following: dry hair, dry skin, dry eyes, poor growth, night blindness, abscesses, insomnia, fatigue, reproductive system problems, sinusitis, pneumonia, frequent respiratory problems, skin disorders, weight loss, rickets, osteomalacia, nervousness, muscle spasms, leg cramps, extremity numbness, bone malformations, decayed teeth, difficulty in walking, irritability, restlessness, profuse sweating, increased uric acid (gout), joint damage, damaged red blood cells, destruction of nerves, infertility, miscarriage, and many types of cancer.