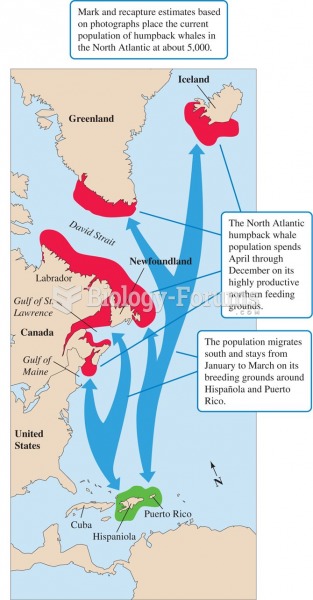
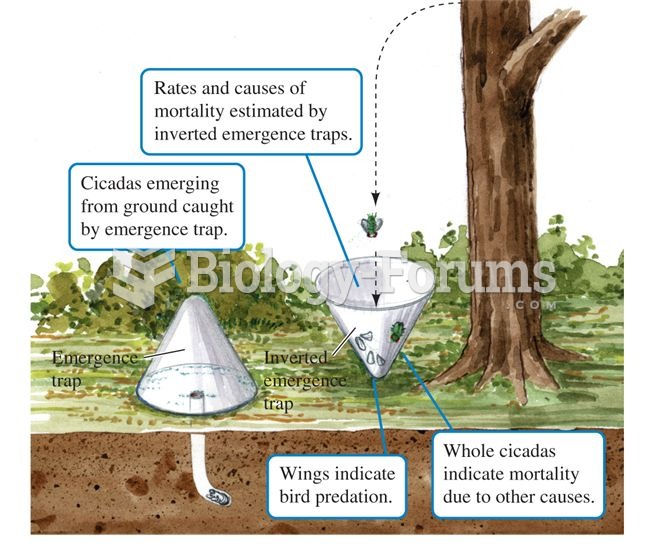
|
|
|
Certain rare plants containing cyanide include apricot pits and a type of potato called cassava. Fortunately, only chronic or massive ingestion of any of these plants can lead to serious poisoning.
Disorders that may affect pharmacodynamics include genetic mutations, malnutrition, thyrotoxicosis, myasthenia gravis, Parkinson's disease, and certain forms of insulin-resistant diabetes mellitus.
The Centers for Disease Control and Prevention has released reports detailing the deaths of infants (younger than 1 year of age) who died after being given cold and cough medications. This underscores the importance of educating parents that children younger than 2 years of age should never be given over-the-counter cold and cough medications without consulting their physicians.
In most cases, kidneys can recover from almost complete loss of function, such as in acute kidney (renal) failure.
Immunoglobulin injections may give short-term protection against, or reduce severity of certain diseases. They help people who have an inherited problem making their own antibodies, or those who are having certain types of cancer treatments.