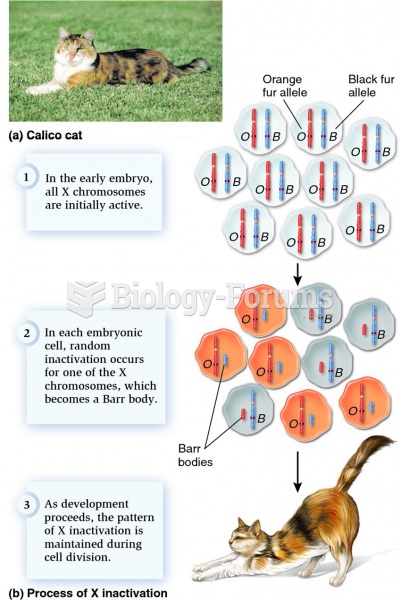
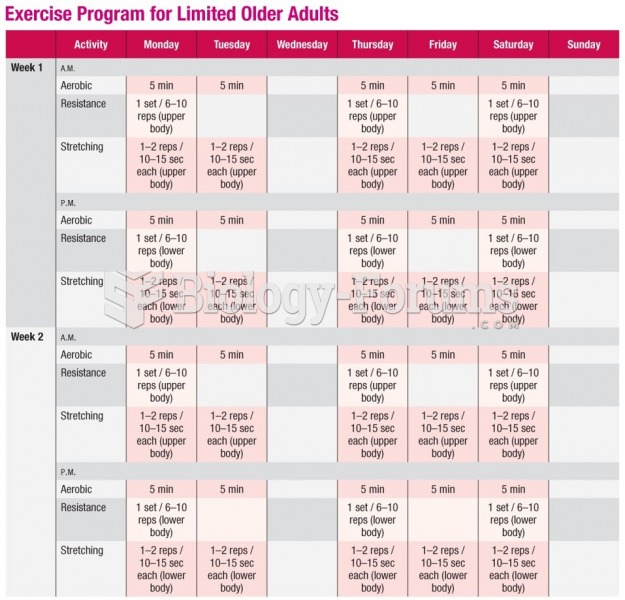
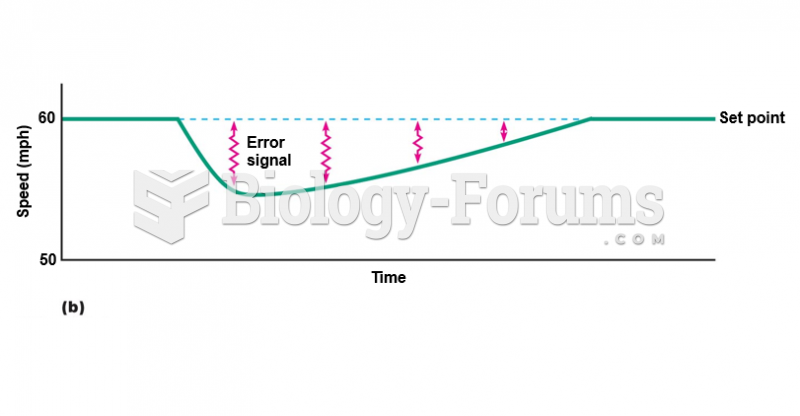
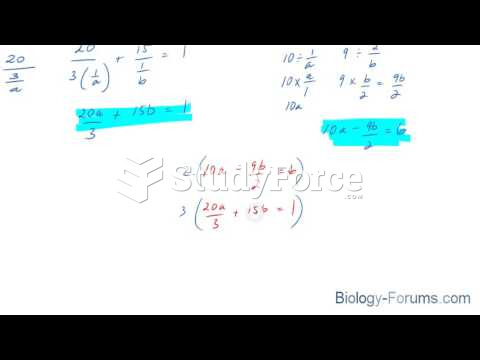- Grade 11 and 12 Mathematics (Moderator: geoffrey)
|
|
|
- Grade 11 and 12 Mathematics (Moderator: geoffrey)
As many as 20% of Americans have been infected by the fungus known as Histoplasmosis. While most people are asymptomatic or only have slight symptoms, infection can progress to a rapid and potentially fatal superinfection.
Many medications that are used to treat infertility are injected subcutaneously. This is easy to do using the anterior abdomen as the site of injection but avoiding the area directly around the belly button.
Cucumber slices relieve headaches by tightening blood vessels, reducing blood flow to the area, and relieving pressure.
If you could remove all of your skin, it would weigh up to 5 pounds.
Street names for barbiturates include reds, red devils, yellow jackets, blue heavens, Christmas trees, and rainbows. They are commonly referred to as downers.