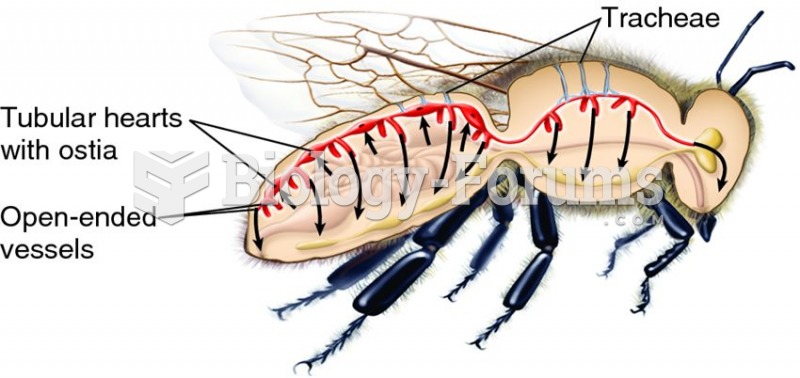
Suppose XL > XC in the figure below and, with both switches open, a piece of iron is slipped into the inductor. During this process, what happens to the brightness of the bulb?
 Question 2
Question 2n/IArDaDuCn5KEU1o19ls657Ev5c1mYIsJs5gNK3NkOtb4DcJxYNZy6idOceDFw8n2UupwX01mdbZ/YNShZedfoMSvd9AtnpgOr2Im/t2+j39EqIJtpsRspCa98Ww1xH9E9nhas3g7KNW+Od8Jy9iOJ3d2PAygWgvLSt1W42DH7KEegyBMJA4K3LqmsUpVBEytBBSPnhIIz9/tdRfS4PxUdOoOT0WVReuoK8CyVoPFCPxsZSyCaJJT+VLA7EJiUgZXg2Bi8eiMx7RyBt5B2IDUQxY5qWauSooy3+/MfUOv4971MjAau3qByAbNeBAAAgAElEQVQl770PMcYCWZWhCSpK31iP/gvnQhNEiG0QOPseBG7kpWs2Q62qhDkxEaLNioajR1G97zBSHpnMFiSN5F3XIURJyUH7CkTU5+aicsduyA4HRFWELOgoXL0GfZfNhxh82ryuOn/LEegOBCJG4OTGxezjOmWM02GSTEgdPoi9RgdGqnj9eOOPf8B3nnsO48aNxfoNa+FMTIRsNUG8LpMz6U2kGjHXctHIZs/puzu+MpHpM6hXF2x9B42F+ZBjEgBNgRDjxLX9h1Hz+UkkjhoNnRmiW5OBUlwB/rprKH57B0SnAxoogZ4IwePBlTUbGYE3e168oRFSDugo2rId9aXlsMc5IXpVKE4nrh06iurjx5E89p5AKf6PI9D9CLRiTQyTUAL9VEhjoifW1vVk2WKC7nSgXlPRKMuIy8qE2W67gbxJIhKUtWWscTbFPQyTtLyZKEDAr/hRvHYzTIIEkyBAsZlh1jX46mqRv3orM22QYtDWQVcK39uNhi8uw2SSIJvMEM0SZLsNFTs/RH3u5dbM503NiQK5p7qRv2E7LCZSEnSoiTGg3bxqTT0zqzQV5iccgShAIHIEHurgAgHcJV2HyhJghlqRl+tNCBD5Xjt0BK7DJ6BZLDBlpeCuf/ke/KIG2WZF6ZadcFeWsYTWNxt3wVubIGsqfA2NGPB/nkafiRPgURXoRWUoWLP1JlUN3bx870G4j55mphJTvxzc+e/fh1dUYLLLhgwV5Tdpg1/iCHQtAt1P4F07Xt5bBxAg74ygi2bwfweaab0K7bhkujVQ9NYmeBQvFHcjUidOwIBvfQ0xg+5kGcsbr1xExdadLdY8aH8uyRPMU111/DRqPzoG1W6CJT4emc98BdlL5zI3V9VmQemG7fC53UwOCrUQ6LZJLjLTFazaAlVxwe3xI33KFAz8u5WIHToEXiioz7uKss07jfqa1pRJPdgABXpjsbOYvS/4aXj+B+cg7PiHRzzeSjchwAm8m4DvSd1GjDzoqYsxnoD6gmIUv7cHZqsdZpsV6Ytms6zlmYtnQ/UokGQdeWveDricGushTC7aHcnaIM+RTfDW1wIuN/pMmYCY5CQkT3kI8QP6wgSg5vRJlL+/x4Ce8XdLpq29nIuq9/dCsskwOZzIWjSDle2/ZB4klwZZBnLXbIGmUgZ1emZoWV/QVcPsItItKWhRD99Mc/IOH5a9pSVO4L1lJiM4jqDdmf4Hz8PSnSBAkmS2jatsy1Z4C0qge91w3DseiRPuZV1kLpoFe3oWdJMV1Qc/w7VDhwNd07InuZCKEEUBvopKlG3dDskqQpfMSF+5lJWzJCQidf4C+NyNgGZ4tBDtksvi9Sp46bqt8JWVQvEJSHroASSOpaBoQPrCObBnZEMyCaj7+AiqPvqY+ZKzBfWgNCz4FlnLNUjMat62rT5QpV3/wo59u3rnhaMVgYh5oUTrgLlcHUOAIvvt3LkTb731Fux2e8caub4Wue5pAMWumbz3GGxOKzwuF4YumQtZNsMPwN5vAFJnTEbuX/7GCDd31SYkTXiAEatI5hPBcP2jxcv6y/mglHrxI0YhfepDLBI8kXzGioW49Ic/Q/X6UPrhx6g7fQ5xw++EShvAKDiaKLDAWSUbtwE2GX5NR86yuRBEmfXjyM5C4uzJyP3j6zCrCgpWvY2khycyf3LSs1nCE0FA+f6DuPh/f4VrqUnY5RDgbn3P0fUotPqeCDuocXs8HgwfPhzPP/98eG+grfbMP+xJCHAC70mz1U2yBrXuU6dO4Y033gi7FGkAHrWmQ5d1OLJzkDlnKiNOMnvQkfnkfBSuWQ8dPpS8uxeuHxbCnJkFMlmQHk2RC/PXboZMJfxeZC6eCbnZTSZhxFCkTLoP5Vv2wNvoQvG6rYgffifbp6ApGiRRQvHu/ag+ew4WmJDULxvps6axvoM+4xnL56L4jQ0QBA0lOz7EkPwCOHKymQmIZFAVP8786y9R+dFeiJCwGtdQYYgflr+TJk3CCy+8EJa2eCO9BwFO4L1nLiM+EqvVymJs9+/fH4888gjrL6gldrRzRQDS/TqkfZ/Cc+kyhn53MRzpGcbCZMAKkfTg/Ui4ZywqjxyEnleA4o3bMei5p6HCCOVQ/dkR1H70GWSzCUJcItIWzW4hDjWTtWIZSrd9CJNZQMnGdzDgu9+AJT4RmmxYq8vf2ADR54dL96HfnJkg00vwIC075YH7kXjvOJR9fBBSQQFK12/FoOefgUQXRQGVhw7D9dlnsMbGQHDG4e9mLka1ZPims2G00yRON0166jlz5gwOHjyImJiYoDj8P0egCQFO4E1Q8JNQEKAsN9nZ2fjd734XSvGQy9RcvAz3lTwkTXqQeXI0d/dmm8CWzUXZ4QOQbBLy12zDgP/zd4DZxJYK89dsgdJQC1USkD1tNuIG9m8RQ5y4M236FMQNG4yai2dQc/EcKrftQtaTSyEJAmq++AJlez+EaJNhNVuQuWJeS7k1QJYtyFw+B2UffQTFpqNo3Tvo++zXIVos7Ckgf9UWuHxuCD4ZA5Y8jp//4ect2+jgu1dffRX79u3rYG1erbcj0O2LmMHH8+Y2P+ZdEHBd4+eGq1x340A/hKC2HUxVFs4fR/zggUifPgVmq5k5eDRfAiQCzpw/A3FZGdAlGQ0njqPsw0Ns8dNdXoqSd3fDbLVCMZuRtXThDWKRk4rZaUfK4scguhUIko68tesNlz8AxWu2wlNZCcWnInn8w4gfNbxFG5pA1nggdf4M2AfksJgq106dQeWegywuS0NBESq2vw/ZboXZakO/J26UoUWD7Xjj9XqbSgfx7+7vQjj7p8EFx9U0UH4SMgLdTuBBSelx0WKxsLdE5vwVXRjQxATnJzhnXfWfCNyZnorkx2dCbPCzDV/5b65l3Ze8+wH8F/KZL3nKsOFImjqeLX6yJFABAckzhNrIWTwPtj7p0E0WVBw4jpqTp6ErfhRu3g7RaoWkikhfOY8237dwUCGvEmrA1icFmbMeg9RQD81Xj7y31jLtu3TLVnhKCyH4NCSNG4OECcFgEeFDSJblpgXM3vTbIIQkSfoy/V34ILstWup2EwrdfYm8r127xjwczGYzIqHh3RazGaFB0hyZTCYcOXKke35o5OstCsheuQxX/7YWouJD1Qd70HDhCkq27AZkDT6fhsxljzMNWFV16JTJL4CHseEHiB08FAmPTkLjmg3QtHoUb90GX1kFGr64wIJY2YblIH3mVIO8g5WZt7fItEQyt2SuXILLf30TJp+Gqv0HcO3cWZS8swOyaIHqF5C6YjYE2TDtNGui0zNTUlKCtWvXMvx70++DbkY0Hvr90zk/2odAtxO4qqpsAi9duoQnnniifdLz0l2KAGng9OrqHxolMtN1CX3uHYmEh8ahbudeeOskfPrCj+E9fgqaxQx7QiLSFxi2awr5+iV90xojEbDxyYAnF6N0wxYoFrCYJxUffAxJFqA0+JExdzascfHMjdDEuMQgFIrBQ5EvSYtPHHM3+ky4DxU7PoTYIOLzZ/8Z9edzIUom2DL7IGP2TFbuhrtAJ2fq3LlzWLZsWSdbid7qtEBOigKF8OVH6Ah0O4HHx8fjjjvugMPhYFLTJHY1QYQO1+1bkh5zq6urUVBQ0OU2S5a9ifapS8DApXNx5P3doDzFtXs/gmCWoHt8SH9kKpz9splsLOhZi6kic5TxQdLD4xE7aiRqjx+DmleCuiu50C2A3CcOmUvnBGoRVbfUBoPv6H/f5YtQtmM/rIKImsOfQ7Ra4PF4kTVrGuxpKZRZgsUNbyFCJ97Q74G8UIYMGdLl2HdC7HZXra+vR1JSUrvr3c4Vup3A586di+nTp3PSjvJvIZm5yPPke9/7XpdLKlAWHoG2p0tIfnwG7BQf5WouLBYbVE2BapaRuWQh03wZ9RqhxVuVUzRbkbZ0Aao++RQWuwDNbIVa04D0OQ8iYdgw1gbtp2RRs4Ks3awlaj995gzEDB0Eb+4VyBY7NFWDbHcgc/kiVl9TVeZb3qxap05JqRkxYgTWrVvHfif0vjceZEoJauJciQtthrudwMnmTS9+RD8CwaekrpaUfszBVGnW+ARkzZ2JKz/7L6gOG1DrRdx9o5Ey+T4mFvvh34Lg0hc+htxXfgtvbSUkwQmIEjJXzmc6N9nLSeMP2EFuGColKjHHOZEzfxZO/efLsNgsLPhW2oRJSBk3lm1Aovyv12vwNzTUzg9oDYL7grcTtNugeNR4odwGWPf4IdJ6RXcdzZN3ZCyfDSk+HpLPD82vIWfRXIi0iSdAmzfT3kh3jc/ORsqMqdAbfNDdbsTeNRgZ0yYyzqZ+mOLdivZNYydLuEJ+5UsfhzMuiW3+MfmAtJXzAJny+ZDNvY3KnQCvt2rdnYCEVw3kSeBAcAR6DgI6kDBiOJKnPAxfXT1MfdORNn8G03xDGgRLoA1kPrEIsDmhueuRsXAOTLFxBnHfohG2mKkD8cOGIf6RB6HU18E2MAcZcx+9RU1+mSMQfgS4Bh5+THmLEUSANGjy085ZuQBe3Yv0xybDmZ0DlUK5tmX3aC4PeTrQppz7xyF+zDAIdiuylgQXL5sXbP2c+pYp8iAE9H1yMVTdh7THH4U9sU/rFfinHIEIItDtNvAIjo033QsRIOMEkXifRx5C7IixSJ09g2nOFJkwJBWaNolpOkSTjMzZj0CItSN2yCC0ne34OhDZJjPjs8wpExE3ZjzS5s0KFCLJwm8+uU4C/pYj0IQAJ/AmKPjJrRDQReOBTYmAjfdWfQevkxVeVHWIzliM/vmLiL3PiNlN+VdDoU6ycMsCmB07c+F8JD54P2uaciVT/VDaCMoi2OwY9euX4Lh7GBRdZ+0Gr/H/HIGuQIATeFeg3BP7CMTaJne64KKcrGuIB5CgULZ3I4880zl1SlAm3hDDJBLDpnsHJRvWdA0ZMyYzcwgFFWdeKiEpwLSx3sikY++fDUf/bKiaBk0QWdae9sqcMuEB+KlfVYMuN19qbW9LvDxHoP0IcBt4+zG7LWqougaVSEkQ4PV4cf53ryP1tTX4b2cGvna2DPsfWoDLr/weSmMjIz8iwVBM0J0Fj3l5iCLLXE9tUcxw8lFnm3dCUZ8pyYIgQg56m9D+INZexyWjXZuyTE8AoQjQ8X54TY7A9QhwDfx6RPj7AAIiy8zurqrE5099B0Xbt0KCH4mxSdD9HpQe2ImKA7tQsGMPxv31N7Cmp7HMNO0zQnCwOQIcgc4gwAm8M+j14rqUeUZTgbPP/RjF2zdCjumDfk8+gczp05ipoGj3HhT9aT0qd72HE9/+Psav/SP0gC92L4aFD40jEFUIcAKPqumIHmEEQUL53r0oXb8FojURd/7yRdzxzb9vEjBl5lQk3DUSn//jCyjeth3Fu/cga+ZjTdf5CUeAIxB5BLgNPPIY98geyJpbtnsffP4qJE2ciMHf/DpbrPOpOqAYvtT9/n4pEqdPBFQXKt77sEeOkwvNEejJCHAC78mzF2HZfcXFUOFDwt3DwAI8ka+J4IMuajBphrU7ccQItr3cU1IUYWl48xwBjsD1CHACvx4R/r4JAckeC3Kuc5WWMgcT9mURKbkCQH7TdLjLqqDBD9GW0FSPn3AEOAJdgwAn8K7BuUf2En//GJgRi9K9u1Bx4gQk5n5nZYG5JQG4dv4CKt7byUg+adzIHjlGLjRHoCcjwAm8J89eBGWnHY/Zcx6DefQIqEXFOP3ksyjasQOe+ka4G1wo3bMXnzz1NNx5ubDeNRLpy2ZHUBreNEeAI9AaAtwLpTVUeuhnRsoDw7bRWFgMS3wiRIcJEHTQ1pX2HIIGmBMTMOblF3Fw2TdRffozfLro67AOHcLyR7oufAGloQxSYhbG/vKncKSktKd5XpYjwBEIAwJcAw8DiNHSBO3oLv/sBD79hxew6/5pKN74LsgdUGBRqtsppQBomo74KRMx5e2/IWX6PMiqGXXHPkXtscPQdBlJ0+Zi/OY3kDbzYfhCjQbYTjF4cY4AR6BtBNqnlrXdDr8SBQjQ9vDibbuQ/+pvAMGE3HXrkP7UXJhI+27nLm9KVSbpAtO2Y8ePw4Qdq1D56TG4zl9m8QCtg/sj+d5RLBu7V9cgUXgR2s/ezn6iADYuAkegxyLACbzHTt11guuAKgD9V85F/p/+DLX2Guo/OoyaI0eRfJ+Rbuy6Gjd9KwsCVJEIXICuahQwBKnjxgL0anZQHG6KR6KJUltpJJuV5qccAY5AOBHgJpRwotmdbZHyq+mIGzIEFKdaalThdtei+M2tHZJKECXIghFhUJRESgjf6iEJEkSBylKSA35wBDgCXYkA/811JdoR7Ivs35TVm/5nPrEUfosFFosdZdt2wFtaHMGeedMcAY5AdyHACby7kI9Av4JkmKD7PPwAUseMhKoqqCrKRdHmHUZvOkV8JYrnB0eAI9AbEOAE3htmMZBJhswZdMhmC7KWz4fgVWE2mXH1ra1QfF6WhUanEIP84AhwBHoFApzAe8U03jiI5EWzYO07ELIko+GzY6j4cD9Tz/XgHvgbq/BPOAIcgR6GACfwHjZhoYrrSE1D8rzp8Ls98Gn1KHhjA9vKo4ttLUeG2jIvxxHgCEQLApzAo2UmIiBH9vLZsFpjIFtsKN29H9cuXoXAZzwCSPMmOQLdgwD/OXcP7hHvlZYqk8eOgXPSA5A9GjxllShcu6lNd8CIC8Q74AhwBMKOACfwsEMaHQ1S1naIEnKeWAAvJf+1mlC6cROUhsboEJBLwRHgCHQaAU7gnYYwWhvQQbvbs2dMgWVYf5YxvfbcBRTs+IAJTLsrNe5RGK2Tx+XiCISEACfwkGDqgYVoZ6aqwxSfgAGzZwIeD0y6iqK/rYWia9AlEQKj+B44Ni4yR4AjwBDgBN5LvwgiviTo7BVLIfdJhmKx49r+Q6g5fpJte1dBAWj5wRHgCPRUBDiB99SZu4XcAoUFlIzpdd45BOlTHobqccPbWIeCNVtYbSNU1S0a4pc5AhyBqEWAE3jUTk3nBWMkHtilmfHEXJhEEyxmC4rf3glXeTlE7lPYeZB5CxyBbkSAE3g3gt9VXdNiZtIjkxAzejRUVYNyIRelb2/nobu7agJ4PxyBCCHACTxCwEZTs7quw2yxI3vRHCiKD7DoyFuzGYqiGGJqOqgMPzgCHIGehQAn8J41Xx2SVgosVWYsngVnWiYEk4yaIydw7eAnrD1KBMGKcA7vEL68EkeguxDgBN5dyHdhvxRCVlN1OHKykTxrOvweBaLLi4I31zIpNIF8DnkutC6cEt4VRyAsCHACDwuM0d2Ixjy+KTM90P8riyBZ7IBNRMHOXajLLTSCXJEKzjk8uieSS8cRuA4BTuDXAdIb30qCCDngUphw31gk3zcOos8LX1EZijZuZbwtsGQPvXH0fEwcgd6LACfw3ju3rY5MkCRkPLkAflWCxWRB6erNUBpdLKO8wLf1tIoZ/5AjEK0IcAKP1pmJoFzJs6fBPmQAKLZs1dlTqNy5n2nhPN1aBEHnTXMEIoAAJ/AIgBrVTeo6nEnJyJz7CBSfD4IK5K5dx3RvgeeVj+qp48JxBK5HgBP49Yj0+vdGCKvs5UtgiouHxSTj2p5DuHb6bK8fOR8gR6C3IcAJvLfN6C3GowuAquuIGzkCiZPHwevzwHutAuWrjfgot6jOL3MEOAJRhAAn8CiajC4RRdchBTwGs1asBCQJsNhRsPkduK7VMFOKSskg+MER4AhEPQKcwKN+isIvYHDjZeqMhxE3bAQkTUPNxcuoeHtnwKWQO4SHH3XeIkcg/AhwAg8/plHeogA/OX1rOqx2BzIXzYPP74Es6ChctwG6qvJdmVE+g1w8jkAQAU7gQSRuk/+kW8sURjagZGctnglLWgokq4zSjz9F1ZFjbFc9D4tym3wh+DB7NAKcwHv09HVAeAHMWVAIxD6JGTQAGY9Mg+LyAXUNuLpqs2FG6UDTvApHgCPQtQhwAu9avKOyt6wnFkG32WCySijbuh0NxUVRKScXiiPAEWiJACfwlnjcZu90qACSJ45H0ph74NN1+ApKULJhB8OBzChGnHBuULnNvhh8uD0EAU7gPWSiIiWmoOsQzWZkLZ0LyatBs4ooXLsFitdjREbR+Qb7SGHP2+UIdBYBTuCdRbAH19chQNCMnZkZ82fCnNMXsiig6thRVO85yGzlVAa0+4cfHAGOQNQhwAk86qak4wLp0Jh7IAIbcTzuWlTXu9pskGiZuJmyqdnT0pA1exY0lw+iouLyqk1MA1cEIdhcm+3wCxwBjkD3IMAJvHtwj0Cvhm+3xkweRM0Kvr10Dp7/j7/etC9RBKSAgp3zxHzIsVaYLGaU79mLaxeusGs8Wc9NIeQXOQLdhgAn8G6DPtwdCxAgQZVoH46AfW+/gb9s24/S3C8MW3YI3cWPG4W4hyZB8fuhlFaiZPV6SGBRZ0OozYtwBDgCXY0AJ/CuRjyC/ZH2LUOEv+4qXvy3fwclUau+VoT6EEObEPFnr1gElqveLqFk4xZ4auoiKDFvmiPAEegMApzAO4NeFNUlRz8FCtuE88b/voYGJQZpThMK80tRVeMPSVJqI2PmNMQOvQOUyb7qwhWUv/dBSHV5IY4AR6DrEeAE3vWYR6RHMmObJRMKzx7CugO5+PkrL8FhVVFXXoiyitoQ+tShaRrMcTHIWTgLqkuDRVVR8NZGaLQ4yg+OAEcg6hDgBB51U9IZgXT84mf/hSnLv4YpD90N0dEHja5KXC4qCaFRysdjrGZmLJ8LIbUPZKuMqgMHUXvsc6M+JT4mlxV+cAQ4AlGBACfwqJiGjguhawo0jVmtcezdv+JshR3fXvYIdJiQ7HBA93pw5UIu60DTfTd3CQx8G2KHDEHmIw/B51Gh1DUgb9VmVl9XdSg67d3kB0eAIxANCHACj4ZZ6IQMuiBCECSo/jr8x+vr8dyP/gVOARAcqRje18ks4+VFl1kPTMOmULJtHOTHQjo4vfquWAhRskCwy6jYvAveynIKYwiJ+xS2gR7/mCPQ9QhwAu96zMPYI23dEZjb4IY//QbnSvxINXtw+ONDOHLkCBrhhCSIOH01P2DFFsE2+7QhQXPzSJ+pDyNh9DBImgrXlcso3rDNMLAI5FjID44ARyAaEJCjQQguQ8cQ0HQBogC4qi7j9b9uwKD0gXjl5V9AVxWYzGYUl9TBIplQnnsJNaqORIkIvG0TSDDELEkjm83IXjIHlRQfnOKjrN6CrK9/BbKJf2U6Nlu8Fkcg/AjwX2P4Me2yFoOPT7/92YvIHr8Sf3zley363vHWK5j95PNorKxEVbUXiclWttmnRaE23pDfSfLCx2H71evQqkpRefQUKj/6GOlTHmqjBv+YI8AR6GoEghzQ1f3y/sKBgACUnNqP1TvP4h++/+wNLWb27QuHXUJ5ZSWKikqN6yEGphJ1wJnTF8lzpsDnckNwe1H0xqob+uAfcAQ4At2HACfw7sO+gz1rIFeS4FLkf/3sP3H/nG9iZKoNTR8GWk5O6YfUWDvctSXIL6lgnwo3MaE0F4gy05MW3n/5fEiOGAg2GcUfHETVydNQG91NRUkOTQWMTPZBqZou8xOOAEcggghwAo8guBFpWhdBW+bJU+TYvnXY8lk5vvvsExRX8IbuUtJS0D8rGVBcuJqXH7hu+HrfUPiGD1TKe4y4CQ8g9dGp0Pwe6LXX8MnCJ7Bv4iwcmP0Urv55NVTFDxYwRTGiGt7QDP+AI8ARiBgCnMAjBm2EGqaclqKEhpqr+NYz38WIGcswKM0ecP5r2acYmwlHfCIj9/Ofn2QXBUpoHMIhQjSiFDbWQ/V6oFFYWbcLvst5qDp2BPnvrMexr/0DDix7Gt7qaggmajfUm0MIAvAiHAGOwC0R4IuYt4Qougr43TXYuPbPeOVXf8CnZ4owLPkQXnv9z5g8eTIG9+/HhNW8tdj5/h4cOvwxPjh4nH22+c0/44UMG2ZNmYnJD4y85aAoEBaZak7+87+jbPu7QEwcMmbPQsrMqTBDQOH7+1C8cRMqNq7FaasV9/z1fyBI/Ot0S2B5AY5AGBHgv7gwgtkVTfm9HpSVVWHuE9/Ed9L7oLK8GHlX81HX4IHO7NYiFF8jCvOvQLLE4Ze/fg1mq4CGijrkVxSj/FqtYWwJbIlv7jrYXH5RFFB+8DDy/rwemtmM4T/8Jwz9wT+xLD1ULn3lQnwxZhgufP/fUbJ2A8qeWoqMRx9u3gQ/5whwBCKMACfwCAMc7ubt8Wn4zvdfarVZTfNBgwliTAa+8cwLrZahD8labuy5bLMIu1Dyzm4o7jIkTJmBIT/4DvtM0TXIqgBNFjD0uW+i4r09KNixDYXb93ACvzmc/CpHIOwIhGYQDXu3vMEOI0Cas2pk31GhQaFTTTe0b1GCLGiQNR9Lk9a0s5KCULFN9WCRBUO1VHuKCiDBh9R77gaFulJVWqnUWBo2UVeZxTv2vlEwUav5hR0eUmsV2ZIsjY1JfuMCbWt1mn8WTMVM9YPnza/f6pzqGHVvVZJf5wh0HwJcA+8+7DvWM8UiCexml4hCiY1ZfBIBbDLZ++B29wBVB4oZkx24Z4fA4rLVwZJCeCsCSR0o7gpL2eaHpomQJUCvrIMGP0SLtWPjaaMWS+spAKqqs+EJtOW0HQfF3NLIjM+2LuntXl/VVaJvAaokwGQ8srSjd16UI9A1CHANvGtw7pG9xI0eCRUxKN/7AeouXIJJFCFKAhTJDFmSUZdfiOKdewA4kHjP3WEdIznLCBTphW5OIXrONBeA6km6BonZ+ttH/tSORtZ+QYTopeccfnAEohMBTuDROS/dLhVFTMlcNAMJQ++CJ/8yTj75DEo//hSqqkFUNFR/+jk+/erTcF/6Ao6+A5GyfFZYZA6aO1xlZfji969DFztInyJQ8Jc1qDp6rEn7bo8hRpAEuIsLceFXrzXVD8sAeSMcgTAiwAk8jGD2pqYEXcvATIEAABA5SURBVIU1ORUjX/4RTLFJqDxyAJ/MXoGDU+bj0NR5+GjWIlTt/QCyIwGjf/ETOLJyDO+WToBAtnzKCkRHxf5PcObFl+EtLA2ZQMnmH7T764qKL155DXnrtxre6YFkFLQJKpSDjFCVH+zHhZd/DXdBsbGGQPb/0KqH0gUvwxHoNAKcwDsNYe9sgHiK7MjJj0/H+HV/g+P+hyE2+uD77CgaDx9myY5TRk/EmLWvIXPJHIhqyDzbNmC0SYmFq9VRunEz3GW5KN/6gUHAbddq9cq1A5+g/uw5VG//AL76OrbwKmiAqIVmTqHxF63fgcaqKyjZuI31Ieki9JvEU29VEP4hRyCCCHACjyC4PblpgVZKBR2CriFl+iRM278Jlc8sx3/7GvHhgExM2PgGHti/AemzpkNRSPNVmrTfDo2bac9k8wZqTp9B6YeH4JDsyF+3DprfyDh0q3YNe7lB0JdXbYAm+OA6fx7F7xg3AYUWNSlKVwhH7YlTqDp4AGZzAvLXbwH537M7Cc9IFAJ6vEhXIcAJvKuQ7mH90BdDp3U8wciDKZssqBvSH9uVOuzJiEXW7EdgdsaCIozLkgBBDhTu6DgFsO36VL1g0zag7Bps9gRUffoZKvYfYq2qutq2CUMHFNVwbawvyEPJzj0QnQ4QaReuXs/ix1BGIkqA0dah6jpUCgADIH/Nevhr62C3x6LmxElU7t1vOPsQKPzgCEQJAvzbGCUTEXViMG9F2u5DKdsM0pN8fiamo5lCzDYEMTfFYErkjo6EMguJ8NbVonTTTmgOE3xmGfAoKHhzI7NBU3yWti0Y5G5oyFm+8T0oBSWQTBbIDgeq93+MmuOfMw1aCBB0W1LSDlRXdRWKt+yCZLOzG4Dm86L0zbeNKh3wiGmrL/45R6CzCHAC7yyCvH5YECC9l/zUy3Z8gIZz52E2W1gCZYvDicode1Cfe4kRtNYGg1OYc0EU4ff4UbjmXUhmiZl06DO1thb5qzYw93nhJl4tgm7sTy17dydcl65CNJlBFhez3YGy3R+h7uIllgEpLAPmjXAEwoAAJ/AwgMibCB8Cxavfhl/ws5grgqJDtQCNFaUoWvcu68QIpNtaf/SsAFR9dBDXTh6DFmMG1SeTCWnSBe9uh6u86qY+5aTAa5qCklVboEk6ZCjQRB2iJKOxsgiF67cGZDDMSvottPnWpOSfcQTCiQAn8HCiydvqMAJk/Kg5cx6l+w/BarLAHJ+E/n+3DJJHBcwySjfsgN/daIS4baUXqk8OiFfXbIKgeCE3+JC18HH0GTkSoibCffEqit7ZcdMYMETg1cdOouLwUZgtFlhS+mDAt5+C4BeMvKDr34W/wcV6pyeGgMWmFWn4RxyBrkGAE3jX4Mx7CQGBolWbodRUQ3NpiH3gXtz50g9gyerLtOa6E6dRuvvATVtpvJqH6p17IFgc0CUrBvzgWaQvnQuv3w2TbELpqg3Q1baTOlPjxas2Q6utg+pywz7pQQz5wfMw5WRC0mW4Tp9H5a69bBmUbhg6Z/Cbzge/GHkEOIFHHuNe10Nws0znB0buh0Yr/poaFG/eDrNVht8kIm3RTOblkjJnGjS3F4rgRtEbm1hhowrbmcOyBgXlKVz3DnxFJfD7fYh7cAzihgxF8uNTYctIgmqWUH34M1R//ClrQ2PBUnSoFLQqYAqpL6tE4bb3Wfo40vqzF85i9u+seY9BcylQBQ9yV9GCKhlmhBvcJjUK4KIFYo11EpzgmDrZDK/eyxHgBN7LJzgSw5OkYLCszrZOnidGGyXbd6H24mVGigl3DUXmtMnsQvbyObAmJMFsklH64X7UnL1gVAj4jRPR0d4ct8eNos3bIFrMgO5D5rL5TFOOycxC6owpEF0+aC4f8gIeLcFog4y7A3eRsm274Mm9Cl3TEH/3cKRNmsD6Sl8+D3JiIkxmEyr3HkDd6VNsY1DT3Ye0cYqcKIhQRTAzT2d/WEGPGovFYoyX/+UItIIAj0bYCij8o9YRILIURRG1tbXYuXPnDRpo67Xa/pRpv6Aoijosv38DVlmHy6/gjoVzITntzHc7btRIJEycgKqt70FxV6FkzSbE/+QHRmpmQYDIyFdE1e79aDhxApoZsGUORM7MR1kMXbpBZC1fjqurt8Om+lG+/QM0FubBmdUXfgq9S4EKJRGKqqFo7XqYBBkev4KsRfMhW+2sjfjhdyF5yoMo2/QO9MYa5L+1FcN/SlmNAncfZk4B3Jev4urv/gq9fwaKB2axaIZflmgbh9auBLE+ffp0k3tka+X4Z7c3ApzAb+/5b9foKU4JvS5evIhZs8IRvEqHKmgYrJnwn/ZUOK0i7HIyMhY/bkQBpxuGIGLAivkofe99mCUJuW9vQ7/vfhOm+ASIGu3fN1z/Sldthl9VIPglZM14HJaUZFAcQfJNSXjwfiSOHYXawwehFBegdMN2DPrHb7Ft9QL1JAioPnQU1Z98ClgkOOL7IG3JHIYNmVpoe3/mEwtQ+vYOCFYdBVt34I7vPQc5Mc5IME03EgCf/+AlFG14E4IUg+eFehRAgRwg+Y6aREwmE5PD7zd88Ns1Ybxwr0eAE3ivn+LwDdButyMlJQUxMTGd1r4NqXSQ3ThdsMBU5kZDTRXSv7oQMUMGMQKXRMMQkfLYNDjv6gvv+ctwn7uEsp0fot/S+dDJ+VsUUXPpAor37oPZZoUumJGzbC5rXmK0CmZ+yVj6OGr2HYBsEZC/fjv6fetrEC0WNg7SkgvWr4fq8jK6TZk+FTE5mawNSiBNNvfUqZPhGDEYnnNfwHvhPArf24V+KxdBVVXIsozqU+dRsXcfbHHJUEUZOQnxICdycyCIVkdngUwpjY2NiI+PN2QN2pw62iCv16sQ4ATeq6YzMoMh7ZFey5cvx7x585gZJRw9kQlFoABRUOA69Anqz11Gv6cWMndAtt8mYEiWY+zIWDAfl378c5gFGQVvrUffJXOgiQZFl659B/7SKsiyiPjHHkLcuOE3iJc1byZyf/Ea3OV5qDt6EqX7DiDr0anQBRGe0lJUbPsAZrKfawLSV85vUZ/ktDjtyFowH6f/7f/CKssoems9+q2Yz8ibbgBFazZBr6qBzwqkPzITb7/+8k19zlt0cIs39NRDNwn6TyasoH38FtX45dsAAU7gt8Ekh2OIRBpOp5O9wtHeDW3MmQ3MAdgufXLovs543G/xQuT99k/QGxpRfeAAqo6eQNLYMfA1NCB/0zswWWUofg19l86DIEjGTSDQCZnJHWnpSJ77KC69+lu2QafwrU2MwKlI8cadaMjLg2iWEH/fPUh5cHwL8YI3k8xl83Dxd79nboYVhw+h7pPPEXf/aHiqa1Gy+R2Idhmq5kPmV5ciqU9yizbC8YYInB8cgeYIdHaxvHlb/LyXIkDkHSmtj8wTzC0wcEL+Lcxy0ozAyWMkdugAJE+ZBI+vEXpNI/LWbWEcX7HnIOrPfs52TsYOGYD0mY8ZdmmjVTYjwaZyls2BxZkAk82C6h0foi63kC2GXt2wAbLFBEVRkLN4LvM2aT6VFOWFvMedA/sideokaG4P1FoVl9auY8UqduxCw+XL7GkidthIpD86qXn1sJ1z7TtsUPaahjiB95qp7JkDIXJlBBs4CZJt89FQHG8i0H4rFsACG2Azo+LtXfDVVKFiw7tGUmeXgpQ5M2BNjAOVb94Omcp9APqMG42EB+6H5FLhrqhE+bs7UHvqJOo/OQFREhGXlYWMhbMND5eAayHJQbk1hYD2O3D5QsDqgNUqo+ydD+ApL0Pelh2sjOZWkD1vFsxOR+Cu1HwU/JwjEH4EOIGHH1PeYpgRYDkYNKDPtImIHz2KIpTAW1qE0//6c1R8cggmsw1CQjzSly0wehaCidmCb3WIqgpNlNF3xXy4RAGS3YzCtWtx6af/w+KGqy4fkh+fAnt6BkAbclosFhpxyimwVeKUiYgdPRI+eKCUl+HsP/8HGo6chFUyQUxLQtrS2WEePW+OI9A2ApzA28aGX4kSBEibpi+qbLEhlQjSo0AwmZD35iZ4Kqugen1IfXAC+owaZkjcSgZ78mihdrJmTUPckP5QRQ11p75A6bY9MNHW+xgL0pcsYfWvD1jIagpGfclsRs7ix+H3qdDN5L2yFd6GaigeD9ImT0DC4CFssZFn7omSL08vF4MTeC+f4F4xPMbgzFLOtrc7MnOgKn5IkggZEmRVQubyuU1mE/IMN7zDA6MP2PDZTSA+HqnzZ8BU74MmmyDS4mejFyljxiL5gXsNy7l4/Tb5QGsBuwxt83dk9IXsViDaJKaxC6IF6cvns/rXm3B6xRzwQUQlApzAo3JauFDNEaDt7pQthyjckZONpJnToDbUMcJWXF7Y7xqIlFlTm1e56XnWisUQk2Jh8hNRK1A0BWmLFzA3RAoRq1Js8RYmlJbNxWRkIW3Go/BTjBZS1xs1mEfdhZRpDzPvF5YXiAzv/OAIRBgBTuARBpg333kEiEuba9RZK+dAtDohaD74FDfS586ENSY2pI4oEFXSnXcgfsoE+BsboPn9sOVkIXX+9Kb6N6NeWtuk631XzoVss0FQAcVXj5yFs2Gx2dnWflG+WQtN3fATjkCnEeAE3mkIeQORRoCsz1Jgyzz1lTz+XqSMvQ9KfR1MSQnIXmaYLkJx/aCEPqTJkxZOKXr0Oi8yZ09HTFoKGwalVJOajDE3jowWVMkbO+mBMYi7fwz8dfUwZSYjO7D1njR39qPiHH4jePyTsCPACTzskPIGI4qADphkCzKWz4NHrUOfhx9E3PA7WYjXUPrVITICzpg+Fc5hQ6HJEjJXBLxXQmpAZ9EKRcmMjJVLICkNyJg8HbH9+4VSm5fhCIQVAU7gYYWTNxZ5BIzFzPT50+FMG4yM+TOZRi2q9Pmt1V6WO1PTYbbZ0WfmNMSNGYaksaPQ0vGw7VGQdk69MC3+8WkwZw1G6uIZ7L0hWdt1+RWOQLgRkF588cUXw90ob48jEDkEKAAWYHI6IThikPzoREixMZB00fA1vEXHAi2GBhYprfF94LhzMOKG3QWREjywhctb3AQCdakUZby3JKeiz8TxEB0OVv0WtW8hHb/MEWgfAoLe0TiX7euHl+YIhAUB8hJRyI5NyYbJXw8SWzgk7ZdCz96KQJmWHMjAQ/ZqsmmTh4uJdOhQCLzZKGh3KLVHGX1ok48kNV9qbVaQn3IEIoQAD2YVIWB5s5FCgEhXh5mYV5IRXJQUhLbz1TeXhEwlRPL0ooQOFPbKyC/U/p8CxVFkmenpZqJTu+1vo7ls/Jwj0F4EuAbeXsR4eY4AR4AjECUI8EXMKJkILgZHgCPAEWgvApzA24sYL88R4AhwBKIEAU7gUTIRXAyOAEeAI9BeBDiBtxcxXp4jwBHgCEQJApzAo2QiuBgcAY4AR6C9CHACby9ivDxHgCPAEYgSBDiBR8lEcDE4AhwBjkB7EeAE3l7EeHmOAEeAIxAlCHACj5KJ4GJwBDgCHIH2IsAJvL2I8fIcAY4ARyBKEOAEHiUTwcXgCHAEOALtRYATeHsR4+U5AhwBjkCUIPD/AL86cUs+eLWYAAAAAElFTkSuQmCC />
1.It increases.
2.It decreases.
3.It doesnt change."