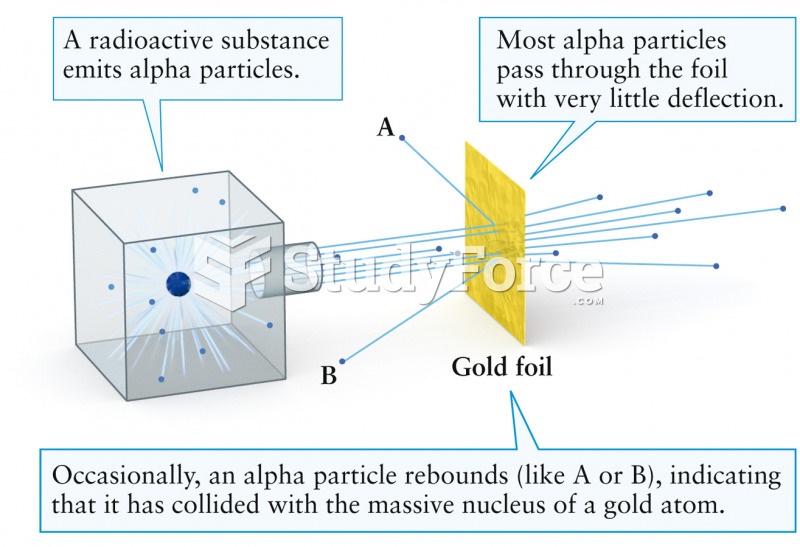
The solvent used in this experiment is toluene. Draw one of the Diels-Alder products from the reaction of toluene with maleic anhydride. Why is this product not formed?
Question 2SXlaZ+rguBfZh7CVxIgARIIIoGff/5Z55IvKCiQ48eP6yD3QRSHp7YwASqiFr44FC1MCeRny5T+rWRScYB6dxQcQxbIur8PEA99m9w1x/0kQAIkUGUC48ePl2nTpskzzzwjI0eOrHJ7bCB0CVARDd1ry57ZnMChzWtk/rNzZPris8vvpbsUn5wqI5Puk5iWEaU38z0JkAAJBJ1AQkKCbNu2TQ4ePCjnnXde0OWhANYlQEXUuteGkpGAJlBYcFIOH86Vn1RmEpRq1etIZP0IqelZdCd9DP+RAAmQQCAJwFEpNzdXOzIF8rw8l/0IUBG13zWjxCRAAiRAAiQQEAI52Zvk9RWLZfnKLHl3Z7FlusMhsY4O0iWum3Tv1llaRjCTW0AuRoiehIpoiF5YdosESIAESIAEKk2gYL/MH/6gDH3etWlQ6Xbjxy2R1El9pTH10dJY+N5DAlREPQTFaiRAAiRAAiQQDgQKDmVInyZdizO9ne1xbHyiNL+ihhzbmyXp75aJ26EqJcvOvBRpU/Nsfb4jAU8IUBH1hBLrkAAJkAAJkEA4EDip0g3XNtMNF3V4SNo6eaLvbVKvlGF6fk62rEoZKwOnlwrvwTBy4XCH+LyPVER9jpQNkgAJkAAJkIAdCRRKxuNR0nW6OdsZKyv2rJKeLSuOUHwoY4o06TqppLPJK/ZJSk9mUCoBwjduCVARdYuIFUiABEiABEgg9AkUHsmQqPpdS5JlpGblyrDoipVQk0jmlE4SN8m0JU2WfadTpCmjeph4+OqGABVRN4C4mwRIgARIgATCgcCu+QniGFq81B6bKrmZwzzL1pavlvNrnV3OT9uZJ0k0Fg2HW8YnfaQi6hOMbIQESIAESIAE7EygQJb2ry79Fhf1YfKGwzKxUz0PO1Qoa0ZESfycoiX9+LSdsjqpjYfHslq4E6AiGu53APtPAiRAAiRAApIv8xNqiTkhmro1T4a199wFfv/KEdKs1xzNMXZGlmSOjiZTEvCIABVRjzCxEgmQAAmQAAmEMoGTShGtXaKILtiTJwNaeq6IFuxaKNUdA4sAxaapZf0kz5b1Qxkp++YRASqiHmFiJRIgARIgARIIZQI5MrdTpAzXPkcO2Zi7Q2Lc+ymVAKEiWoKCb7wkQEXUS2CsTgIkQAIkQAKhR6DsjGiaWppPquTSvCM5XTandBcmWgq9u8QfPaIi6g+qbJMESIAESIAEbEWgajaiu+b3Vx73RZ5O8albZfWw9rbqPYUNHgEqosFjzzOTAAmQAAmQgGUIbJubIFHDi8I3Ocatk63Tuohn4UCPyMy29WVMcRx87zzuLdN9ChIkAlREgwSepyUBEiABEiABKxEoyFYOR62KHY7EIemHd0h3DyI45WyaKZG3jCnuSryyL13tlX2plRhQlsAToCIaeOY8IwmQAAmQAAlYkICyE+2kPOfNJEmxM+Tg26Ol8bmmRXM2Sf/IW6Q4/Kg4ktVMaoqnM6kWRECRAk6AimjAkfOEJEACJEACJGBNAoX7V0q1Zr3OCudIlg1rJkunxs6hnI5sXiqJHfqJqbeKxEtW3mqJdq56tj2+I4FyBKiIlgPCjyRAAiRAAiQQzgRKB6c3OcQnz5DEO26UqyIvkFNf75H1L6fI9PRio9DiSmkqN32SB7npzTb5SgIgQEWU9wEJkAAJkAAJkEAZAtlrpkir+ElltlX8wSELstbJgGgPDEorboR7wpQAFdEwvfDsNgmQAAmQAAmck0D+IVmzYL7MGT691PJ7qSMciTJjzBAZeHeMRDBoaCkwfOsNASqi3tBiXRIgARIgARIIOwKFcjLnsOR++5OcRt+rVZc6tWtLxGU0Bg27W8EPHaYi6geobJIESIAESIAESIAESMA9ASqi7hmxBgmQAAmQAAmQAAmQgB8IUBH1A1Q2SQIkQAIkQAIkQAIk4J4AFVH3jFiDBEiABEiABEiABEjADwSoiPoBKpskARIgARIgARIgARJwT4CKqHtGrEECJEACJEACJEACJOAHAlRE/QCVTZIACZAACZAACZAACbgnQEXUPSPWIAESIAESIAESIAES8AMBKqJ+gMomSYAESIAESIAESIAE3BOgIuqeEWuQAAmQAAmQAAmQAAn4gQAVUT9AZZMkQAIkQAIkQAIkQALuCVARdc+INUiABEiABEiABEiABPxAgIqoH6CySRIgARIgARIgARIgAfcEqIi6Z8QaJEACJEACJEACJEACfiBARdQPUNkkCZAACZAACZAACZCAewJURN0zYg0SIAESIAESIAESIAE/EKAi6geobJIESIAESIAESIAESMA9ASqi7hmxBgmQAAmQAAmQAAmQgB8IUBH1A1Q2SQIkQAIkQAIkQAIk4J4AFVH3jFiDBEiABEiABEiABEjADwSoiPoBKpskARIgARIgARIgARJwT+D/AcUI5paa/rN+AAAAAElFTkSuQmCC />
The aromaticity of toluene is lost when it undergoes a Diels-Alder reaction. Therefore
Question 3The anhydrides formed in this experiment are reacted with aqueous NaOH followed by acidification. Reaction with NaOCH3 followed by an acidic workup also produces a new product. Write the structure of this product(s) and explain why it would not be a good derivative to use to characterize the Diels-Alder product.
Question 4opOnYEq4IifYHZFwJZfeMTRfFHMf1YTScfGH3de5MhqJ5dccollpJMrHC8u3Lp1q+DZM65Yw91YUGMhjmfMeB0BtswQUBsMvY9+4nyqDZb0aC6C1dUO1q+kVSx5LVARW2A6fOMV1hHmeH3qxDmOvzf2EchMWRLnFlfzk0BDQ4PgASazfTf/WYU7HRt3dvbu3SvYWBCvuzXT439TVeerX/2q4HyN1rpXFv5qamqMdSFs3VbNExvuYOMcu3btEseOHbMg6VFcNrDRHd01UU3K4vZ4c8zhULWS/tD1l5YMRA666lUDQCWxNZtuCVYyHlMQtLZxA1Hz8MNvQ+1KhHOpEGAtH14/pL636v6SJUtyxoIn98/YsiD3AdUysOPiZcuWib/7u7+LGk1Tr995550JzcanwjM+7EB3kyhT13erQpbNvr+60XEGV/22Q7CKJ53Hx/zh47VP6ktr7j/wwAOjVnJWE2F1kb/5m78RbMHGzAP/jxs3zhiVYLOxPPWtK2ixmor5MefZMGyZI6AKVp6KeseGSDeHaoOlvis6+8PvFKTDMph1xkon/2qY4ZdFlzTC5QMB9tfHa2TVd8fc//a3vz1qRWTVpB//+Mfir/7qr8T5559vyQ8LWqy5sHHjRvH4448Lt3xosbYEC25r164VF110kSVNHv1m40us1cBrb1lt3HnrEpVKh8vjr3E2vhOJpCcUtKQ3dE1mp6hQOmveykbn5I0r6lovEh7VCplbgpVcW1UfDIiysirREadvaM6weatCSfKJy24T4AEBHohW1W3NOmz+X3vttTm7ttEsA6/n47WarDl13nnnGcbGuL1g9zhmGLfZDo2vT7Q31Ai/o69NjygL8PKExBZn1H6KnapgfLpqP8lXnf11DKqAcU+QhZOf/OQngnVSzZfV/OcPXDAYjLtjdA+5EfnZz35mmMk0hSMzfzyqyD60eFTx1VdfdcwYj3aY97D6CbbMEbA2GCmo0ThkWW2wzGes+z98YcTaqXHHMhgEK4dHjNMuEDDbebaEalc/tm/f7kIqw4+iq6tL7N6923b2iLUMFi1aZKzT/b//+z+hu2aCVclZnYgH09gymbq+lxnw6PhXvvIV8dhjj6U8S2adYZIqQ76AaO+Jkz4MHAOitS7m7NNgL9c9xeapY8y6GmLOSTkcj4DbOSwZ6GkXVSWqU3WP1eCFW4JVLGuWva6moPBEhMChAqIlKA5cJrBv374hgwLx9bm4uDhn1jHa4THLY17jtiveyEV8GDNsOv/ZBUxnR7vo7A6L7s4O0dnVM+KB4XTmdzTjhmCl0GYnaezo13xJ1X8eweMRxWzb2Dkxm0u/6aabjBEMNc/sTZx9rrATS/5Q88bqJxyGdXdZ9WXixIlJRiOzrcT5lR9VsIr39TCckqqClRsezbvbG6S6YJlh/aqkRBrLCNZLq1rxOVMFK7csg1kFKzfKEp9rHBcmATYp/Jd/+Ze27Ty3jaOpkaD7BHigjPPFvhJVC1+cX/428YJ3XvOrWhbjDthvfvMbQxWY11vErzthh/a8oJ2/a24s5g9VKwZsIoKGPxAUDU0h0doaEg211cJvcbHAazZKhLNtCqma6I9b10FeUVFVY8QZamoQwcDQdR3+mriF9WkRrMKitqJEeJWZOvIln6nTfd4Il5jAkSNHDGfdan/Hbv8zn/lMyoMEiVMe/atmuRKlrBMm0f245i4BCFaSJ4/ksTodT6+aL6j6z2ub2B9JLmys2mKa2Iw3tsGzcJdddplRRtalr5ZrbLicPEKJLTMEVMEq3jt5shwN9A0dEVYFK+s6APvYnD2aD4jGqqEdpcF64RMNFhPI8eukhkhe9okbZ9WF4qplMKtgNbKyJEgelwqGgJ2rDLWdZ1Uinu3P9o0FppdfftnwlRhvpZbLw+0+D7TxoJlaPt5nAYvdhfD9HI+724BoCqpWPuOForhjj180WtoRm9xIp+NVikn2+PLEH/uDNovl0yRYVatClSFIcnkSq0DZlBCnUiDAdZjrqN27Hf8u8CC5W2qzKWTR9aBmuRJFrBMm0f245i6Bghes2I7/VVddNeQDZL6obAqT1zjl4sbqLFyOL3/5y4Knw9l/Aq/T4kXIvLEpT/4IX3fddblYvPzIs8X/k1fbD0xrxLy5V5pcr27ojLKwClZ2CjbRoMaOKtipqoADnXXROuGVFrbau+S0f6hO+M3OhNeqvpMOy2BulcVaYhwVIoEXX3xxiKsMs43nfxaqghlW8x7uczHL8Y1vfMPwicNtOq+Z4jLxQBo7IzXDDDeNVO7r624XNXImyVSPM9I22w3J2uMrEzUN7UJfBBkQnU11oqJE8fdnCDIxQc3nD4imoVPpg9lWBauUza1LYxwO40R9cl1cj1TN7wzVCp+ZnxRcTaTCFGGFaG9vN/oq5ruc6J/7OPHqcrnK0CxnovzrhEl0P665S6BgBSu2tMS+SVQTlebLaf7zDBbrsOfqxqM7XD4WqsyNp9BVvynLly83rFCdOHHCDIL/USXQI6oVvw8lwTg1Ftu8dFkWdqv3uCWMtFZFrAVKAUrtVwx01EQ6aT7RpFxIh2Uwt8piixAnC4IArz9in4Hxs/dmG8//vHaW1aVzdTPLYuafNTBYBVBt5+PDmGHT+98nurs6ZYe4UxoO6BYdHZ1SEBk6y55KHgbCPca6jvaOLhl3h2jnOG1m7lOJ042wAx21kXbRY3HY7kbchR4HC0is5qqaITffZ7t/Vm9VzZLnOj+zjInKoRMm0f245i6BghSs2BJSvBlL88U0/9ncbFOTjVqBu/zTHhvr5HPHwcl3Q3Nzs/FBSJdZ4bQXMA8S6KxTzQRb/bnYFc9qVtga3i1hpLu13lhbFajrsGYhOsNmFayEcN8ymFtlsRYAR4VC4KmnnjJ8A5ptut0/G3DIxrWzqTwjs1yJ7tEJk+h+XJME+rpFU0OdqKkLDZ1tk7Ni5qxVlfOisTzCGBYd7a3GLBLPJDn92D9Tp9R2CDsKv5F4pC+kji5lpC5CigeH7dRdzfc5/v8LX/hC3vnkNMuY6OXRCZPoflxzl0BBCVYsXLBpWfMldPpnc7cHDhxwl3SGYuPOBZczkd8tLi9bGMSWKQJWoYTILxo67NT4BkR7fZVFxSbeRHtahZG+ThH0m9a3KqQoZd3ctgyW1rJYs46jPCJw8uRJ8aUvfSlpO8+z+Q8//HDOl9z8jiUqiE6YRPfjmhDh1qrIO+W1zNYbbLrro+1ysF1fyTFnucoBNtOnl/luJfv3llSKxs44NpZ4FN9jChhe354sbr7O7nFYEMu3zSx7onLphEl0P665S6AgBCtepPvQQw+JqVOnJq2gF154oaFG4S7mzMbG1gF5bZXTVl5ebnB5/vnnnYLgfJoJ9LWbKnaxdQPekgo5Oio9m0tngQ11QRuLWmUi/hueDmGkr71WlMiZT7Px5v9g+9DRRUbkpmWwdJQlzY8R0WeYAFs9nTFjhuVdVd9bc59VAzlsPmxmmRKVRSdMovtxTRIIx2alvBV1MRPx4XYRiKpzlw3xcZWX7NR1a/J7YL5fyf+9zqbwKV4LIkaO1w8mipvXkeejUMUEzHLHaAzd0wkz9C6cSReBvBesXpVmam+44Yboy2m+gHb/F198sXjllVfSxTpj8Zqjt06C0xtvvGHw8fl8GcsjEpbKdA3miKjGh8pTJpq6h65XSIcwEhupjeWLfcrEjT1GHqF7lsHSURa8Z/lJ4A9/+INYtWqVVjvPZsd//vOf5w0I81uWqEA6YRLdj2uDBNprVPPuXuH3Wy2nVjV2FwYqVbDyVoomqfJnpw4YapIq5X7roByV1Ma+HWo8CQQrFpquv/562/p95513psHCZfY8Rp26qxMme0qU/znJgGDllm6uHECSi1dbW9tFa3uHZYG9+dh++tOfinHjxtlWRvNFNP/Zp1NnZ6d5a179swokl/O2225zLNfChQuNxaFsKRBbBgmEO0VdVYWzmoXHJwK1TbbvO+daFUZc82g+IB0AdveIcE+nqK2MGLWQ71Nlgk6EG5bB0lKWDD7aQkvabJ/tOlyxcx2iQ7a73T1hR+eSZjxO7Ty7i+A1sWZbnuh/zJgxOWvl1en9M
Question 5cvrdJ3P64RJdD+uxQiwOvYQNThpOr6u1U59O3ZfXu2pApGGpcUOyzpiX8zSojILyCrwrfajdQY6VvE13cWY7zMbIHPfbUB2PSmzrIlypRMm0f245i6B0ResLDq1sRFw88Ww+7fVzZUcQlWxkRBfsHUImUOHDhkmxu3iVM/Nmzcv6kB3SCR5cmLu3LmCTcc7mSBlv1bM5Pvf/36elDjXizEgerqlRS05cNAlzfp2ygXC2eHZvE/UmuusyuocO8Mx+u5bBovFjb1sJqC2z2p767wvnb8Gh86EqvHYtfPHjh0zVJ2d4x38zvAgGxsuyrfNLHeicumESXQ/rsUTGGzXeDC2Sw46FdymClZxlmPtWfSIKsU5dHWrqUreLQLmeY14eEBm/PjxRl/ln/7pn/JeqGKWOnVXJ4z9c8HZdBAYfcFKrZAj0c2VNNQRbdUHjwqKFyebL53dP8/UuOF1Xk0zG/fZqR6Xv7a21jZ7bJaYVWTmzJljex0nC4tAd3uTqJPCdpONw8vWatMUe1VsnUFh4UFpNQio7bNd2+t0zlvZYBHY1Xic2nk2NsQDR05xnnvuuTntOiMRbrPMIw2T6H5cAwELAbUfpyEQSf0iUW0KULIfErOc2CdqIg6gvZWNliScDtiYxdatW50u59151O/ce6SZFaxGopsrWet8cPmROFkCXLx4sejpKYzRJvZtwgu22Rmy03bLLbcYHZPf//73TkFwviAIxD6C3sBQlwNRZ8AlNTFd+YLggkKmQkBtnyuk+mpHh51Z5pCorwkMUa2q6YjpBKnxOAlWnC82UGR2QtR/HuFm66j5upllTVQ+nTCJ7sc1ELAQUAUrDVXAcGtQqZtWFyHtNWXGtYraONcelgQL90Cn7uqEKVyCo1/yzApWGhXSUTdXsgqZTkzlCEiJjSqgiZNnY4qKipSKTYYH77D0ml5IGzsD5grIC73ttmeffda4zoIotsImEJ2VIq+obY8NPnTUB6L1yI8PYWG/JElKrwpEMdUfh5v6OkSlJ6YargpQuu08x/yVr3wl+n5yWzdx4sS88EfoQM04rdOp0gmTKA1cAwELAVWw8lYJNtnBTnktv74+Q529qc7qIoRk+NgXxRIrDmwI6NRdnTA2UeNUmghkVrDSmkJ20s0Vorsx1smrCiUWktT1Vp/+9KfFO++8kyak2Rvtr3/9a6PTwaZL7TZeBPqBD3xAnHfeeQWhu2zHAOciBPrahV92TM0G21vilybXY8f8cSwQ+1d4JYZJQBWsqkLJu1LhkGIV0xeMGmhJpZ3njt2yZcuM95bdTDz33HPDzH3u3GbW0UQ51gmT6H5cAwELAVWwUr4T5nvm/O8RdfG+rCwR4yCegMky/rx6rBNGDY/99BLIAcEqppbEL09MN1c6Qo/6/vGKBAbKogR5vRWbFOcZrELd2BnwtGnTHAWnb37zm0anZN++fYWKCOU2CUj/LFXxpnJlHfQH6iBUmYzw70hgRIKVMqqdajvPVlCvuOKKvHHy7gg4ckGnU6UTJlk6uA4CUQLDEKw80kFwyMZFSDRO7NgS0Km7OmFsI8fJtBA4g2OVD2X0tv4WWjO2iB7kFH3VFN5bSuMTpN7btpsmeNZGQnipoXs/FU+NHPYfpDsWz6PtUyqo/Rf30twxCSKKXJKzMvS+970vecA8DSF9PtC2bduoqamJ5BqzIaXs6uqiiy66iKTqJMkZriHXcaLwCPQfP0ZHw6dkwc+mCRdMp0ka9azwKKHE8QTadq4hzzqjpSepUUDrFyVs6emh0gn0+V2DsXgqG+iFTcWDB2jn49Fajs844wzjONGnXCeMJVIcgEAiAmo/jnxUGbiGzjHCv0snDoVo6646y93S9QeVLppkOYcDPQI6dVcnjF5qCOUGgcwKVt4q6t6/niadPm0tizzu7T1KLz9TR37fBmo1r8rwPRzePMZ/ygSksQ6aMmUK3XTTTfTII4/Y3n/11VdTc3MzSb8RJBd+24bBSRAAARBIRMAiWDV10/rFk2hIU9/XS0e7Xqa6bX7asCva0pPUTDDCJ4of1wYJ6HSqdMKAJwhoE1AFK1+Q+vbeTup42+ljLXTXJ4toe7RKe6m+8zFaPvMs7SQQcJCATt3VCQOeo0cgs4JVSuX0UF1nM62YqVbflCJA4AiB+fPn08svv0wnTpwgaaJ4CJcf/ehHtHr1avrqV79K3/72t4dcxwkQAAEQSEZAFayShVWveyrqqPneFZaOmnod+1YCOp0qnTDWWHEEAgkIqIKVt1oOeJcOHfDubaY1E5YMaicZUZVRe982Lc2iBCkX3CWduqsTpuDAZbDAOSFYSd1cCt5fQYumYrTDjXflP/7jP+i2226jYDBIt99++5Ao+/r6aPLkySSNWJB0vjnkOk6AAAiAQDICqQtWHqqsDVLFqkWElj4Z3dh1nU6VTphYjNgDgSQE4gSrsBSs7HRbjjfvoMlLNkQj81TUU+je5ajfUSLJd3Tqrk6Y5CkhhFsEMixYQTfXrQeZSjzSpxVJh5l06aWX0osvvmh7KwtcP/zhD+mZZ56hJUuW2IbBSRAAARBwIqAKVj5/JV0zO7IK490TFHp4K9VF1YRkDFKdqEeqE0HN24mm83mdTpVOGOcUcAUE4ghoClZ81/4txbRs8+PRCKSFULneEjU9CiTJjk7d1QmTJBlcdpFAZgUr6Oa6+ChTi2rFihX0s5/9jA4fPkwXX3zxkJuffvppuvbaa8nr9dL+/fuHXMcJEAABEEhEQBWsqlv7qHS+qsZ9mloeuouKPr89GoW3sp4e24TR7CgQzR2dTpVOGM3kEAwEiFIQrOj0QSo9ex5F7NJIehXUMXAvzca0tNabpFN3dcJoJYZArhDIrGAF3VxXHuJwImlpaTEs/5WVlRlWAuPjYAtTH/zgB+mNN94gaZ6ezjoLrWA8IxyDAAg4E1AFK6dR6hZpObAoYjmQY/LXtNPO1XOdI8WVIQR0OlU6YYZEjBMg4EQgFcFKxnHsyfto2nXl0di8gSbaf/dQq8TRANiJEtCpuzphohFiJ+0EMi5YQTc37c/YMYELLriA3nvvPXrrrbdsTdDfc889tGnTJtq6dSt97Wtfc4wHF0AABEAgnoCOYEV0nHaunEzr6sy7pZGirhCtmI6BHJNIsn+dTpVOmGTp4DoIRAlIwWqldJtjVFs5QO7Uj4uGp356uHQs3RybtqKa9jCtnmu3Mit2F/aIdOquThiwHD0CWStYMQLo5qb3Rdi4caMhNLGqH6v8xW+sJjhr1ixj5uq1116Lv4xjEAABEHAkoCdYyduP7acF05bF3GpI/4Y90r8hVmE4orVc0OlU6YSxRIoDEEhEoL9N+iP1aPsjNaI6Lq0ETlasBJbVkdi2IlEquCYJ6NRdnTCAOXoEslqwgm5uel+EN998k6ZNm0bLli2jX/7yl7aJLV26lJ566inDPDsbu8AGAiAAAjoEtAUrGdnBh0ppnukdWB6X1XXQthWzdZIp+DA6nSqdMAUPEgBAIAsJ6NRdnTBZWLS8zVJ2C1YSO3Rz0/vuLVy40LAMePz4cVtnwKZp9pUrV9J//dd/pTcziB0EQCBvCKQiWMmWnu4rnkblUeNhPmrs2UtLMW2V9H3Q6VTphEmaEAKAAAiMOgGduqsTZtQzXsAJZkSwgm5u9rxxpjPg7du304YNMX8TZg7ffvttmjp1KrExC/ZvZVZg8zr+QQAEQMCOQGqCFdHpQw/T2ZfcHIvKX0t9O1fBUXCMiO2e2SZzG+206YRxuhfnQQAEMkdAp+7qhMlcCQov5QwIVtDNzabXjI1XTJgwgaZPn06/+93vbLNm+rRycihsexNOggAIFDSBtt1ryLP2QYNBtfRdU6rhu6Z5xxpasmHwHiIP1XY206qZqpn2gkZqW3idTpVOGNvIcRIEQCCjBHTqrk6YjBaiwBIffcGqwADnQnFXrVpF//mf/+m4jorXWD3wwAP09a9/nT760Y/mQpGQRxAAARAoCAI6nSqdMAUBC4UEgRwjoFN3dcLkWLFzOrsQrHL68bmT+QMHDtCiRYuIZ6Z4VgobCIAACIBAbhDQ6VTphMmN0iKXIFBYBHTqrk6YwqKW2dJCsMos/
Question 66xInXXzWRWwt7eXTp48SWeeeWZW5AuZAAEQAAEQSExAp1OlEyZxKrgKAiCQCQI6dVcnTCbyXqhpQrAq1CcfV+5nn32WwuGw4c8KglUcHByCAAiAQJYS0OlU6YTJ0uIhWyBQ0AR06q5OmIKGOMqFh2A1ysCRHAiAAAiAAAi4RUCnU6UTxq38IB4QAAH3COjUXZ0w7uUIMSUjAMEqGaECv378cBs1Px2i1kOvE51zjqQxhiZeNJ0Wzr+SFsyfCVPIBf5+oPggAAKZJaDTqdIJk9lSIHUQAAE7Ajp1VyeMXdw4lx4CEKzSwzXnYz19pIXuL19L5Q+2JiiLlwK1W+lLqxbT+AShcAkEQAAEQCA9BHQ6VTph0pM7xAoCIAAChUUAglVhPW+t0h7ev4NmLRvqLNjxZm8ldfxiE82GuxlHRLgAAiAAAukgoCM06YRJR94QJwiAAAgUGgEIVoX2xJOU9/CjG2nWDVuVUB6qDG6j1TdeTjMmyXmpvl7qeqWZHtpWTpvV2SxfNfXsLaVJyp3YBQEQAAEQSC8BHaFJJ0x6c4nYQQAEQKAwCECwKoznrFfK3mZaOWEJ1ZmhfQFq33M3zXXQ8zu4bwvN8202Q1NJTTvtWT03eowdEAABEACB9BLQEZp0wqQ3l4gdBEAABAqDAASrwnjOWqVs2bGSijZExCpPJXW+sIlmJrnTcg+VUCi8hxY5CGJJosJlEAABEAABEAABEAABhQCMiCkwcmAXglUOPKRRyWJ/G60Z66EHI4kFGrvp7qVTNZI+RHeccQltj4SsqO+ie5dP17gPQUAABEAABEAABEAABOwIwIiYHZXsPwfBKvuf0ajksP/gQzR23ucH0/IEqOuFu0lXPGrbuYY86yIimb+W+naughn2UXlqSAQEQAAEQAAEQCDfCMCIWO4+UQhWufvsXM15b9tOmuBZNxint5rC+0u1Taj3tsh7i2L39sh7YcTC1ceDyEAABEDAmcDp49T2TDOFDrTS6ycHXQ6OGTORps9ZSFcWLaCZU2Gy1RkeroBAdhGAEbHseh6p5gaCVarE8jT88eb7aPKScqN0vqoQ7V2/SL+kx5+klZOvGzR6kaJQpp8IQoIACIAACFgJ9FPLwzto7c3llNDjoD9AWzd+iRbPxAJYKz8cgUCWEYARsSx7IKlnB4JV6szy8o4jj26hGTdELPyVNZDYVqxfTnV9FgQrfW4ICQIgAALDJdB/iHbcegmZ9oZ0oqms66BNK2brBEUYEACBDBCwGASDEbEMPIGRJwnBauQM8yIGVbDyBppo/92LtcvVf3C3XJ+1djC89GcVlv6sMC6qjQ8BQQAEQCA1AqcP05aiWbRZmabylFTStrtX0+WXzqDxZxH1dndR82M/oPK1Wy2zWVVNPbR+MZS1UwOO0CAwCgTUQWqZHIyIjQLzNCQBwSoNUHMxypGsseqX67PGRtdnVVHP/vVYY5WLLwHyDAIgkBMELKPaMseVde1yJsrBh2DvQdrim0ebHzeL5qfWvp00H8uuTCD4B4GsIAAjYlnxGEacCQhWI0aYJxEc20/F05bR4LfXL/1R7dT2R/XkfSvpuvJB/1feygbavykFNcI8wYdigAAIgMCoEIhbg6Hl4iLuHl+1XEdbmsI62lEpGBIBgcImMJIBbhgRy553B4JV9jyLDOfkOO0onkwbIqOavupW+eGdnzxP8oNdPGFJRCAjqgqFaT08BCfnhhAgAAIgMAwCB3evoXlrI+4tpGuMbukaQ8fj4OF9d9Asn+lxsJK6xCZtlxrDyCZuAQEQSJEAjIilCCxLg0OwytIHk4lsqeusiDxU0/oUrZ6faLXUcdq9ZjKZ33ipkIKPdSYeHNIEARAoEAL99FDpWPr8rsHiVjZ006ZiHbFKhu9vkU7gi6JO4Gs7+mjVbOgDFsiLg2LmAAFLHwxGxHLgidlnEYKVPZcCPSsFpZVSUBrU6jMYBOrb6e7lQ3X3Tx9vo/vXeiiiAWiErQ71UOkiLIou0JcHxQYBEEg7gV7auXICrYu00alpCMTfK41YoL1O+xNDAiCgS0AVrGBETJda9oWDYJV9zySzOTreTGsmL4mOahqZ8fopWPY58nxIjoyeOEbPPfETWrc5MmQaya2vukmqDupbEsxsIZE6CIAACOQigWNSZXtaRGXbR03hvbQ4kVJBXBGbd6ykJRH77FVyIAyCVRwgHIJABgmMZI0VjIhl8MHFJQ3BKg4IDolOH2umuz65hLYrpnwTcfFXN9IDpUtJWvjFBgIgAAIgkDYC0sz6gpiZ9fpuQcs1NQE5S20715Bn3eD6LAhWaXtIiBgEhkcARsSGxy3L7oJglWUPJHuy008H9z9C23YEaFednYTlobJAOX1x7Wdp/lTo6WfPc0NOQAAE8peAKlj5qLFnLy3V1r7ulWtiJ0TXxEKwyt+3BCXLVQIwIparT07NNwQrlQb2bQn09x6jo91vEU2YQeNOddOpsyfTjOmTMENlSwsnQQAEQCBdBOLXSaVihVUKVnJ9lrmGFoJVup4R4gWB4RNQ11nBiNjwOWbyTghWmaSPtEEABEAABEAgBQL7txTTsoi335JgK+25XcMtBsd//EkqnnxdxDWGlxq6pe/CFNQIU8gigoIACAybAIyIDRtdltwIwSpLHgSyAQIgAAIgAALJCBxv2UGTizZEgpVQqG8PLdLQxm6WjtyXmGZcfdUU3ltKKdi9SJYtXAcBEHCLAIyIuUUyI/FAsMoIdiQKAiAAAiAAAsMhcEQasJhBmyNLXz3+Gnpq5+qEQtLxlt1SGFsbTayivovuXT49eowdEACB7CIAI2LZ9TxSyQ0Eq1RoISwIgAAIgAAIZJhAb8tOmlC0LpYLX4Dag3fS3EnxtllPU9u++8njK1fCVlOPnK3StnkRuxN7IAACo0oARsRGFbdLiUGwcgkkogEBEAABEACB0SLQIk2nF0VMp5tp+gNB+tz1Hpo6jujYb5+jn3x3He163LzK/yXU1LOHFkOqUqFgHwSyngCMiGX9I4pmEIJVFAV2QAAEQAAEQCBXCJym5t130ZK12/Uy7PFTY/0DtHR6/KyW3u0IBQIgAAIgkJwABKvkjBACBEAABEAABLKSQP+xg/RIcBsFyndR1OOgR2bVXIPlK6Py9aX02eK5pGHjIivLiEyBAAiAQK4QgGCVK08K+QQBEAABEAABRwL9dOzIUXorTDRjxjjq7j5Fk6fNoEnjMUPliAwXQAAEQMBlAhCsXAaK6EAABEAABEAABEAABEAABAqPAASrwnvmKDEIgAAIgAAIgAAIgAAIgIDLBCBYuQwU0YEACIAACIAACIAACIAACBQeAQhWhffMUWIQAAEQAAEQAAEQAAEQAAGXCUCwchkoogMBEAABEAABEAABEAABECg8AhCsCu+Zo8QgAAIgAAIgAAIgAAIgAAIuE4Bg5TJQRAcCIAACIAACIAACIAACIFB4BCBYFd4zR4lBAARAAARAAARAAARAAARcJgDBymWgiA4EQAAEQAAEQAAEQAAEQKDwCECwKrxnjhKDAAiAAAiAAAiAAAiAAAi4TACClctAER0IgAAIgAAIgAAIgAAIgEDhEYBgVXjPHCUGARAAARAAARAAARAAARBwmQAEK5eBIjoQAAEQAAEQAAEQAAEQAIHCI/D/AV2qB3SaJJA5AAAAAElFTkSuQmCC />
If an anhydride is opened with basic methanol
Question 7The reaction in Equation E26.1 shows the formation of only one pair of enantiomers. Draw the other possible products from the Diels-Alder reaction of -phellandrene and maleic anhydride and explain why they are either not formed or are formed in low yield.
Question 8iIwjx1cdur0qLpya/WtQrXGU3bZOU2W60AQwc2dOnVqls+c3ulgh3/fffep4447TpsL4AHBSskXvvAFdcUVVyiYJ6CtN9xwgzriiCNC9vqIFnjssceqao70nc1gMum1PvPaGKzBHv1FhOliLgjABt8K3DP097DDDlNYuU1c+lRzbTAIBuqn/vMoX1uma2SJWyF7nEegGCduFuWWlhY9eTjttNOsTXE/Yc0D6wqMk7ka+0pVILZ8CEsp9Z3pzkVpaO9MIYfIOXObuD8a2ZicgBmYMssKoch0S/l7TqzYLBA2khX4fEIosWspmexcqfaVkkAMAfiYY47R8zefz5cKTV72m0Lxr3/964TXhKUWnh+k38L8Ey6Nl1xyiUIQy0zLn//8Z52T2JrPwkQaGSJgMTlYJalADLMOa9XTVZmdG9jTUhua0Ntaec0TGcuvIl8R36xu4YHCigtWWayHDQ/IuHHj9KoJzP9SrSQhHcaCBQt0MDAI9Tgeib4R4ry2tnZQVlqs/tn9xI8R7f7a175m95CCq4fVtbvuuiu00IFI2oiea7f0dbSoOo7wHgpGx7zICC7gcleoOl8gY3MRu+2Qeg4iUIQTN4su8hbCZC+e1YRVB58//elP9dgBc6tclVIUiP/0pz9prjCLK51iLthDO5yGmU2ExQYpp6WSLJ17mJ2e5kYhxN6Pxhy4Ik8Wktu3b9dCzMiRI1MKHPPnz9e/+1xGIrbuUCkJxKtXr9Zcv/rVr1rdd8SnKRQ//PDDEW2Cgu6qq64KWTFikeTOO++05VIacaL+/2AOjPzDUPBZgjDcobAtVYC3eOfL9rbkAjFfraMp7Jc4cF9i9h3GJB5/5XWOmbhbL/58RHzD6geSVM+bN0+bBlsPBYKWnHDCCeqXv/zlgJKf46FC8u0zzjhDjR07NvTQweQN2xBZbiCrOtl+AHE+tAf9hzCfKw1PLtpt95y4Jz//+c91H3G/YS6D+5BqoSPx+XtUR3ubauEAL13sP9Hais/BW1VL3E7Zkw8CxTRxs3itWrVKj13I+Zqs4GWO1WosAOYy9V2pCcQYs5BtAWMyzKZLp0Tnf0/HGbhH1XvCFjzVdtMClA7cwuppDhRCCAYUspB0Rfsn5w5PeXnQ7QrBjpIVmK8iOFK+LCVLRSDGvB/zPoynqczVk92fXO0zhWLIIFAMnn/++SEzZkQkH0gALvgBL126VGeLsGQeaMtTuULlqr+JzptSIOZwihzNq0HV1dWr5rYBBtfqa1eNdXWqwdes0gz+laj9A96OFz+iosE3N9Pw4MkaAXM+BN9C/kyshFgaXESYmz59uvYBxipMrgqi2N17770KvnVIW2I9jPAlgVAO3zuYQwxmgSk42oVgA8VUIPAizx9W1dA/WABAY49nTooQyBqBIpq4gQl+HxBwR48enTKgxne+8x3928q1NqPUBOJly5ZprkgtWFolMp1ZUzryMIMyXRgqGpwTH6W07mH2eptdhVBkqqV8WRDAbxXzD7hmpVqEx5wUdeGuko9SKgIx4gCBKyw5nVpMoRhtxR/i2qxbty7jJiNQFgLGIu4Rzge3pjPPPJOVOM4cG20IxBmzKIgD4a+LG3Xbbbdlpb0YcDZs2KBuvPFGNW3aNG3yh/NDEIYj+ve//33197//PSvXyuQkWO1HoASsACKNBtqGFUG07dJLL9VR4hDsKV8FAy/YwJ92MH0HstlfPAO/+tWvQqthMFOChthO5PJstkPOVToEimHiZt0tK6pxquiXr732mh6/XC6XdWjOPktJIIbFDhZPMSb39vbmjKkzT9ymqgw3FN8ABOIyb7MzuyitSoNAFhVCfNV2f6Oqq29QzS1ZC8qTtC+Yi2AeinleqlzCCCaLeojsm69SCgIxXH6gcMN46vQ5IIRiLEbjObjjjjsyfgxgaWBqmGHFhaDFgxEoK51OlLRAvGPHDv2QwrR4IFo7RHmGMziCWiEYAR4m/OG8WA156qmnHBmhE4MltNcXXXSR1pJbecSwivPFL35RLV68WL388ss5azuuD801WNXU1KTz3DqyLvoDsxKYxqBPWBXDoFJ6k0pH3p4ib1RhT9ysmwNfN/gNf+lLX0qqzcBvDb6tGLM2b95sHZ6zz1ISiC+77DI9fj300EM54+ncE5spIcvSjNTfp3xVwRyvGP+9Eubfube5RFpmuZ4gT2yqcv311+v5cHTqx1THDWR/KQjEcMXEeFAo46mpKU53Xo5AWbNnz9b9RZ9hHYm4OYWi7CppgRhR0nDT0glshB//u+++qzWAiMAJ31ecA39YVZ81a5ZCyHoI24VW4IOHARSDpxngC6tbyDGGyMiBQGBAiwcmEyvIAEzWMcEt5IK+wAwdzwHM4a+99tpBN0UvZJ7S9tIkcNJJJ+nfECZKyQoWGfFbQ97yfJRSEYhhymZZM+WDq/OuEe1DnI6bWLeqNfIRV/vTVC87D4a0qIAJwG8TbidYYLSrmbNbLxtYsPgJYQnj+MUXX6yQYrTYCnxk0T/EYyikYgrFqQR5BMp64okn1JQpU3Rf0V/L53ggisbB4FWyAvHbb7+tX/xHHnlkSu5YMYM5CXJl7bPPPqGbDpNjaDIQ+AXnK7aCH8XPfvYzhah4puYb36HZRYonmEZkIsxixQiRtPHjgZa6UAt8sJHAHv3Aiwf+0PlcYS1UbtJuIRBNYP369fp39M1vfjN6V8T/4dIBKwyMQ/ly7ygVgdha3ce9KNXSZGh5y2v89jGYEd8JqSodklPSfg+kZhERgIUf5iWpAhPmq8uwlHv66afVOeecEzGPPvTQQ3U70dYRI0aoOXPmqAceeEBh/lnIBcIg5AP0qxDHU/CfPHmythaNdx+w4IL4RKZMdPTRRysEKS7UUrICMTS5icztcKOR7ggO8NBe4oHGH+pPmDBBXXjhhQqmAYW2+jGQhxRC7+uvv64TZuNHArNqiwt8ZJHi6cEHH7QdkdQKMoB0V4VY1qxZo4OkgQE0Kljh7OzsLMSuSJuFgCMIII4BrFEQiCNZ8XqDmQ9giZOvUgoC8R//+Ec9pp966qn5wurI63T7q0PvNiK3shssOhztnecLZdVK9MOOvL0l0ShoWzFHg4Y4l9H3k8HE/Ph///d/FVwwMLZjnoT5EhQHcMn78Y9/rN544w09j0ZUY8TdQTwI7LfmlhC2IED/7ne/KxizW4sJojWjH7AkLdQC+Qf3w1R64f2Me2cFysJ9RdpYpwbKSod9SQrESIqNB/Vb3/qWZgVHd5g2YCUNuS+tHy7qYEDBBAEBXiAoSwkSwCCLCRQc5/fbb7/QAAZmMLc+66yzNLN4EbS3bNmiA3phwE41+XUabyyEYEEA/cQCCZ6hVHlSndYHaY8QcBoBa/IAt4xUZe7cuTr6Zap62dxf7AIx3oFw+YDVUy6yLWTzXmTzXHgXxab+MP2IWbj11KUUbrsDdRHvwIqG4jP/zCZ3OVduCUBBgTkK0jvmq0BoglBUVVWlM6hgcRNtwB/GFmQEeOGFF1LGpMFYtHbtWoUI9wcccEDoHJiXQ7D+wQ9+oAVtmOo6tSAwIYJTQZh0WprTdJjNmDFD88c8HtagyExjKcPgGoggwfk0s0+n7ZnULTmBGD+i8ePH69yVmHwhMIsVbRk/XERDw0MA3wb4CkuxR6Crq0vVckoh5FKG2Ys1EOITptHf/va3Ffxs4TeCfMjYDvPiQikILobI3Fa/Tj/99LwE8ykUPtJOIZApAUyAEH8BQQjtajPs1su0TdZxmMxgXMM7ARMyaDuQJcBcMbfqFvLnkiVL9Nh2ww03FHI3bLcd76srr7xST1hh4RQd86M7UBMa6/WY7/aqQFc8E2gOZtcQtFiw3g3QDie3cbDdTKkoBNImYCl8oNzJdYFCA5aBMHM203pCGIRmtI7TrEb/ttJtE8ZgxLaBFhIKKut3BoEbaYGQIebNN9901Ji8cOFC3U6nmKuny9yqj4jj4A05yeKOe3v77bcXnMbe6lOyz92wkztaMoXzwhKnF8JCAPGkhniSQ5wfmFgLTBxtmdjmn1jzVzI8ctFRsOXIr8QRl4nzgxKnoSJeiAhdin9QxJNg4h8Z4Tv+OBqd/hszZgzxxJj23ntvYsFa//FAqz95RSrv94Ynv/q5YB8Q3f7jjz+eOME48csm1B/5IgSEQOYEMB7ff//9xGZxdNppp2V+oiwciXGKNYbEGmtitxlqb28PnZW1FcRp6/T/eeGUOP4E8YSBOLYEsWlfqF6hfWHhkFiDQ5wWhHiCm/cxNp+82I+ROAUe3XzzzfThhx8SazuINVH005/+VPffbMv6ZfPoqEseNTeRp6qGzp19NI35LFHnWwFaed98Wv68WcVNTR2radYYc5t8FwL5IYB5FfvkEls+EKely/o8Bb8ZdhejRx55hF588UU9XqBnmJuxuTOxZSCx8oPYajBnHWaLPGLNN7GQTJxKijiOhL4W5okzZ84kttojDgyr55E5a0SSE7MmlTjAlJ7Xsva0oMdTTtFKnClF95bNp4kXHzRfyE3FWEpKIOZgR1ReXk4Qcr72ta/R/PnziX1YiVeaivHeOqZPGKTZl4R4tZAaGxv1JAQCc7oFCxVsgqLvFyakHFSH2I8hJDjzSj/xCmKEcI3/WwI1BGzzO45PtPjB+ZG1INzc3KybyT4vxLmFiVck02221BcCQiABAbbCIbbY0b8rjBGDUTggIv36178mDpyoJ5Hm4h2b6BFrJohNEAljAMaDJ598kv7whz8QxwwINRcLeBxokDi+BLGVjB6bQjsd/oXNwfUCAAe80QvDDm9uRs1jf0b9/rnqqqv0fcO4z5ZKtGzZMr34Gv+ku2jdw1fTzPn3xN8ds9VDvrZqmnPg0Jg9skEI5IMAp/8k1k4Su5Xo8Wyg18RYyNZxobkbxkooPCAQceRkOuWUUwjjB4ThRHOpgbYh2fFQakHhgvEbC6pssq0VXTgGi5SY32POP3v27JgFr2TnHcg+zpRA7E6o+eM+FHJ5/PHHidNGEecQJg6iW8hdsdX2khKIsfqNFWH2cbUFRyrlhgAmJ1hp/OCDDxL+sZkMYXUN2gssZOD/7NtGbH6jj+Uo1YQ/rA6y+WSEBjqdVmMxBMI1m80TBGoIzZigQ3BHwXdoidiUUGsV0jm31BUCQiA5AQiRHJWSOKgKHXbYYckrZ2kvxhFMnjCJ4gj3elyxTo0FNDb105pqWINwNGtrV8wn55/XWmRMGji2AHGMCV3HmixCS8F+c3qy6NQVdWiR2BVEa7v9fn9MHwt9AybvWLxgU3fC/UJh805iM3iCxt9O2dW5kVbVLiPv4nsoYB3g4i/9/3G5K2jx5RfRmXOmkojCFiD5zDcBLNDhmcb8CnMnzGfSLfi9QBkAyz5OpUOvvvpqaG4FAdNc9HOiIgnzQfZT1sqL559/nrDgigJhHQI8LJBg0cPRkLVyJV0+qepj3ghrU4ypnKI0VXXH78eYiUVhdi/RVjSOb/AAG1hSAvEAWcnhDiaAgRzmcNFCNoeO1xoBvCwgXFsCtiVcQ8B+5513tNCNyTC02VgVPeaYY2jRokV07LHHaq0yNMN//etfHUxAmiYECosABGGO9q+FxocffjhnjcfvGdpnXIPTpOnfu3UxTOo4rZzWFp544ona1C0TTQc0FbA84pz2ejKJyRAmpigwJ5w+fbo2NYNJIcdUsC4/qJ8YM9F3aICg+bErIA5qo9O4OAR8Dvqi+4fDMIbjGYBbVGallzq3bqP3u1n7NH44dXXspL3G7kOjR4gYnBlPOSqbBGCdAiu2m266iW688Ubbp4YJMsYtDhyrx0lrYQ/WdF/+8pf1uAXXkFGjRtk+p1MqYr4Hy58VK1bovmF+iAIFCLTanOKP3G43caDUAWu4oZjBoi7catinWQuSTuGQaTvw7gQrLO4+9dRTmZ6mcI7jl6IUIVDSBBCJkX+xOmp2PBCIos2T5IKOFhivX7JNCAwWAQSlQuRR5BLORd5uXtlWd955pw66YgZNxO+c/bt02gj2gctZHmPkWUdqNgThOqg/TzmujT82r9ZR+BsaGhRP0AbrFig2/dbtQcDDYiq492zKqfsG3jxJ1VFri6mP0hchYBJA0E8868jwwQtx5q6Y7whsylYtegzCWGSNSxgnkfbouuuuU7xAFnNcMWxgVz3FCwZq2rRpEcF0WfhXvCCqHnroIcUWgRl1leMQaJZsYpzR8U49iBeNdT5lp7Yvm+0quSjT2YQn5yoOArwKpiPIclC1uB1Caim8NHiFLO5+2SgEhEB6BNgfSf+m2OctvQMT1LYikfJKtk53YU3y8Ino1RD62ARQR7lPcIqcbmZNhU6Bggj7HEAwNAnFQhsHdVSISopJbarJbLYaydY0Cjk+sSCRr4jd2Wp7ovMgDzxryfTiJe47shtA6MfiixQhUKwEMGZwgL+EcxT81rE4x8ELIxbnMPZwoCSFlHJIJ5mvsccp9wHzPqRcQ3oncAAP672BdwZSamLR0s6CLTLSYCxFKiLwLqaCRRMstJRCEYG4FO6y9DElAWhxMIGKV9gnRQ+U0PZIEQJCYGAEkM8dkwdoiDEpyaSwa4Ni/9+4Glicm/1/VU1NjWM1Hch/y9GOFbtk6FR/1kQMEyp211AcyV6hTq4K0mbgmvfdd1+uLpG383I8CrV48eKQxgcLDrWcKqvUJvh5Ay4XchQBjoWgf8vQeqLguWd3Aa0JhcbXyhuL3zt+G1g0hFUcrFikhAnAWgeac6R3il60RP7jiooKlciqiAP06nuAdK3FVmBRhcWCTN/VhcRDfIh5lJAiBDweDz3wwAP0r3/9KyaQDvwD4QeIAFttbW0CSwgIgQEQQKApBLRC0BNE/7Rb2IyPOJe5TueGdBvw2UJBwCpEgEbUYESERjokBE8slMITBh0pFVH44af1xhtvhCKlIgAkIqWylQohyFcmgXKiOWzbtk37CyNgGNKzFGrhCRr94he/oGuvvVYHWkTaqKqqKvrhD3+o/d4KtV/SbiFglwBioPBiPrEZtPYbxpiKeAkIOIrCi4PEgrKOFIx0SIiGL8UeAQTk+s1vfhNK74QYNSjIdAKmiAeBAFp4DyGFKFJNbd261d7JC6gWYmsgBSF8zTEHLupSSNK7tFUI5IoAB8zSK3zQLMQrWGnlgUDxgBdvt2wTAkLABgH4pmG1maOVpqwNM2iOdqpgZswB7/TvD79B/MGaAy4OHCRLQUNYTIUjpep4BpwuRPfT6jO4wbz6Rz/6kdaOQ0ueSeEoq5rhunXrMjl80I+BCTRPVLUvNtjAx62ysrLonoNBBy0NcDyBq6++WluYsJCmf9PQBn/hC1/QLhivv/66uAtk6Q5izOGI23rsBV9T6w7tMcYhXozI0tWcdZoFCxbo/sEiq9iLmEwX+x2W/tkigAEPEyvOIRq3Pkdt1IMCJ6SPu182CgEhkJoAR/rV/vrxzIEtM2j400LwswRBfCLoCecCVhwlWMFfq5QKfNjQb4xNrCEOccF4BfNq+GMjWIydAlNK8GSts53qjqsD95WDDz5Y94EtAxQma5xJwHHtlAYJgVwT4FR1OhDUoYceqrDIxblvVaaLZLlua7GdH3EXnn32We1nDJNijMXx3mnF0G+47+CdsWrVqmLoTtI+iMk032kpQgAEYGq5adMmnes4Om8oQulz4AVtlon8fFKEgBBIjwBSHnH0X+LgLtrUFUezxpiefvppnfIDac0sM2iYPCM9DtJinHnmmRmnQ0qvhYVRG6Zrv/zlL3U6EdYChZix35vOscvBYPTnnnvuGdEhngnoMQ65RTs6Ogj1C6UgXzJrzOmVV17RTT7nnHPo7rvvLn4TvkK5QdLOvBPAnAS/YaRHkjJ4BOD+AzegYk3NuXbtWp1/+mc/+xmxddLggc7DlUUgzgNkuURhEID/GfL3YdIFH5HoYk0w4a/D5ovRu+X/QkAIJCAAP3z4rCLHJYQ5NoUmn89HyBNulQkTJhBrgWnevHk0c+ZM4lV3a5d8JiAAIRcLCYh/wBoi7ROMbSisZafTTz9dL+LNmDGDsJDHmiS68soriVOEJDijszYjpgMEYY6SqxsGf7Z7771X5/t0VkulNUJACJQiAbzbkGceeeix6It3WDGV9957j8aMGUNsjUMcqLKYuhbTFxGIY5DIhlIlgMkX+ybSDTfcQDfffHMMBgRQaGxsJDZVIvYjidkvG4SAEIhPAEIwAtdxrkuygpOMGjWK2ORXCzz4bVkLTvHPIFvtEGCTSeJUIfSrX/2K2OcrtOCAxQUIyAgKePjhhxPYs1+21jAh0A7+sA1/CNwV/R3BefK5CIhgQRdffDFxNFy4ddHRRx9N999/v9bC2OEgdYSAEBAC+SKAQGZYdOR0TYRgXPkcK3PdR4y/sNhCcEcsYhdzEYG4mO+u9C1tApgIQlMFs8LogoiDMEcsBdOR6L7L/4VApgS6u7sJJq4wvZo8ebI2g8bvCNFRpeSWAKxZHnzwQa2Rhzk6TKwRnZlTs6R1YUzwIFRDMMYfIjrDVNMSoCFcIyI2/qBN4BzHWti2BGt8jhgxImX0bwj07EOuhV/LqgDRt+fMmZNWe6WyEBACQiCfBGDJgrGKU9oRB/nL56Vzfi2M9Yii/eabb+b8WoN5ARGIB5O+XNtxBDhwjU4HAw3F8OHDI9rHUW+1Fgsh9jlCa8Q++Y8QEALxCeAlit8OzMqiffPjHyFbc00Awibn3SQsVuCPA3dpzUZnZyfBRA6m7F1dXfq+4d6hDkfz1n8we4eWHwI2BNh0CjQNsBKAcD106FD93RKqoV2BBgLXgXk9NC0QhItdK5EOP6krBISAMwlgvMIiLzSqGDuxaFgsBUoivAPwLijmIgJxMd9d6VvaBDiaK3GSdW0affLJJ8ccjwEPueYwKUQ+OilCQAgIgVIlgMkfBFhLsDY/IVhDwLaEawjd+MNiI/7gogKhHMIxBGuciyPm0qJFi+jCCy/UljqYWKIu6kgRAkJACDiZwE9+8hNavHixtoKCu0exFLisIFYFpwQs6rFYBOJieWKlH1khgAkaTPtg/sIplmLO+YMf/EBHyG1ubtY+IzEVZIMQEAJCQAikJAAfZ/iQX3HFFbRkyRLq6enRi4yW8IsAYCtXrqQXXniBjjvuuJTnkwpCQAgIgcEkAKuZQw45hNrb24sq1gyyPSAQJrJCQClUrEUE4mK9s9KvjAmMHz9e+9jBBCa6WCHoL7vsMh3tNHq//F8ICAEhIARSE4AvM8wKYY7X2toacwBMpeHCcu2119Ktt94as182CAEhIAScRgCBVxEkcurUqRQIBJzWvIzac80119Add9xBTU1NNGvWrIzOUQgHiUBcCHdJ2phXAhdccAGtWLFCr/Ih6rRZsAJoTeLeeustc5d8FwJCQAgIgTQIfPWrX9XxGOCbBsscs8CEGtpiRPSPF+TQrCvfhYAQEAJOITB79mx68cUXda74uXPnOqVZGbfjscceo/PPP18HDcNnsRYRiIv1zkq/Mibw3HPPEfJdLl++nL73ve/FnAc5UhFmH+bV0YG3YirLBiEgBISAEIhLYOnSpdpk+vHHH6ezzjorpg5SRCHNHfyQEclaihAQAkLA6QQQSBIZFZBKcNu2bQUfb6alpUWn67vlllvouuuuczr+jNsnAnHG6OTAYiUAUz5EQIVpyPPPPx/TTaRduuqqq3SOTPhWSBECQkAICIH0Cbzzzjt0wAEH0Omnn67zJ0efAQG27rrrLnriiSfojDPOiN4t/xcCQkAIOJIAYiNgwa8YXD4QOBGpl2A9+eijjzqSdzYaJQJxNijKOYqOAFb3tmzZoiOoRqeKee211+hLX/oSnXbaafS73/2u6PouHRICQkAI5IsA8hZjERI5k6ML3FImTpxIF110ET300EPRu+X/QkAICAFHEkB0fMSjQYo6xKPZa6+9HNlOu41CujxEm37ppZfsHlJw9UQgLrhbJg3OBwFogKEJ9vv9On+qeU34tsF8D4Iy0oJIEQJCQAgIgcwInHvuubRq1SravHmzjtAafRZoJuBfjDRNUoSAEBAChUKgtrZWL+Z94xvfoKeeeqpQmh23nRDoMQ5DUVSsRQTiYr2z0q8BEUAQF0QJ/PGPf6yj60Wf7Oyzzyb4vWHlb5999oneLf8XAkJACAgBGwSefvppwoQRUUwx3kYXpFxCdNNiT/kR3W/5vxAQAoVN4JNPPqEpU6bQpk2baP369XTkkUcWbIcQ3BAuLjt37izYPqRquAjEqQjJ/pIkAC0wAmYh5xoCCkQX5Cj+9re/TVVVVXT99ddH75b/CwEhIASEgA0CmGBB8zBt2jQ9aYw+5P7776dLL72UHnjgAbr44oujd8v/hYAQEAKOJYAArDNmzKBDDz2U3njjDdptt90c29ZkDZszZ46OqYPxetiwYcmqFuw+EYgL9tZJw3NN4JhjjqHm5maCLwhSLZkF5ntIyXTEEUfQ3/72N3OXfBcCQkAICIE0CCCaNCKzYrIFXzWzYPwdOXIknXzyyYQcn1KEgBAQAoVEAAEBV69eTb/+9a9p3rx5hdT0UFuxGIk4DtB2Q7gvxiICcTHeVelTVgjcc889tHDhQu37AZO+6HLIIYfoXMUfffRR9C75vxAQAkJACNgkgEist99+O73wwgsEE+nost9++1F3d7denIwOchhdV/4vBISAEHASAbjWIZo+NKv4Xoga1rvvvpuuvPJK8vl8BG1xMRYRiIvxrkqfskKgvb2d9t9/f0LQl9/85jcx54Sp9MMPP0yvv/66NvmLqSAbhIAQEAJCICWBDRs2kMvlShhN+rzzzqOVK1fGDXKY8uRSQQgIASEwyARuuukmuvnmm3XedShbCq1AED7hhBMIgcIuvPDCQmu+rfaKQGwLk1QqVQKIrLf77rtTR0dHqSKQfgsBISAEckoAMRvgR7znnnvSP//5z5hr/fGPf6STTjqJbrnlFrruuuti9ssGISAEhICTCXz88cc6DRPSy7W1tWlli5PbG922f/zjH3TggQcScsN7vd7o3UXxfxGIi+I2SidyRaCiooJefvllWrNmDX3mM5/J1WXkvEJACAiBkiYA7QO0EFh8RG5isyBP8dChQ7UWGdFapQgBISAECo3Ak08+SW63W5scY6wrpIIxGHmV58+fT3feeWchNd12W0Ugto1KKgoBISAEhIAQEAK5IAD3E0y2fvnLX+rP6GsgfQkCbyHIViH64EX3R/4vBIRA6RE46qijdDR9pJKbNWtW6QFwcI9FIHbwzZGmCQEhIASEgBAoBQLvv/8+7b333gm1JzDVu+uuu+jZZ5+lE088sRSQSB+FgBAoMgJY1ENO3wkTJujc6hIk0Dk3WARi59wLaUkBEOjcvJ5eXPsnatn0LvVwe6GpGDV2Ah12xEyacdRkGr17AXRCmigEhIAQcCABBDGEj90HH3wQk69z48aNBC3x97//fbrvvvsc2HppkhAQAkIgNYHvfOc7OgXTvffeS5dddlnqA6RGXgiIQJwXzHKRQifQu2Ud3XXFTLqhIVlPXFRZs4QWfncOjRHBOBko2ScEhIAQiCFg5bp85ZVXaNq0aRH7EXgL+eChRUaAFylCQAgIgUIkALePffbZRy/6bd26lUaNGlWI3Si6NotAXHS3VDqUbQKbn/kJTTplcRqnrSB/1xKaPjqNQ6SqEBACQqDECaxdu5a+/vWv0zXXXEO33XZbDA3sQ514gbdiKssGISAEhIBDCSxdulSnYPrud79LDz74oDNb2dtJ6196kf701xZ699/aJpKG7TmKJhxyGM08ZgZNHldck1wRiJ35GEqrHEJgy5PX0EHuO4zWuMhbfy+VH38EjR09gqh3B7W/+QqtvPdGWrz8+XA9l5fa/76IxoW3yDchIASEgBBIQqCvr4+GDx9OkyZNopaWlpia999/P1166aW0YsUK+ta3vhWzXzYIASEgBAqBwCeffKLTGLW3t+uxDn7Fzim9tG7FXTTzghuSNsnlriTvnQvp5MmRWQGSHuTgnSIQO/jmSNMGmcD2dTRnr5kUEnPd1dT6yOU0keXgeGXLmqV00PFXhHa5q/20+vLpof/LFyEgBISAEEhOAFFYYTLd3d2tTaTN2tAMw9TwG9/4Bj311FPmLvkuBISAIwnsoi0bAvR+X+LGDRkynIaPHEljx4+jESXkbmZZxMycOZP+8pe/JAaUzz29G+kn502hxUndAyMb5Kn107ILC3+uKwJx5H2V/wmBEIF1S+fSzCv6RwVXFWt8r0+p8d24YgFNuWB5/znKqKlrDc0qLquSEB/5IgSEgBDINoGf/OQntHjxYi3wQvCNLmPHjqWPPvqI/v3vf8cE3oquK/8XAkJgsAnsoKXTRtIVAXvt8Hjr6dYffbNk4rAcd9xxhBRMWOCLN97Zo5alWrs20zVDJlGETaTHS/cuPJeOOGi8XqzYsb2dXnlxJd149uKwsogvX+Vrp+vnFLZNpAjEWXqO5DRFRqB3A80b5qJH+7vlbeqgRbPsmIVspVumjacb+gf/ivpWWvLNiUUGR7ojBISAEMgNgbfffpsOOeQQOuecc2jlypUxFzn33HNp1apVtGnTJjr00ENj9ssGISAEnERgBz08dyTNT0PjSGyN17H6crIz43JSTzNpy7/+9S9CdP0xY8boYIF77LFHJqfJyjERSiA+o7exlRadnGD+umsLLf3mQWTpjIjc1Ny1mmYUsAJIBOKsPEZykmIj0LtxBQ2bckGwW+wP3MH+wHYH582sJZ5kaYnL66jnkfNpaLEBkv4IASEgBHJEYPTo0fTpT3+a3nvvvZgrvPjii1RZWakD0Rx++OEx+2WDEBACTiJgCsRlVNN4Mx3+WaN9fR/Stne30PrGlXTHoyEHNXLXBGj1gqlGxeL96vF46IEHHtCBBBFQcFAKuwjOZRdBa93ClsaXFUcLWHEUson0NtGaRbMGpfnZuKgIxNmgKOcoOgI7Niyjka5Lgv0qq6HuNQsogetwTN97N7MwPalfmE7z2JiTyQYhIASEQIkRcLvd9OSTT1JbW5sOPFNi3ZfuCoEiImAKxG7y96ym6Qk0BOuWzmM3tX67PDfPu1bbn3cVMjBYw9TX19OQIUO0lnjffffNe3c2PjyPpszvZ5+GEmjrmlto/PFW8K0Kau1bQhML1A9cBOK8P3ZywUIgsH3dUtprZjBAlru6mYNjzbDf7Ahz60oeIG4v2AHCfqelphAQAkIgOwTgU7dkyRL9d9BBB2XnpHIWISAEBoFAlEDczQJxIu1C73qaO+yooJayRJQJiKYPS5cJEybQO++8k9BVJLc3rpdWzBtGF/TLw1W+DvYHtmkTuWsjLRgyJaQlrmvpofMnJ1jxyG0nBnx2EYgHjFBOUIwEtj7Dq16n9K96VfpI3T7Hfjd5UJ/Hg3pwbGG/Cn4BzEj0ArB/VqkpBISAEBACQkAICIECIpCpQFxNXWsupwJ2SU15j5RSNHXqVHr99dd16iUE1WptbaXly5fT0KFBoRJ1dtttt5TnSqfCZz7zGS14h4/ZQcvYz/uSfnvpan8XXT7dLvleenzBMDq732662t/NxxbmhFcE4vATId+EQIiAaQZSlq5fxNZnaM74U4IR+Mo4OAQP6jbX2kLXly9CQAgIASEgBISAEChsAqZAXE6BvkdoalyT2l20bun8sMl0RQP1LTmd4lYtbCCh1iNo4HnnnUfl5eX0yCOP0IYNG+jMM8/UQnGoUg6+ID7Dxx9/TJ/61Kf6z95JS+eMpSu0C7ebs6OsTis7yoZl88h1SVAFVNHAgWRPTxCIKwd9yeYpRSDOJk05V9EQGJAPMfsfDzP8j7vY/9juWlvRAJSOCAEhIASyRaC3k9a/9CL96a8t9O6/e/isw2jYnqNowiGH0cxjZtDkcTLCZgu1nEcIZJeAKRBzep76RvraXntogYwQUfnjD6jr3TZ6efVDdE8Dp+dw8dUDZdTY/iydPK54xeHe3l7ab7/9CJ/btm2jkZyHGSUQCOjYCf/5z3/opz/9Kb300kv0ve99j0455RS9Pxv/fO5zn6MTTzzRONUWzo5yUCg7iq9L0Zw0hlRTIC7zNnNgrTRcDI1WDPZXEYgH+w7I9Z1JoHMNzRl7fH+etXLydz+S2O8lqgfrOTDEUf2BIVxsbv33dMyto84l/xUCQkAIlC6BXlq34i6aeYEVtCU+CZe7krx3LqSTJ4stTnxCslUIDBaBSIE4aSu0MExU2dxFtxdy/p6knQzuvPrqq7XAe88999AVVwTj1ZiHvfXWWzRp0iSdWu61116j3XfP5eKAmS60jJo61pCtLKO6wbtozS0n0fE3BCOE209RavbWGd9FIHbGfZBWOI7Adlo2Zy+6pD8LgLvaz4G1pqdu5Q4OCjGyPygE1/bywL6oyAf21FCkhhAQAkIgTQK9G+kn502hxQ32j/PU+mnZhTbGafunlJpCQAgMiEAaAnHoOi6q9T9HF04vzgUuBM86+OCDtYZ4y5YthulyCAAdeeSR9Morr9ALL7xAxx13XHhHTr5F+xCn4wcceX/T8z/OSWcyPqkIxBmjkwOLnYDpRww7ntrAC3Th1GR2JNtpxYLZdMFyNvvRpZLaOML0gblc2Cv2myD9EwJFRmDHlg30+vt9NIT4b9RhNHVisjGlyDpvtzu7NtM1QybRHUZ9l8dL9y48l444aDyN4DF1x/Z2euXFlXTj2Yv7LXmClW3lzzTOK1+FgBDIJQFTYCqj+ub76MhRxKNfuOz8v056q+Uv9Oj8xaE8uJhzNbT76fQiNJuGufJzzz1Ha9eupWOPPTYMov9bY2MjnXrqqYT0c6tXr47Zn4sNa2+ZQ1/v1/KW1/jpkQU2FxZ3cP7ikVb+YhebuvsL19SdI5hJEQJCIC6BblXrJsWDT+jP2xBQfXHq9nUFlDe6bnNHnJqySQgIgdIl0K6qjPGEqEK1lS6MhD1vrnaHxlyMv97G1oR1VV+bqo4Ye92quStxddkjBIRAPgmY8yi38vckuXZPq6oqC8+3XJWNcedbSc7g+F2s8dVj2+zZs+O29ZNPPlFjxoxRnJNY/eMf/4hbJxcbu/3VxpjL96nb3lX85lhdVq0Keegle12WWkKgRAl0+1V5xASWB+syj6qpb1R+f0D5m32qtspjDCTBwZwjU5coMOm2EBACiQj0tNTGjBXsc5Woemlu72pWbmPMZY1vag49AeUxjpHxNzUyqSEE8kMgSiBOIWh1NxuCWYELWNF8+/r6FOcbVhzlWXEgrejd+v+33XabfkfceOONcffnbiMv1rrCixHkqUsp3HYH6iLeZxUNhb28KwJx7p4uOXOREOjraFYV5kBhTLxM7bH13VPdpJItghYJFumGEBACaRLwVbp4AoG/4MSDY8goKq+T8cLg2FJbHuJDLq+yu1zQ7qsKH8ea99Z4pjzGdeSrEBAC+SCQnkAcsWhYVpNSKMtHD7J1jSVLlugxauHChXFPuXPnTsU5grWGuKcn/7PI7kCNMYbyu8ntVYGueANpn2pp8EbW5cULu2N13M47YKP4EPPMREquCeyiLRsCxG5zREM+T66pBxZgbrle2rjmCVq21BtMDRCDzEUe72L6QfmZNHVcMKF6TBXZIASEQOkS6F1P84YdRY+CgMtNbvaWQ5aRYvaVQ+/SK720Yt4wukBD4hQtvg66fo7NwDq7NtKCIVNoef8F61p66PzJMhanx19qC4FsEzB9iN3U3L2aZoxIfI2NKxbQlAv6f8XlddT9yPmUpHriEzlsz/vvv0/7778/scBLnZ2dxCbRMS0899xzadWqVfTb3/6W5s6dG7M/HxvWc07ho/pzClvX81TV0Lmzj6YxnyXqfCtAK++bT8uft/bik3MXd3DuYptDtXmko747QCiXJhQ9gW5VbWlYXU7wMehRTbWVqqo+iV9aknvS092h2lpbVFtHl+poa1Vt7V2i4UnCS3YJASGgVHtjZWhF3V3drFrqK0L/59yNgkgT6FY1hj8wRyxNg0uPqveETf6q7TrBpXEFqSoEhEC6BKI0xPEUjvqUPaqlMVLr6K4JpHsxx9afN2+eHu9XrFgRt42tra1qt912U0cffbSCH/HglT7VXBt+N7HAGnpPxf/uUb62/Guzc8FHNMSOWp4o1sYYK4TuGupevWDwVvw4euktR03SCcjLOJXSGjuplIr1tki/hIAQyBOByLQWNYE+WrDvczRt7CkUjEnvoZa+ZTS55CPSd9LSOWPpiudxW1jr0MVahzSCcG9g7YarX7tR0dBKS06fmKf7KxtiLqoAABWESURBVJcRAkIgPgFj/scVXO5ymrnPcKPqTtq5bQcFGhr6x0Jrl4cCPctoahEYeSB9EtIoTZ48mVpaWqwORnxOnz5dp1lCzuEpU6ZE7BuM/+zq3EirapeRd/E94fvSnyca7XG5K2jx5RfRmXOmUhHcIo1YBOLBeNJK7prGgFjGAvGaQRSIjTzBtnMLl9z9kg4LASGQTQK7tj5JQ8ZzqChdqqhdXU/jyBgXeXulr51unzOuv06pfmyhW6YdpBcsQcDXpWhOhgIxa91pzaIZpQpS+i0EHEIgcjHQXqPKqKGlgU6fXPjG0qzJJEvYff311+MKu7///e/ptNNOo4suuogeeughe4jyVquXOrduo/e7ifYZP5y6OnbSXmP3odEjikUMDoMUgTjMQr7ljIAx8Rtsgdjw4xOBOGc3XE4sBISAQWD90rl01BUNegubAdLqBVP194hc52w908XWM2nIf8YViuXrVhaIx/cLxGXsl7YmDb+0XbTmlpPo+P5cmhy9mxYVvFNbsdxX6UfpEuilxxfOoLPvCdrCJOLgcpWRa+ZMOva0U+jMU2fRmCKxlnnsscfo/PPP1z7B8A2OLmweTfvuuy99+OGH9K9//YtGjhwZXUX+nycCpSUQ79pBGwOv0KZ/bg/i3eNzdPCUI2nqgfGmIL20vXMH7ULN3UfQmNFxVkN6t1PnDl2D6wzlOlGrWbu28/VepTa+3sc4T9LroUKysovbs123Z/cRYwjN6dy8nja8+U/6gE++x+f2oSlHTqMD47WTjwoeuzuNGTOaOjeuo79s2sbHjKZDpx5NE8dE9W0A7e7dvoX+/rcW2qYbNZoOm3IETT5wCD08dxjNx3wwQiC22sXb4/Hrx9G7vZOAefeho3lVKv4ouaNzM72+cQtt2/6BPmr0/ofREa7JZFbfsZ35df+N5h90vE7+Xub10f98/0ja1Us0mrnEP3N/I+RDCAgBIZARgc20cLdJdI8+1kWN7X46eVz/aNO7gQNtuYKBtnh/fWsPfXNi1Hic0TUL9aBIbRL7AdPl06Peqwm7Ziy8ch32P+Zj473bE55AdggBISAEskbggw8+oAMOOEALu9t5/jl8uGkqHrwMp1mi6667jn7xi1/QpZdemrVry4kyIJALx2QnnrPVV6PKEjiHu8oRWjyy1a31Zm5Zl/LFxBNvi8zZVV5vBFbqUc11VUqn1IhzTVzP35EwskBkQ6z/dTeH2u+qqFE1FWVxHd3Lq+pjQp+H+1Kmqrxmv4LO8jUBKzHcANrd167qKt1x2+Su9CqPFVSLw+hbV1NGnyhBsK2e1nCeM1ecwDM9bU2qqjycxoR/AkYbylR1Y6A/sXtXOLBXRB3UL1PNoUZZwOVTCAgBITBwAl1mXs04KZaaqsJjuatK8pebPMpr/PZvAL9PwvmLXaqxPc13rP0rSU0hIASEQEoCV199tZ6P3nrrrXHrdnd3qz322EMdeOCB6j//+U/cOrIxfwRKIg9xc42R1zBGGLIEKLfyRbxA25XXEuJwjLs2LMjx/WnyhicxRB7VEgqy1q3qKxIJaNa18OlS9S1pSGE9flWesO3mefk7T7rMMwdqIKiG2xQpqLtVk14MGEi7uyIig0YKpUbbwNMUiM0+uQ1B2Xj+zbxobOJs7OGv7b7QIkHCazIzj44mHRmBNLK+CMSRYOV/QkAIZIdA1LhT2aja29sUIorqv7Y25a8PR58mKlf+0LskOy0otLN0+6v1JDI4RruV3WDR/mpjQZZzYkatcRcaBmmvEBACBUwA4/unP/1pNXbs2IRRo8855xw91v35z38u4J4WT9OLXiA2BSq8YMureULSHVw57m5rVpVlhsAWlQS8r60hQsvLUSv1nY9Y8edz1oY0rEq1Gak1cD1PjU919OB6faqjxRfWlPI+DqOi2uw+S6bw2C+oV9Q292ul+1Srz5xEkKrytYfOHIheEHB5VG1Dg6phja6rokFrUAfS7rYGc0JHystaWT2n6+lQjdXBxQiXtbiQSCA2t4darpR5/yIF4mgh3KMaWzp0X/p62lVDlTE5CnHuU12t9aHJFptMq65uTp3E6ZNEl2BAl69CQAhkh0BXk61FO3OBrqLB9lshO2103FnaI62vPHUphdvuQNiSCCyFoeNuqjRICJQUgZNOOknPNZ999tm4/d60aZPef8IJJ8TdLxvzT6DIBeIuVVseFnjjm1+1q2pDKI7Oe9hq5IrE6n1TS7PyaGE2eN7y2oBx19pUpbGvIl6e254WVWHUqWy0OfkxBWI+PvK6wSa0+6pCwh65vCHT6UiBuMLQZltNH0C7+1oj+sOBTKyThj79pkBuCr5mn8ztoSMTC8R9hik1NPSxWgQz9x2pUE7KnkBI0x4pYBsXla9CQAgIgSwQaK2LdVExhd+438vCY3cWmlCQpzAXQjUjN9ya4i1b9qmWhsjcpcTa4di3UEFikEYLASFQgAQaGxv1XPzLX/5ywtZPmzZNa5DffffdhHVkR34JFLdAzAJXyKfIVaXCOtNIyF1NYUGSc9NG7mTjY1OojpjARJlRqw7DhDfJ9dobw9dzVTTa006awiNMtOPNDbiHVSFh2x3yizUF4niC9IDa3W0yTjCRM++DKfiafTK3G3fAnBiZAmxLbdgMvry2xTgi/LXLX6cqKryqtq5BtViTKeOa5vnCR8k3ISAEhEA2CHREuN1UNfhVG5vRcR7KyD/e1spjlRnjojYdd5psNNWB54hYSO1/r3mqapSvya8Cfr/y1dcqj7GYHXw3swuQSMMOvJvSJCFQGgQ++ugjxYG01Kc+9Sn1zjvvxO10A1toYry68sor4+6XjYNDoKgF4r72xohJRnmVV1VVVUX+eY2AT/yAcu7C2DvBwTpi/XfLVXOUk5Lp++ROFgwkQkC06etkCHLJhOhmr2UqHA4qYgrE4QBa4W4OpN3dgdqQVjpxn7vDPsam4Gv0KcK3ONy0hCbTZp9C2l/juIRfjWuKQJyQkuwQAkJggAR6WsJjI1GFao27iGldpEfVGdZMycZ464ji/+xTzbUVofdLxGJ0aOE3bAEGSyFfW4k7YBf/QyE9FAKOJnDXXXfpMes73/lO3Hb29fWpvffeW40aNUp9/PHHcevIxsEhUNQCcbe/Jo2Xaf+LNUEwjrb6sEYSL+aymlitZE+L4cdU6Ut8Rw2hLJEgGHOwcUxcob3/gEhBMSixx9tmnn8g7TY1uFSZKEJqn2qwAo1lRSA2zaHL0tMIGBxFIDafAvkuBIRANgn4jOjRZd5EY2P4ih1NpukvW/hELbiGa5bWt76OFlXnrYiI50FWTAp+F7vcFarO1x+3orTQSG+FgBBwGIFjjz1WcS7hhMLuzTffrOUSzk/ssJZLc0pHIHa5lcfjSfFXrsorGyIiNAcfkUg/4+BKtUcFohajewxtqasqjqbZet4MoYwSRFe2qoY+jWOSCsSGKbHlD51SIB5Au02BOFm7QpPDNAXinkB4USMswPaEBWyOnp1Weg2DY/h8IcryRQgIASEwcAJGrAK8L+rCaQgSn7uvJTI+RV3somvig0thT4/q4AjdLS1tHAyxg6N04zPqJVwKGKSPQkAIOJZAb2+veuutt+K277333lNDhgxRkydPjrtfNg4ugaIWiGEyHUoxxKmIklqsJbkPzWY6B9NUiyM0m69j0/Q4mXCoOPJoyLc5gUY6pjmGIOfi1B3x+2JoYrmd9a3B1qUSiAfSblMLn1gLYsNkOsHCQLsRtdsUYAMRgr+ZZMogx9Gmfeyr0djUrFrb++sYHBObeBvnkK9CQAgIgTQJmOOWGeAw1WnCLi+wWKqyn4Ug1YllvxAQAkJACAwqgbPOOktrh1977bVBbYdcPD6BohaIFQs/IcGTrHy7sSA6mmtUmculytxu5W2IXJU3fWSJylRtY32EP3FElGgzqFbCwFdKmZFHXclMq82mGoIcfKUC8STiCK1EOPBWKoE4IqhWuu1m/+ow4/A1zaYrM/BWmhpic4IYIRDr3MpBM3dzu3ndDl84HZTL8g03OJZVJTFrN08k34WAEBACaRBorAznqfckCPoX73SRqf5cqqEt3kAf70jZJgSEgBAQAk4lsGHDBi0Mn3766U5tYsm3q7gFYjZ+NgOVEOczjNEl9kWmDfKYqZLYhM1MkWRpFCPz7pYpXyiqJefGNaJeujnPbfR0pq/dZwiQnLPXbkhMQ5CDCZ67Otoku0/5QgG1WFA0olenFIg5y2Pm7Y4MBuOujvaVi2pXlEAcFqZ58hcVBjxycog+hyOAY1/QdB1CsTuO2XRknuJqyyHP5Mja+ZjnoeSHBAEgBISAEBACQkAICAEhkC0CPp9PTZgwQe3YsSNbp5TzZJlAkQvESkUEjIK5c1ml8gXY96irQ7U01yuPEZwDmtdwOqM+1WgFgsJxnNc3LK9FpWJic18r/kmXv9oQ1Djgh6da+Vs7VDdfz99YHTbh1m1JI1+iKcj1t9ldWada2rvYryqgairCGgmK8qtNLRArNZB290TkBOaAYxW1KtDeodtVG9Eu8K8xhFAzOBYE23IdHKWtrUU11lZFstKLAGGBmO+sqvfgGOuvTFU3+lVHV5dqb/GpKre1nT/NFFimtpqP9XirOS2TT3VEr1xk+YcmpxMCQkAICAEhIASEgBAobAIdrX5VX1utqiorVSX/IXtNdU2tamxuUVaGz8LuYWm2vugFYtzWloaw6WxYgDIEpn6hqtrQ1rb7wrmCcYzljxt6TCLMo0mZ+X39tR5DUIu9TrANsWmbQueO98USiCME+PjnrmhojTiDHYEYBwyk3QFbfeb2skBsLR7gml1pRAKPyRHd06IqU/KA2aHp6d1m5GoO86uPqIOWSRECQkAICAEhIASEgBAQAqyGaWuOVLaEFDLhuSQUUpU1omQpxOelJARi3JjuVp+qdLviCqplHq9qbjONZ1loMgSt8gQ5hVsjBO3yiKjTHYEG5THMp8OCuEtVVNertOUvSyDGD7CsQtVUx8nPWOZR9f6wHtt6IE2BuMZviqNWjfDnQNrd1lSnyg1uVp8r6pqVv66/ve5aQ0McvG57c/zjyirqVHt3a0jorfLF9o1FatUYjwVzKoN2Po7qt7u1IcIPHO20InKHScg3ISAEhIAQEAJCQAgIgVIn0NpopsUzBeBE3ytUiul2qSN1XP93Q4tYICiZsqNzK7W/3x3s75Bh9Pmx42nMiN1z1v/tnVto2/s9fP4hNGTYSBo/fgwNzeRyvetp3rCj6FG01F1LPasvpKE7OmlLx/vU0zeERn5+LI0bMyJr/ci83bto+9Z24nQY1NdHNHL/g2jc6KE22sXHdfJxzArHDdt3PB2YTn96t9OW9m3MApdiHvuMT3HdXbRj+w7aheq7D6PRI+y0EZWlCAEhIASEgBAQAkJACJQCgS1PXkMHue8wuuoib/29VH78ETR2NM+7e3dQ+5uv0Mp7b6TFy58P13N5qf3vi2hceIt8czCBkhOIHXwvkjfNFIjLaqhrzQIanfwI2SsEhIAQEAJCQAgIASEgBIRAJgS2r6M5e82kkJjrrqbWRy6niQn0T1vWLKWDjr8idCUOBkurL58e+r98cS4BEYide28iWxYlEHezQJzg9xh5nPxPCAgBISAEhIAQEAJCQAgIgbQIrFs6l2Ze0RA8xlXFGt/rU2p8N65YQFMuWN5/nTJq6lpDs0SDlRb3wagsAvFgUM/kmjvW09yRR5H+WYqGOBOCcowQEAJCQAgIASEgBISAEEhNoHcDuyq6gq6KXJvTpNKiWWNSH0db6ZZp4+mGQLBqRX0rLfnmRBvHSZXBJCAC8WDST+fa5g+TfYi72YdYNMTpAJS6QkAICAEhIASEgBAQAkIgNYHejSto2JQLghXZH7iD/YHtiMM4YDNriSdZWuLyOup55HySSDWpmQ9mDRGIB5N+mtfe0dlJOzji1JARY3MaCCzNZkl1ISAEhIAQEAJCQAgIASFQNAR2bFhGI12XBPvDlpnpuCr2bmZhelK/MJ3msUUDsMA6IgJxgd0waa4QEAJCQAgIASEgBISAEBACuSOwfd1S2mtmMECWu7qZg2PNsH8x06qTKqm173aamEmGGftXlJoDJCAC8QAByuFCQAgIASEgBISAEBACQkAIFA+Brc/cQuNPuSHYoUofqdvn2O+cGQiX3NTcvZpmiJ+jfX6DUFME4kGALpcUAkJACAgBISAEhIAQEAJCwJkEtq5hgfj4oEBc5m2iNYtm2W/o1mdozvhTgumayqqpY83ltv2P7V9EamaTgAjE2aQp5xICQkAICAEhIASEgBAQAkKgoAkMyIeY/Y+HGf7HXZwqVTIvOftxEIHY2fdHWicEhIAQEAJCQAgIASEgBIRAPgl0rqE5Y48PanmpnPzdj9B0m2bP65fOo6OueFS31sXm1n9Px9w6n32Ua4UIiEAcQiFfhIAQEAJCQAgIASEgBISAEBAC22nZnL3okueDJNzVfg6sNT01lh3rae7Io6ihv6a3uYsWzRD9cGpwg1tDBOLB5S9XFwJCQAgIASEgBISAEBACQsBhBEw/YiIX1QZeoAunJhNut9OKBbPpguWB/p5UUhtHmD5QIkw77M7GNkcE4lgmskUICAEhIASEgBAQAkJACAiBkiawgx6eO5LmW+peZuFtCNCPTp9K0TLuru0b6O75Llps1m3uYO3wmJImWCidF4G4UO6UtFMICAEhIASEgBAQAkJACAiB/BFgE+h5bAId9Ajuv2yZh2ouPYOOPmQ8UV8nBZ5dSfNvWB7RprQjU0ccLf/JNwERiPNNXK4nBISAEBACQkAICAEhIASEQEEQ2NW5jq4+YSbdY1lCp2i1p7qJqi+fRUNT1JPdziEgArFz7oW0RAgIASEgBISAEBACQkAICAHHEeiljWueoGVLvXQPm03HFhd5vIvpB+Vn0tRxIgrH8nH2FhGInX1/pHVCQAgIASEgBISAEBACQkAIOIRA745O2tbxPtHIfWj4zi7aOWQv2mfcaNEIO+T+ZNIMEYgzoSbHCAEhIASEgBAQAkJACAgBISAEhEDBExCBuOBvoXRACAgBISAEhIAQEAJCQAgIASEgBDIhIAJxJtTkGCEgBISAEBACQkAICAEhIASEgBAoeAIiEBf8LZQOCAEhIASEgBAQAkJACAgBISAEhEAmBEQgzoSaHCMEhIAQEAJCQAgIASEgBISAEBACBU9ABOKCv4XSASEgBISAEBACQkAICAEhIASEgBDIhIAIxJlQk2OEgBAQAkJACAgBISAEhIAQEAJCoOAJiEBc8LdQOiAEhIAQEAJCQAgIASEgBISAEBACmRAQgTgTanKMEBACQkAICAEhIASEgBAQAkJACBQ8gf8HW/StZNCAe6gAAAAASUVORK5CYII= />
The product labeled exo is likely to form in smaller quantities than the product endo product shown in E26.1. The endo product is favored due to secondary orbital overlap in the transition state of the reaction. Products A and B are not expected to form since they would arise if the maleic anhydride dienophile approached the face of the diene from which the isopropyl group is protruding as shown in the figure below.
Question 9In nature, thiamine pyrophosphate (vitamin B1) is a cofactor used by transketolase, as shown in Equation E25.4. Write the mechanism for this reaction using curved arrows to show the movement of the electrons.