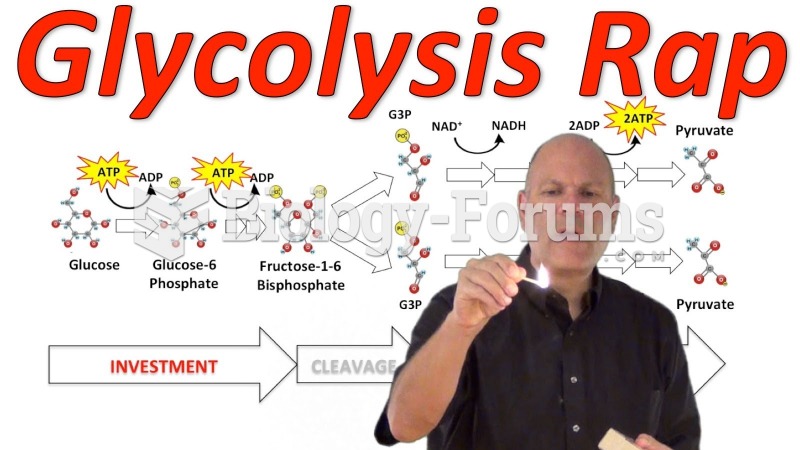
What type of process has occurred in the following glycolysis step?
 Question 2
Question 2xYKVKgcqB3bkAGBWqXKgcmB8HBBB4+j5Ezv/OH5nU2+VphcHrIkTmDHdbgbQZik7Qa01E/XTb9aemUXIb6ZN1SxCe4BWFpf7Ltb02sa8J7pVBwidm1t2PVVzy3uiLTXPyoHKgcqByoHpwQGRZgMbfgU51+jz9OibZi1MW9oYYJYAELOGzeYoARz9JcJmVk30zDKoqdycMio0ju1EAAAgAElEQVRAazZgf73GfEcToFUF2l97u7arcqByoHJgajiQvqW5JICfqZHoqeH/rpRi7blpTt+iEzUTtEE2FABu1g5O9adQZjRAw/xUpNbr0jP1T+VA5UDlQOVA5cBucCB9TB387wYTp+hVQMwxXaguLJkuPVHrUTlQOVA5UDlQOVA5UDkwwoEK0KooVA5UDlQOVA5UDlQOVA5MMw5UgDbNOqRWp3KgcqByoHKgcqByoHKgArQqA5UDlQOVA5UDlQOVA5UD04wDFaBNsw6p1akcqByoHKgcqByoHKgcqACtykDlQOVA5UDlQOVA5UDlwDTjQAVo06xDanUqByoHKgcqByoHKgcqBypAqzJQOVA5UDlQOVA5UDlQOTDNOFAB2jTrkFqdyoHKgcqByoHKgcqByoEK0KoMVA5UDlQOVA5UDlQOVA5MMw5UgDbNOqRWp3KgcqByoHKgcqByoHKgArQqA5UDlQOVA5UDlQOVA5UD04wDFaBNsw6p1akcqByoHKgcqByoHKgcqACtykDlQOVA5UDlQOVA5UDlwDTjQAVo06xDanUqByoHKgcqByoHKgcqB7orCyoHZhIH+vv7Y3BwsDS5q6srHJUqByoHKgcqByoHphsHZjRAGxoaCsfAwEDpF47b70r7Hweee+65ePTRR2PdunXb+3jWrFmxdOnSOP744+O4447b/xpdW1Q5UDmw1ziQ/iXP/Ez1L3utO/bJgmc0QNNjQJmoCqoKtE/K8JiVZhDXrl0bf/7zn+OKK66Il19+ORYuXBidnZ3R19cXixcvjs997nPx9a9/PQ499NAx86oPKwcqByoHxsOBBGIJzrxT/ct4OFfTNDkw4wFac8qrt7d3+/RXk0n1et/kAIP45JNPFnB25ZVXxl133RVHH310iZj19PTEAw88EHfffXe8/fbbpYHnnXdenHDCCdHR0bFvNrjWunKgcmDacAA441+2bt1a6mRAmMsrpk0la0WmNQdmNEDr7u6OQw45JE488cR45ZVX4thjjy3RlWndY7Vy4+YAg/jggw/Gb3/727j99ttL337hC1+IH//4xzF79uy4+OKL42c/+1l5BpwvX768gLcK0MbN4pqwcqByoA0H2BA25qCDDiqDPksrVq5cGYsWLWqTut6qHGjPgRkN0ObOnRtnnnlmLFiwIN56663inEVYKu0fHDCCff311+OZZ54pDRI1O+aYY+I973lP+Q2Yz5kzp0x1PvHEEzusT9s/OFBbUTlQObA3OGAJhfWt/MsBBxwQmzdvLtF7QYBKlQPj5cCMB2gf+chHwlFp/+MAI7lixYo466yzSiTt5JNPLr+zpXZwSlOpcqByoHJgMjkgggagVf8ymVydeXnNaIC2N7pbVKdOoU0N50XM3ve+98W//uu/xmuvvRYHHnhgAGnI2hBrz3KDyPz588uUxNTUrJZSOVA5UDmw5zgw3f3MdK/fnuuZieU84wGa6a/HH388Nm7cWKIpFpZbyJkgSnj6lFNOKWvVkrUWfZoSswDd9ZFHHhknnXRSAQCZpnkGAp599tlSzptvvhkHH3xwmWY7/PDDm8km5dpah4ceeqjsVtSG1ggRIGJqz6clRiPTvdq3evXqsDbLWj0K5WhHdkWaNrTGYmdkytG6sDVr1pSk+R2yVFjTzj55Ib/Wuu8s79bn3tc3jibp6zvuuCP+8pe/xIYNG0I/nH/++YUvu1tms5x6XTlQOTBzOcCPsKFPPfVUvPHGG8WnsHN8DLJGzbpX057NHeR8hPeef/752LZtW3kmDb/Rjkyfvvjii2Uph0GngShbzK5Ntj2zVpu/fOmll4qfZL/TN/hskV3xlpFYKpS2vVlnvhAv+EN5oCOOOKK8I+LYSvLmj/DjhRdeKP7IunHtG40frXnsy79nHECjHBaPo/Xr18fVV18dl112WfkUAwFDhAIBOIDXd77znfj85z8fwAOiENdff3385je/KcL2mc98Jv7lX/5lVICmPLsFf/7zn4fvcZ122mnxn/7TfyoKVDKcpD+Ax6233loWxa9ataooZypJtokhuOCCC8q6u6ZRaFYBX6655ppyyJMhwbfMQ1rXDjwyjfjVr341vva1rxWD08yreY1vd955Z+EbgISAP5R5AcR4PW/evKLk5eEk/tEOuzl/8YtfxHXXXReibDYO/OAHP4j3v//924H5li1bSj/rO210kA8A1zuVKgcqByoHmhxgw4Ayx6ZNmwpo+tvf/lZ8DLvP1rHHCdBsGOBfvvjFL5ZP/VgLjUT7//GPf8S1115b/MsnPvGJ+OY3v9kWkCgToGNXL7/88gLq2LFvfOMbBdhNJkDziaKbb745rrrqqrj33nsLWGITs91stsHwZz/72WJT263nZk8BLX73hhtuKO21e57/aAfQ8ErQ4e9//3v86U9/KmDt4x//ePE1FaA1pW8/udbZwAEED8n/9a9/LaBmtOYZxXDOlOvcc8/dvgvH+5QC2akjr9HIqMEIx05CowEK/KUvfWm05Lt0X/lAox2LKcjtMnrkkUe2R8UAk3ZKxLgYJQEy4yF5UiTKSjmNiFoJ0LvxxhvjoosuKsDo1VdfbU2y/beoJFDIcPnsxWQR0HXLLbcUcOazG/pVP3z729+Oj370o9vBIiPy2GOPFbkwctMuh1GbRb/teDZZdaz5VA5UDuybHGADRYXMYLCJZgnYUIPm0YgfYW9sVvrYxz5WNhTwF2Z2+AvgS1RKEGA0Yi+Vdc8995RIk3qcc845xc+M9s5E74ucAY2CGcCSmYd2pN0G4oAoX9A6q8L3aRP/cttttxVwx57mp45a85TeM3zit83A4McnP/nJ1qT75e8ZF0Hz0dJLL720ADOKAHhB4kYBSRw3pSFIhEM0KQHI2WefXa6bURTpd0bSZDTL9Xje2Vme+Rzou+mmm+KXv/xlGXUJiytryZIlJdqjbdoKJHkGpJi6dP/CCy8s07fN+jR5oQw8MtrL0VI+x5P/v727f7azqu4Avu5LbkIS0pIEyAstOiOCTTFQXnR0qkjoD1VG6IyoYMRCdap/kcP4g5VRrOBUrEqjTqf2h7ba1sYgQQww+BJUIIA35OXmvp3O5zlZNztPzrm5yb25mHv2mnnOc87z7L2ftdez91rfvfba+3g2WXm+Z7gH9PCEZX0BPkrqK1/5SjP6wofn4Q8Qk0dHdB2IotSUqXwjQYBvsSNB5QLUZOR94u2uu+5qPJkCedUxyXONFikQe6VRnkaH2oMYtgrQUlL1XCVQJZASoP8M6L7xjW80g1D6jO4o7Qu9R9fRw+5zGHAS0IHu0UXu56BQ2aVuzme1z9Kkvl1I+nb+fr/xRRcaXLObBv/4po/ZBPXDL33NVgKLdD1Z0KN33nnnGVOt+JMfv8pfiG6Xho7OvP34XWnXT1mllVazPvXRuJ5//vlm3zNJjFrsJM8LptNoMBpCupmNGowIuGOBCcBG/JbpTp0oY7TO1inczw6k/IU0yj5VOO0ygKSDAz86kTogbvFdu3Y1ygGPAIpp1vSucVEDmeoLUF199dVz5eK1rM/OnTub0RBgoiwdD//KNMqzSz8ZAVbqpsOaphQDoaNyiz/88MPNyIv80S233BJc21ziOjW+gSHTjrxr+/btm5tKNCW7GE8anoEt3kXgDO/KfPDBBxs+8FyS95SrP8kllaX6A56VqgSqBKoE2hKgF+lj05lmTNCOHTuamRd6jh5CzjxSdKfBsu+8UgaB9KDQE6EUwA86m72gq+m0tC/0+lLZF7yxffaMpMfpb7aP/jabQD/iOXW2NGynwTB+8MGTVm4vkrYw+c10TWV7fKQ9ko4sziaPHkVctJdOt0wXbTXOzrhGZCQgNosnJOmmm25qNi5NoACwaOBGNoIR5du7d2/T6Lh3ATkuVmCtBGjZ2LLc8uxe2Qg1sBIAlWkX+p0y0BESeJjT1/F1ajFuH/vYx+Luu++Obdu2NSCJF0u8g3ymQrmKdSa/8QawqFt27pI/AfumAQE1IyWgSx5lCugns+yYPGkbN25sVk9aPGBBgGlNcQs6N5lZWSmmQswa0KM8YI8LG7jbs2fPXCf3PLyIUVCXVFoLkRO+uOKBvUcffbTxLqofr6EYQHLqRd6POlM+eEtZyHsuz+9Vdr1WJVAlsLIkQM/QXwb++/fvn5v+Yyduvvnm+MQnPtF43ukyadkUU6FsDn1napJtEq8mz+23396AtdTF8wESugkIcqSeKm3N+UqaLcEj+yK2zYIq+l6cnBgwtsXCKlOY6oV/+pt+l1bIDZtAf6qjcBrAE29p/xJEzsevNNJLU9Y1855v/S6WfAMD0CB83hMjgVxByEULlDhQaXyBATFQSRqqRqsjAjUlZSMqr5XfywZWXl/Md3xwJfNMAUV4QxTC7t27mw6hDsjzdXwjHgpCJwKYeL1yMYF0AFOCtOzsrhsxpeeI0nAg5YjL81t6cV34MIp08Ih9+ctfnnOLyyOAlcIyvZhThfgD5rj3yVZ5pgkAaTENAJ5Ojr92TEPDSJ8PigM4szjDCBUo5XJXjpW5yPPwnO8wFYG6OSpVCVQJVAnMJwEghMfMbMu3vvWtuY2xraZ0WKmJSr2ZfylH/9DJwA2dbjbBNfq0ffTjgc6aD+T0y9fvOn4MbHnBOCXMzABn7MCtt97a6E8zJBlrrF6+O2d9zOoAaWZtXMefPGyS32lfyjr24odezvpJi7dBooEBaIy9BgdoecnQPMDCK9SPTNEBaTqOTgZICCYH7Bh1HRNpRPMZc/fkzUa5FI3MKOxnP/tZ437WmQCcG264ofGc4RnvbbJKxugM4Z17XUwemfCEmXIE0HSI5FVa4Cjr2i4TcFOmjsjzRcHogDmq4h73DO574Aw44q2zFLtN6iC4FclPMVjxo2xTjsDguQA0ykJwKY9hTjmolzgRYI1HT73UL71+pq/Lurd5rL+rBKoEqgRKCdAzZjPMFggdMfCl32yQTefR/W2iY+hcniX2wxQgHcmrz0tFj6bOpY/nsy9mc5bSvtCHdKNtpHj3rOrPTXcNrNmJBGdlvcw40dFI/XjQ6H5lGIyzneyS+pSEd3XoRWlby/r1SrdSr53ZclZoTTU6jT7BkWm2++67LwT992scRAHImRLT2TQ6QEEHBJCUiZRrStRZZ82OJb3GCBwCBOX1pRAzEIMPpOF/5CMfaQDQfMuPdX6diByMinQg9Sjrc668GSmRScpDfuXjj0wQnnRuU6/p2ev1HF5M8XMICAbQUMq2+bHAD/I36jOK5TUFrO1JZLoTAd54lg7wk5bS9LtSlUCVQJXAQiRA19Ej9BX9D0wAZmJ72Rd6pxcBH4Ac+0Iny0cHsRV0E/2pbN8BQEH4bBVdS0dJ75mmF+WRHi2F/lIf5akPSjBp8D+f/jbAZyvlwydPGv7xWdqH5FE6YJD9zEE7W0Q2bKe84uDMyLCfrg8SDQxA0yBK5A4wAGlWEs5H8ogVcCRpMDpOlmcrDvP04g80wmzUnqlBaai8dxobWqrRgLKzwZrCFJBqFHM2ojB4DoHPJHXJTpPX8uw6nnuRuAvxb1z0OiGSPo/kDzAU19Vr5NUuV1oKDuiUn0zPR2byeKYpVXETlBu+UvGUCgPw1hbcr1QlUCVQJXAuEqA36Co6hy4FVHjje+3tVZYrPd3jSGIv2BA2xmHLDVOntqYwOwHAeJ7nAC0GyMJJgDT3lblYyvp4hnqZYTCIPZv+lo8Nshk6IGfAjce2fUm7wGbYluSxxx5rZkrw7Zr7Dt/ZW55JDgWeRGUNCi3+TV4kksoGV7Kr8Z8v6QQMPtBlGo0nSufoRYCATpUARl78tEkHM1JSpg4qjTIBFlOJVvaU5H5ZzrnUp5223YHK5+BJLBi+1SN502EEhNq6QqwXXnRgignYMbIrqQRE5fVe35O/rB/+yo7ZlpXOXMrKdAF+LYzAE74RZZHKr3yudwnk5vPKe/V7lUCVQJVAPwnQGQ46qNQf56LvsuzUe6mP/QbMOAHmsy9pM1LvlXxk2WZy6HJ6G2/SADxCS+jrtC+uO7I+vuMj9abf8xEdW9Zd+qxP5ktdziZahGffybyWaZw9V1lAq7PZkF7pyjwr6fvAADQvrWxY2RHO92UqSwNG2YAWWlbJR+bh5hVk6tCJshE6Axg2KuQ6Xipq1z/rovyyQ0lnhPOFL3yhmabMzieNaUfAzUID6XglBYJa4cNdzaOoUye1n5nXe53backhefRccWWlrNwDyMhKjITtU5ApA0elKoEqgSqB5ZIA/dXWYQt5dq98rgEoCyF6MO1LnuUzhWhbD3Fh4nHTvhj8iw+jLy3SAthSz7afhw+2LvO27+dvaUrCR8mLe+VvNoL9WwiV9VtI+os9zcAAtGxc+cK86H4NMdPMd9aogBWkkXPnGoVonJ6FsmGaUhNoyaMknzTls3UeKzLFRgmqNwVpiwf5jJykNfoxOuI69jxgBOWz8nnNxQV8lM+XvARSfpf3xW055iMufcBIHFzGIKS3KvOdrWNnOmfPLzux78oDXk0Xp6yM/nI7DIqHXDJWgyfP/UpVAlUCVQIXUgL0cB6eQ3+di75L3lLvlWXRYaYNefjdT11NJ0rHC2WXArqxHEArU1rxt+yLUBS6EwlvcU9slyB+04h0p9Xt7Avekwdnz3JtIXXi6ZMu9Td751nKSUoQpz6mgdkPz0XulXl5B9lINjDrl+Ws9PPAALR88flCgZ+Fjkoyr0bj0IAcOWVpBY7gd3uqaYgaEZJWo9cJbBBrybJGJk3Z0HWez3/+8808u3J5y3iiAA27N9sI1rYTGvgDDzzQrNY0t5+N2LOUqSEvlNSdDJI8t+xAZdmZpt9ZB7PZ7/33399sYCgdfhzKzd88Xwsl/OW0pDw6smsUzEMPPdSsQMUjUGgjRDK2zYe9hMjZO/D/mt5JpSqBKoEqgQslgdSbeabz6NZz0XfJG5uinNSbdJw4WtsD0WU8XFku2+I5Bv88Y+wEoEX3sS/KkZbnzCbdVusDQTnD4B596b4YN88CruwG4DlJeFEm3tq2K9OU57RF9Le8WR/ntCvSIKEltoayp5p/aUGeI5064NFCMdsk5UbsmbdJvMI/BgagZSPJ95nbL5j+4uItAVOmcdbITOFZcgwkCMQHjrIDSGN0Y3sIgei9SBk6jhEM0miVlWS7DJ0L8Qb5n7Hcg41XSCfiSTOlp3PpQDqSOmVj1UnthybYFI9lB8vn5FndlVl6xXRA5SWlgvDbtCElYf6fQshOl2mNxgA0nrN8ro6FN+UiMWOAKFlboDDftKMRnw5JLlk/ZQCgYhXEvQFr9hKyxYfVoZ7DQ2nq007eZEWOFaDlW6rnKoEqgQslATrRQT866FiDSYNX+hMQ6UX0GD1HZ9GdbAk97Dsbw07Q6fnPML3KYCMM5gEwm8vSmfIpB9jJ/73kZTPTw1bRmfSpBQb+AYZ9A9RsPWXxHPCX9fFMz+Bps1iOfemnv9U9y3IW76buaQeSf2UjdsziA7qaXWuTdOTj+fgkr8zbTrsSfw8MQNPguVG5iXmx7FljE1XThrbb6NXgNHBxVI888kjzF0TKuPfee5vGBKRpxMCXzqCh9SP5pM3Rg3QlGBKcKX4LiNMBypU/7mU+HUoHQK6ZUtWhrfIBanjbdE6rFm+88cae7BiNGC0J7Bc/hjzPPm/4RDqAcpJHgMrO+9zfgFfy0CQ+GedFtpnfdfxxzbsOPHJRP/74401H5dnKGLEsI88WW/i7py996UsNMHYdb8rxjhxkRQFSfCkr8vUuE/iSVQnusvx6rhKoEqgSWEoJ0DnsgZWOdDJ9x76wCcAJMJSb1ZbPBV4M/nn87UlJX5oNoLvpsrQpyu/nQFAe3edI3eda6m56mNeM/gRu6MxccCY9+5Jl0+0AHfJstlKdgCM2hoMh7YK/emoTEGbQbz9MdbJwjC2hrw3uyQJfyZv8+Juvfu6pW/LYfuZK/z0wAE2j9N+URhG8M8CQEYGGVzaYfOGuQex2sdcwpUNGBTbcKzuERpgNO/OXZyCuHEEouwQPOuRnP/vZJoaAp4oXLSk7RP7O0YOGbVNDAfn+IcEoCY/+IUBjlo/ruCSgxv1ySTPFQSnwzOmQCK/5HL+BQGX12vy2LL/8DqzZKoNywquFBsDhE0880ciODOxKTY5JFAFZ+7cHo0E8UHi8ZHgkF+UCi96fkRyPHJJWnT0LUTClwmou1o8qgSqBKoEllgB9S0eyC7z4ZjLoMiANkCl1aT7aANLWEQbV9Lftiug6+42Z6qO/EpTIX9qPLCPPBsxtnZ32BSgyi+C+Dc3NOngGko8eTv7yO71pIGxgTvdKZ+bCVh7KTdtHvyeIlBc4o9/Vie2UlsfOHm8Otsa1dl16Xcu6uef5zoNIp6zjCq89TwuABixpbAy8lw40QPqMv06DNECeHECGl82ICAED4s2MOuTNhq3BtRtdk+Hkh7TuZ/p2hwO0dBwNUdk6qvTA4IEDB5rvOowtI9xL0vF0QB3KaIwXTR4AJzubEZM6u2/6z5+q6zwIINNxeNzIJj1gni1/UvKfvxdyVpYObmSJP6M3ANEu/kZXyZ9AfnI3ejMFij/xFO4bUZo2veeeexqApiyjMQomlYt8FCHgTcl5lnpRHkZtlaoEqgSqBC6kBNgLAE2IC13GpgBopg9NOeb+mPQwveYsDWAGzEiD2AD6mq5PUMJWlLamXQ/lue/wHeU1g1X2AUhkO5TFM0ev4tMMikE9fc+usG3sJGCoThwHvjuyXuqiXHmsvLRozT3AlP62H6g9MfFgahbA8z/K7Azbpu6pu6VJXtM2tuuX9c/6ZR7nQaCBAWgMN1evKcT0FHnBGpNGo2FqOEha06A8bAnOAAkLAQTv88YBBvKh+TqQ+xpZNiy/NW55kjRcR0nl1Cp+zNEDUjpEEhAkXkBZOo3OAaQAQQLmnbmoPQ+/wJ49Z5AO6W9Gyk1cs9zkN3+TS8omr53tjB/8GQ1a2Zn8qReFRDkBwVzvyuaBpCz8rRNZkQevGf6AtJQPBeNApk1N1wJ03helB8RRBqateSMrVQlUCVQJXGgJADE8RLma3/PoXHFd4sPco4fpNmfeLB6pBGcAFH1MzwNoBrR0ovQLsS+lzi7tC71b6syUgxkN9sKgnX1JIEVf+43YCM4DhAehJ2yIvHjzHTD1nf5le4A+PItLpr8Nrs2UAIUIn3lI5/t89cs0Wb9M7/og0MAAtHyZGooRBVCgA0H++dc/mSbPwIPARXm4rz/60Y82gEjnMmrQEZCyztZgNCwNGTn73Ys0VkGRplZ57zR8AaIAhw6cS5EzLxez+lAQ+NDpLCjQeRy9iGeJIvj4xz/erBhNz1mZNuvmGn7L32W6s33HF0+aEZm6AbWAGG+aoxcBy/4iBSC2uifBWTutsrwLo1VK0EpOzwNKgWiKrlKVQJVAlcBySYDu4nmit+kmZzq5bR+AIHqKbhQ6AghZGGbAbWDNOwWkIXq9n71wP0FM2pf50tOZ4t7sCmBwy8snHphtM4vSnnVgb8zU4BfYUzb+5rMvvIAJ+AyuE5zlO1AX9iTtoO9t+WTarB/bkXYID34PAg0cQNMZABMxV6bFBK5ncH35wgEfq124Z7lqdbz0XmlM7gM2Go0RCgDSjzRs6TV2IEKD9bsXmX59+OGHG4BmdKXTfPrTn24AVRuclfnFY/E24cnUbD/ww3toZGNLDKCzFzjTGbnGkwAddVgMcd8DXOptClY9exFZkvunPvWpZkVRG5yRfR7SUgTK9i7tISf+Q4yhesprqrNSlUCVQJXAhZYA3WZFIrAD9Bgo81CJq02wlTzQTzz9ts9gV9gXszv0btoXeldoCj02n30xKPXstEPS97IvbJVwECEmwBmdiU/2kB5tg7PkVXlAJ1DENqhPv8E/DyKbxXPGvrTBGTuiLmY6lIvUUx36kXvkon6cKlnPfulX0vX+qGIl1bKoi46RblteMC9eIxKTlmBFQ+Q9s3WEKU2NqSQNhmdNwzYCEXsgfT/SIIEIAf3ixIApnbEkowquY968R7761Xj10KGm0zz44N81fLQbepnXd/UQyK9zex5XMz51KOS6zsHVbp81IKifh4lrW8fVGeT3ndwWQxRGgiVlGsWhVDzJn2dTXBRG+0+Gjf4OHHi2qduRI280wPmdO3c2/AG+Rp3AmQUT3/ve95v3ks9cDO81b5VAlUCVwNkkQN/y3Dt4woTHiJmlc4G11HV0tSlA3iV6rtSt7EACIuDMzABbI30/kl44Bw+cGSHhOO2to46L1X3yyXj8m99sAvl59tit3bt3x+27dsWmjRv7Fd9c9wz2RR3wC+jxfNHrdDe+2ZPcEkTZdHmb5Gcr2ZS0t6ZAeRN7EZmmV5K9puPJAxAcBBo4gFa+VA3KVJoRTIKRvK8TXXnFFWeAM/c11ttue3+z7cT01FT88cmdkDNv+6wh3nLLzc1ChBMTE7G+2X7i8rlkGjdQwfNlavO1V7vg7DOf+UzccceuWL9+4bvhA38aO8ACkJ3yfJmz78aF6SD9wBmmKBQjO51I/q7S6d2B5iqxwC9kbZuND3/4w02ONn86vJFcG5xJ7B398If/GV/84j/EiwcPxvve/76m827burVJb2SVdOzY0cYdn7/ruUqgSqBKYDklQI8abIov40FLXQd0GPRv3rzpNHCGN4NX+o99Mf0JBG3YcGls2ripJ+vKBJiEuVg8xb6sXbeu0dmjJ71SBrPPPPPzxvP13T17Gttgv7P77rs37rjjr84Im+n5oJN2jycNCOOYAMy6DgAAresYWHvJJbFx05n1yjIBtKu2b2/CdfCAALn+AG24AXQfuO22BphxnpDHxj7yyOeslHNvgNY5uQv+8OKmtS4GIeWI51x4BSK2bt3WHAvJ1+10l8fmzadAWeabnZ6MJ/fti8ce+3p889vfiZd/+5vY9YHb4nOf+/v44Ic+FDHU3/WbZZRnIMVqnLSNTtUAAAZjSURBVMUQ5SGOwLHUBPj6n87zoc7sTPzuxYPxPz/6r5iejfjpvp/E+OuvzhU11JkJBxodGYrRAWi/c5WvX6oEqgT+4CTA++M4F6J/t2zZ2hwLycceAYOONh09cjie/MlP4jvf/nY8see7MW7G5923xv33725mZoZHT/1jQDtvr9/sS25t1Ov+2a6xhQCkY2E01IDZLVu3hmOlERM1MjwUw5wpPSp3GkCbnu3E1OxQxOjqBheMjp7a7b5H3nppCSTQmZmMvT/+7/j6o1+NZ1/4dWy7clPcdMP1sX3L5XHwl90l0JMWIczMxLp162PzFVfGmnUbluDJF18Ra9esirdefVXc+M4d8eT+Z+LE8SNx4Jmn48+uuybGxw/HC88/FyNDnbhsw/q4cef1sXXLmQrr4qt15bhKoEqgSuD8JHDsjfF4at/e+P6e78RT+56Oa655a7z9bW+NTZf9Ufz2xV/F1ORkTE1PB3hgZuiyjZtizfrFhbOcH6eDmavrSIgmHGlyJmJ65vTVqXMAjbtycroTMXpJxOjaiJGZmO1UgHahm83U9Gy89vvx+O3vXgqv5sjRY/F/e/fF4SNHY3ra/2seixkrPjsR1117bXzwzjvjz9/Z+18CLjSvb3b5Y2suiXe9+z3xyd+Pxz89/s/x9P6fxj9+7Wvx1P6n4/jE8Xjqp/tj9Zq1cdvt74l7770vrnvHqS1J3mze6/OrBKoEqgSWVwKdODE5FeOHD8ehQ6+GPQdeeeVQ/O+P98Zrr4838WRi3DqdbtzbNW+7Jt5vavUvbHBebf9yvKtu/F4nZodGI0bGYtLUUOFKmwNoI8PD8fYta+K9bzkS02MTccXqmXj6xZGYsd/I7EwDEgZk65EL/l7EDVgUOTIyHK+/fiyeO3FlDL/lLyNePhjjY+vjX39+LP7t2aea+ANz7l6iPDteuSRmth2K19YeC4tGJydP/4PzC874m/iA4eGh0P46w2+JS3f8dWw4MBG//+VM/MeBN+JHB/c3nM3Mro7tV90am3beGfEn74n94xvixMtHuvlq430T3159dJVAlcBySYCtMPt1YnI6XnppOp6b3BJTW98VMXEgDo1eEj94diL+/blnGmBmZSeyCO26l1bH65e+Ei+vORwb1o/F8YnBsS/L9W7yOezZyFDEGycifv7SREwcj7jhquF4+1VrG2yQ6YY6rL8N5Dqd+PVrU/GrV09EZ3g0XnxtIv5l/+F4ZXJ1dKYnw1Rc4+LJnPV8/hI4Od+sI52YnGz28frFC7+IyYmj3ZHL1HTE9JRd/Sy/7D6nE7Hm8svjmmuvjW3bt4XFmTPcoXn//Lm5KHJ2Qe1QrBpbfXIvtefj+Wefi87h8a4MIN6x1bFu8+a5HbmHYjYmJk50m+2AyOmieJmVySqBKoELJwH/bzk01DhVJuzy/9LL8ZuDB+PoG3Rls+tsBBvTme3aGC6bsVWxdtOmJr5s2/btMTY2EtNm1KrevCDvqWvPIqaGVsf4sanYccWq+Jud6+KG7WvjTy9fPQfS5gBam4sfv3A0/vaLv4injmyJmD4eMT3RTlJ/L0oCJ4FX15XGnRYxNNztNNMz3Y5TuDrnwHGT7WTeRT3/YsvcrFyJGB5pjqERHrVOxMx0xAy3cOOS7MqxUUKUDzlaNFAK8mKrd+W3SqBKoErgXCVACQ6drhf9Bsps8urcJvp0EE1LWw7L+Xv1+sZG3fOOiXjo/qvjsrVzk5oNF6f/Khjzni5bMxKrDr3eBWcz3b81KpLUr0shAdjBfOXYWLczKXOoEzHc6inSASL+vWBAdlHuK15gdtVoV240SsqqMxQx1enKqBkhtmTYt8B6o0qgSqBKYAVKwMCVfaEvT+6J2diXXkjMYJZzYNDty3I2g47IwJm4dPW6ZmeC9qP7ArQrNqyKT753U9z+xkjE7HT3aOeuvxcvAR3IWlueoTlHz9yX08tvRj/plj791kD9amQ2bH3ymd6xKqOBagq1slUCVQLzSCB1JRvje0N5buWrurMlkGX4OWKbk05cv200xgSltajvFKeYNGC6+iBaElu2n2e+rPo2egm/lFNtrb0kVK9VCVQJVAmcLoFSb+adqj9TEst9hp/t2zmHoU8y0BegLTeD9XlVAlUCVQJVAlUCVQJVAlUCXQnUzU5qS6gSqBKoEqgSqBKoEqgS+AOTwP8DAdR7hBAi73AAAAAASUVORK5CYII= />
1.tautomerization
2.oxidation
3.reduction
4.isomerization
5.none of these"
Question 3How many net moles of ATP are consumed or produced per mole of glucose entering glycolysis?
1.two consumed
2.one consumed
3.zero
4.one produced
5.two produced
 A beam-type torque wrench that displays the torque reading on the face of the dial. The beam display ...
A beam-type torque wrench that displays the torque reading on the face of the dial. The beam display ...
 A typical two-step ECT circuit showing that when the coolant temperature is low, the PCM applies a ...
A typical two-step ECT circuit showing that when the coolant temperature is low, the PCM applies a ...