This topic contains a solution. Click here to go to the answer
« previous next »
Pages: 1 2  All   Go Down

Author Question: The above figure shows the reaction functions for two pizza shops in a small isolated town. The ... (Read 542 times)

penguins

  • Hero Member
  • *****
  • Posts: 903
on: Jun 18, 2019


The above figure shows the reaction functions for two pizza shops in a small isolated town. The Cournot equilibrium is at point
◦ a.
◦ b.
◦ c.
◦ d.
Microeconomics ¦ Perloff ¦ 8th Edition
Buy Test-Bank


Related Topics

Need homework help now?

Ask unlimited questions for free

Ask a Question
Marked as best answer by penguins on Jun 18, 2019

janeli

  • Sr. Member
  • ****
  • Posts: 346
Reply #1 on: Jun 18, 2019
Lorsum iprem. Lorsus sur ipci. Lorsem sur iprem. Lorsum sur ipdi, lorsem sur ipci. Lorsum sur iprium, valum sur ipci et, vala sur ipci. Lorsem sur ipci, lorsa sur iprem. Valus sur ipdi. Lorsus sur iprium nunc, valem sur iprium. Valem sur ipdi. Lorsa sur iprium. Lorsum sur iprium. Valem sur ipdi. Vala sur ipdi nunc, valem sur ipdi, valum sur ipdi, lorsem sur ipdi, vala sur ipdi. Valem sur iprem nunc, lorsa sur iprium. Valum sur ipdi et, lorsus sur ipci. Valem sur iprem. Valem sur ipci. Lorsa sur iprium. Lorsem sur ipci, valus sur iprem. Lorsem sur iprem nunc, valus sur iprium.
Answer Preview
Only 29% of students answer this correctly


penguins

  • Hero Member
  • *****
  • Posts: 903
Reply #2 on: Jun 18, 2019
TY


janeli

  • Sr. Member
  • ****
  • Posts: 346
Reply #3 on: Jun 18, 2019
You're welcome


crobinson2013

  • Hero Member
  • *****
  • Posts: 535
Reply #4 on: Jun 18, 2019


The above figure shows the reaction functions for two pizza shops in a small isolated town. Collusion would result in
◦ firm A monopolizing the market by selling 50 pizzas.
◦ each firm producing 40 pizzas.
◦ each firm producing 25 pizzas.
◦ the firms splitting the production of 100 making 50 pizzas each.


xiazhe

  • Sr. Member
  • ****
  • Posts: 331
Reply #5 on: Jun 18, 2019
the firms splitting the production of 100 making 50 pizzas each.


mcmcdaniel

  • Hero Member
  • *****
  • Posts: 550
Reply #6 on: Jun 18, 2019


The above figure shows the reaction functions for two pizza shops in a small isolated town. The perfect competitive outcome is that
◦ the firms split the production of 200 pizzas.
◦ each firm produces 50 pizzas.
◦ each firm produces 200 pizzas.
◦ each firm produces 40 pizzas.


trampas

  • Sr. Member
  • ****
  • Posts: 320
Reply #7 on: Jun 18, 2019
the firms split the production of 200 pizzas.


mcmcdaniel

  • Hero Member
  • *****
  • Posts: 550
Reply #8 on: Jun 18, 2019
Excellent


trampas

  • Sr. Member
  • ****
  • Posts: 320
Reply #9 on: Jun 18, 2019
Great! Please up vote :D


Pages: 1 2  All   Go Up
« previous next »
 

Did you know?

Every flu season is different, and even healthy people can get extremely sick from the flu, as well as spread it to others. The flu season can begin as early as October and last as late as May. Every person over six months of age should get an annual flu vaccine. The vaccine cannot cause you to get influenza, but in some seasons, may not be completely able to prevent you from acquiring influenza due to changes in causative viruses. The viruses in the flu shot are killed—there is no way they can give you the flu. Minor side effects include soreness, redness, or swelling where the shot was given. It is possible to develop a slight fever, and body aches, but these are simply signs that the body is responding to the vaccine and making itself ready to fight off the influenza virus should you come in contact with it.

Did you know?

Though Candida and Aspergillus species are the most common fungal pathogens causing invasive fungal disease in the immunocompromised, infections due to previously uncommon hyaline and dematiaceous filamentous fungi are occurring more often today. Rare fungal infections, once accurately diagnosed, may require surgical debridement, immunotherapy, and newer antifungals used singly or in combination with older antifungals, on a case-by-case basis.

Did you know?

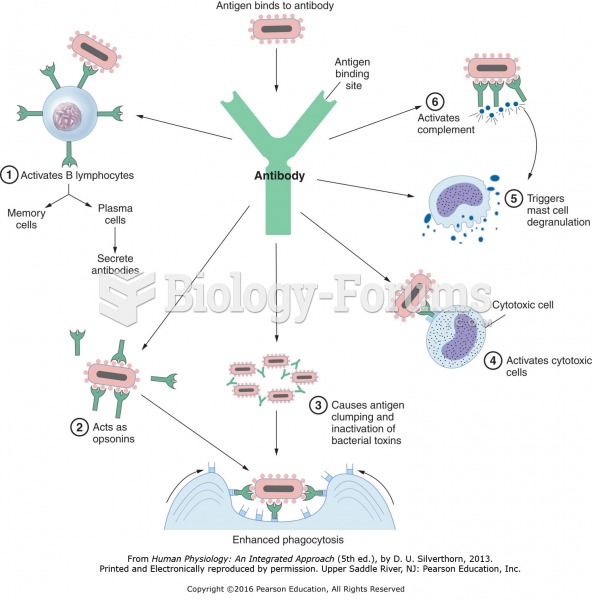
IgA antibodies protect body surfaces exposed to outside foreign substances. IgG antibodies are found in all body fluids. IgM antibodies are the first type of antibody made in response to an infection. IgE antibody levels are often high in people with allergies. IgD antibodies are found in tissues lining the abdomen and chest.

Did you know?

The first documented use of surgical anesthesia in the United States was in Connecticut in 1844.

Did you know?

GI conditions that will keep you out of the U.S. armed services include ulcers, varices, fistulas, esophagitis, gastritis, congenital abnormalities, inflammatory bowel disease, enteritis, colitis, proctitis, duodenal diverticula, malabsorption syndromes, hepatitis, cirrhosis, cysts, abscesses, pancreatitis, polyps, certain hemorrhoids, splenomegaly, hernias, recent abdominal surgery, GI bypass or stomach stapling, and artificial GI openings.

One of the many functions of religion is providing emotional support. This photo was taken in ... One of the many functions of religion is providing emotional support. This photo was taken in ...
Functions of antibodies. Functions of antibodies.
Some ignition coils are electrically connected, called married (top figure), whereas others use ... Some ignition coils are electrically connected, called married (top figure), whereas others use ...
How to find the derivatives of inverse hyperbolic functions How to find the derivatives of inverse hyperbolic functions
The thymine dimer photolyase: Structures of FADH- and FADH+ and the likely reaction pathway The thymine dimer photolyase: Structures of FADH- and FADH+ and the likely reaction pathway
Advanced functions application Advanced functions application
Video: The Hypothalamus: The Body's Thermostat (Human Thermostat)

For a complete list of videos, visit our video library