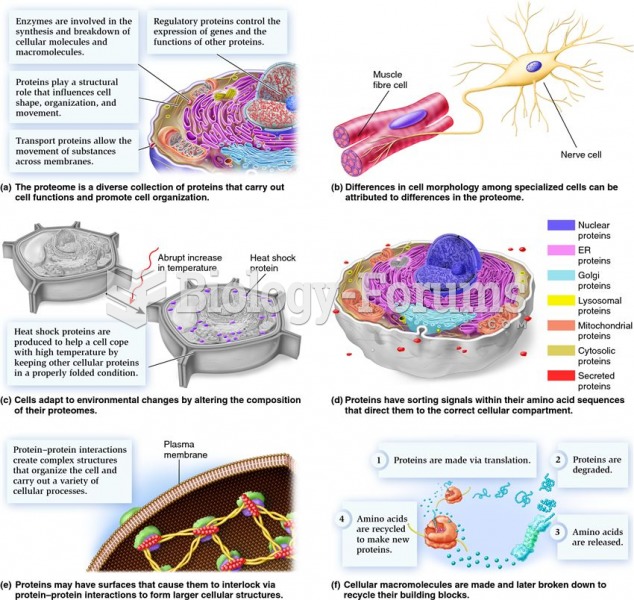
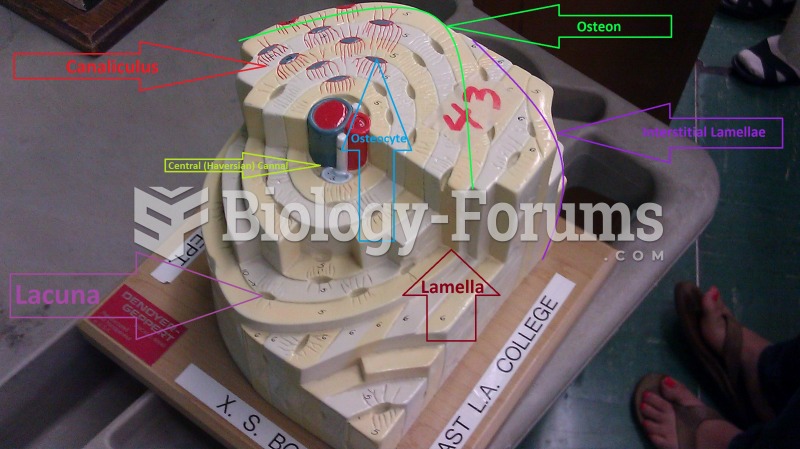
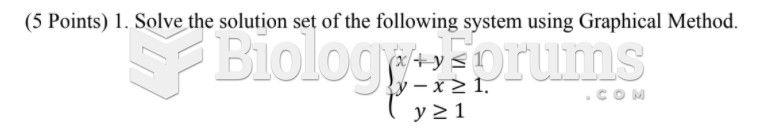|
|
|
People who have myopia, or nearsightedness, are not able to see objects at a distance but only up close. It occurs when the cornea is either curved too steeply, the eye is too long, or both. This condition is progressive and worsens with time. More than 100 million people in the United States are nearsighted, but only 20% of those are born with the condition. Diet, eye exercise, drug therapy, and corrective lenses can all help manage nearsightedness.
Of the estimated 2 million heroin users in the United States, 600,000–800,000 are considered hardcore addicts. Heroin addiction is considered to be one of the hardest addictions to recover from.
Sildenafil (Viagra®) has two actions that may be of consequence in patients with heart disease. It can lower the blood pressure, and it can interact with nitrates. It should never be used in patients who are taking nitrates.
According to research, pregnant women tend to eat more if carrying a baby boy. Male fetuses may secrete a chemical that stimulates their mothers to step up her energy intake.
Giardia is one of the most common intestinal parasites worldwide, and infects up to 20% of the world population, mostly in poorer countries with inadequate sanitation. Infections are most common in children, though chronic Giardia is more common in adults.