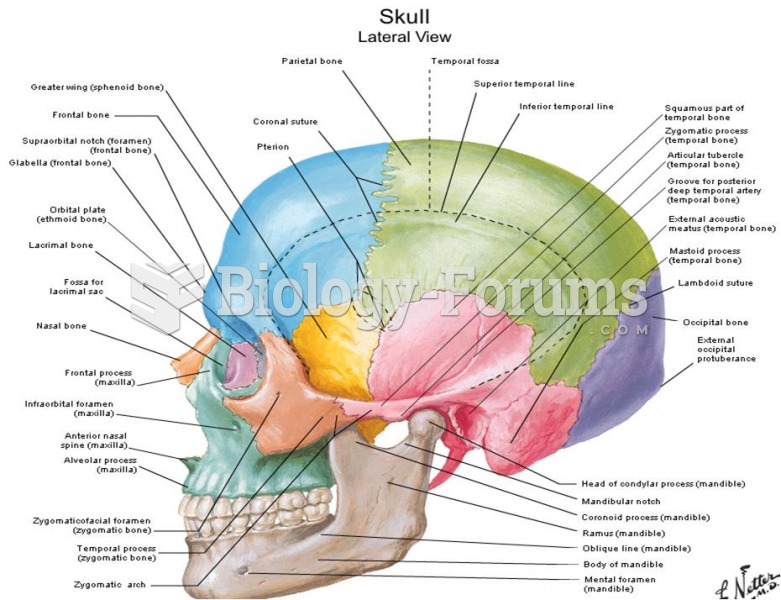
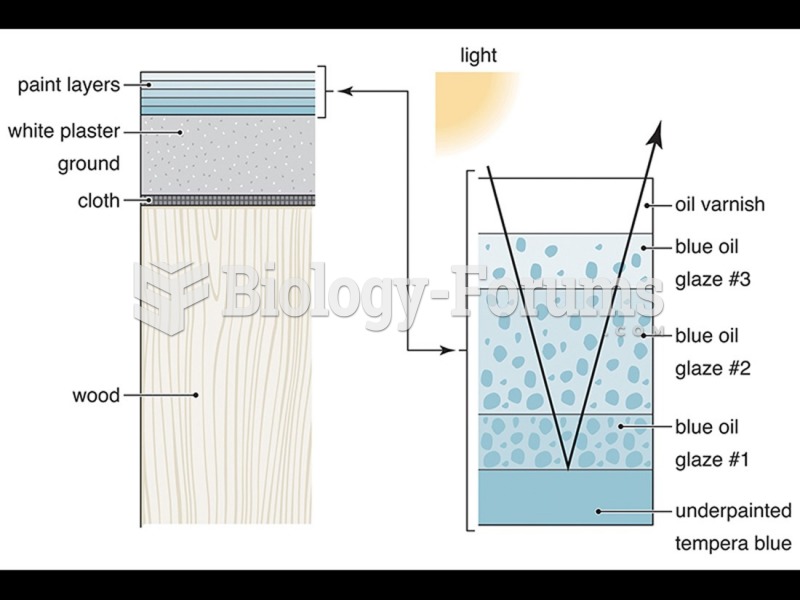
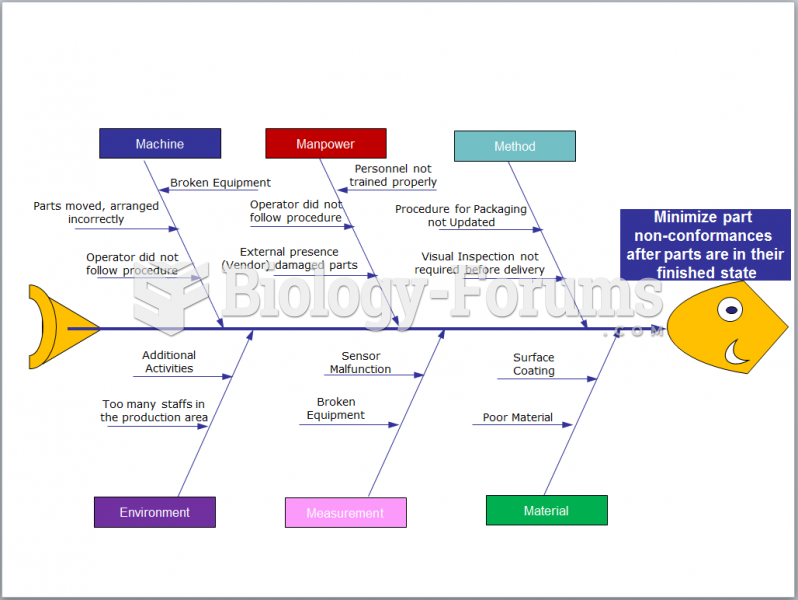
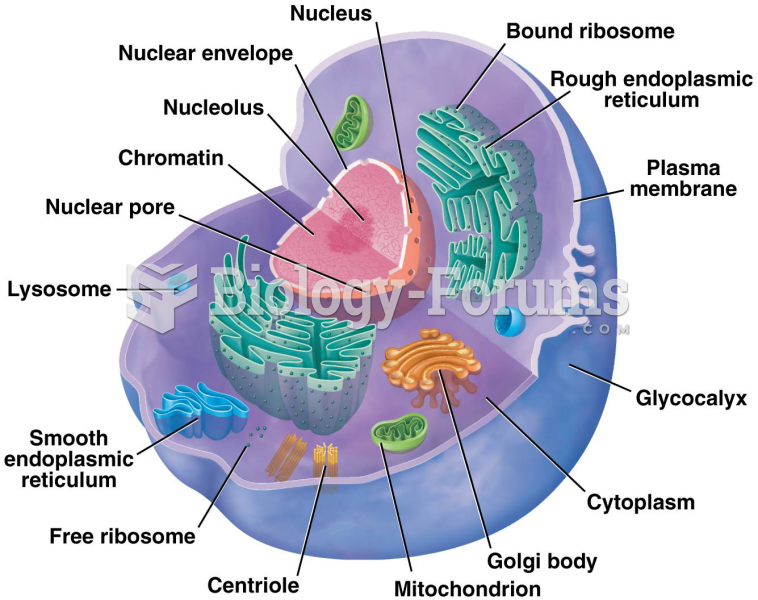
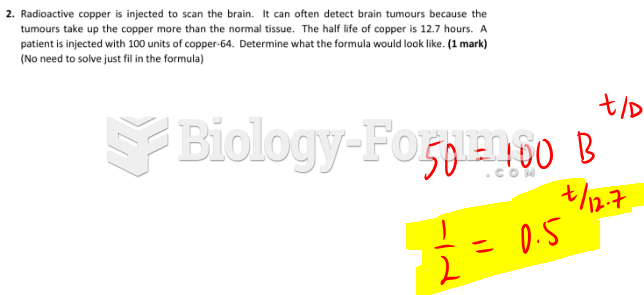
|
|
|
There are more sensory neurons in the tongue than in any other part of the body.
Colchicine is a highly poisonous alkaloid originally extracted from a type of saffron plant that is used mainly to treat gout.
There can actually be a 25-hour time difference between certain locations in the world. The International Date Line passes between the islands of Samoa and American Samoa. It is not a straight line, but "zig-zags" around various island chains. Therefore, Samoa and nearby islands have one date, while American Samoa and nearby islands are one day behind. Daylight saving time is used in some islands, but not in others—further shifting the hours out of sync with natural time.
The average office desk has 400 times more bacteria on it than a toilet.
According to the Migraine Research Foundation, migraines are the third most prevalent illness in the world. Women are most affected (18%), followed by children of both sexes (10%), and men (6%).