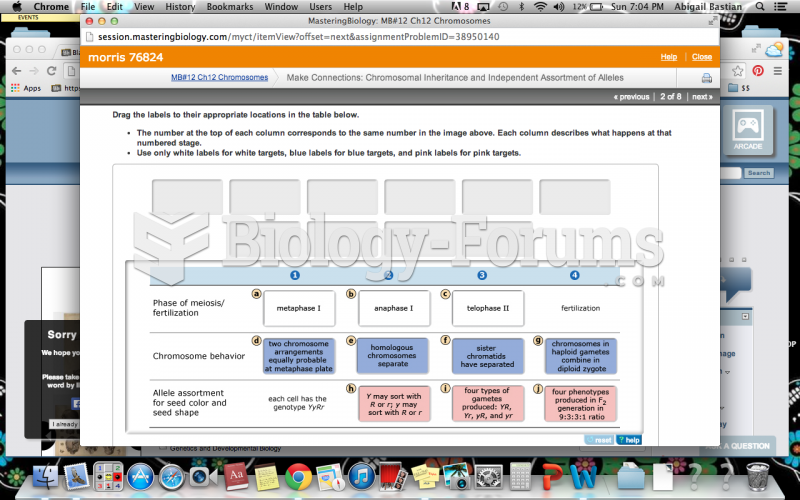
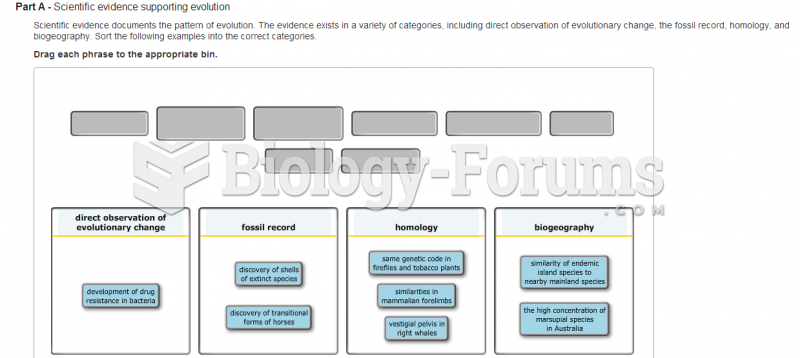
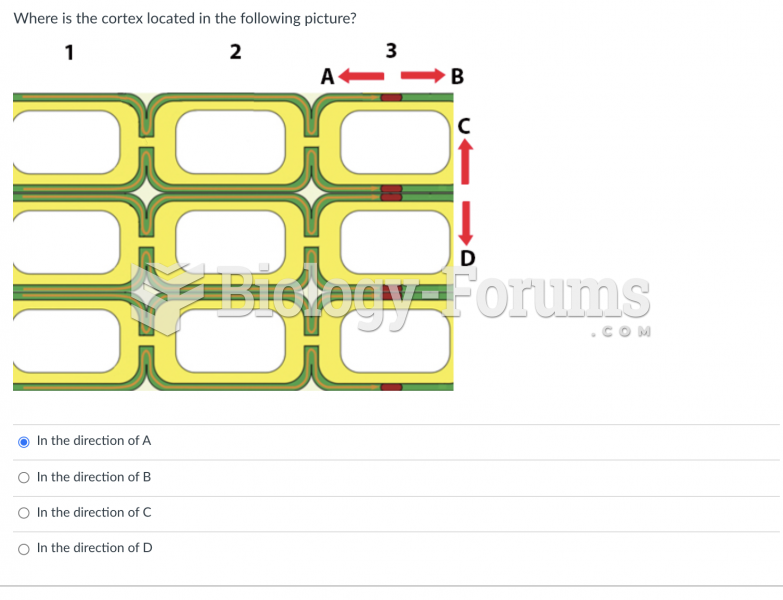
A high school biology student wishes to test the hypothesis that hummingbird feeders can affect the mean mass of ruby-throated hummingbirds in the area surrounding the feeder. She captures and weighs several of the hummingbirds near a science museum where several feeders are located. She obtains the following masses in grams:
The student's hypotheses are:
H
0: μ = 3.65 g
H
a: μ > 3.65 g
Use technology to calculate the P-value, then determine whether the data provide sufficient evidence to conclude that the mean mass of the birds in the area surrounding the feeder is greater than the mean mass of the general population. Test at the 5% significance level and assume that the population standard deviation is 0.35 g. Also, assess the strength of the evidence against the null hypothesis.
◦ P = 0.509; since P > 0.05, reject the null hypothesis.
At the 5% significance level, the data do provide sufficient evidence to conclude that the mean mass of the birds in the area surrounding the feeder is greater than the mean mass of the general population. The evidence against the null hypothesis is strong.
◦ P = 0.745; since P > 0.05, do not reject the null hypothesis.
At the 5% significance level, the data do not provide sufficient evidence to conclude that the mean mass of the birds in the area surrounding the feeder is greater than the mean mass of the general population. The evidence against the null hypothesis is weak or none.
◦ P = 0.255; since P > 0.05, reject the null hypothesis.
At the 5% significance level, the data do provide sufficient evidence to conclude that the mean mass of the birds in the area surrounding the feeder is greater than the mean mass of the general population. The evidence against the null hypothesis is moderate.
◦ P = 0.1418; since P > 0.05, do not reject the null hypothesis.
At the 5% significance level, the data do not provide sufficient evidence to conclude that the mean mass of the birds in the area surrounding the feeder is greater than the mean mass of the general population. The evidence against the null hypothesis is weak or none.
Details of plant population biology from repeat photography: (a) saguaro cactus in MacDougal Crater,
A young Lipizzan at the Spanish Riding School in training equipment, wearing saddle, bridle and long
master biology chapter 22-25
Branches of biology
Histopathologic findings in Crohn's disease. A high magnification micrograph of a colonic ...
biology help