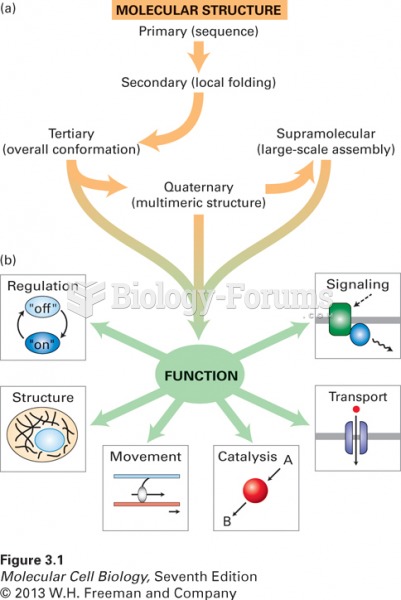
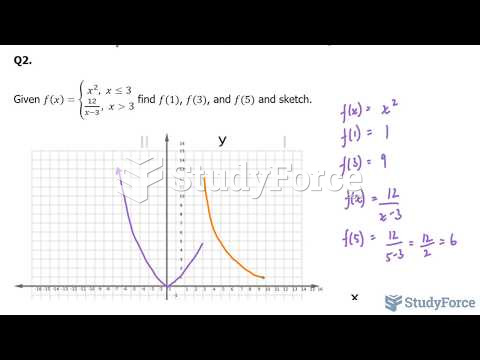
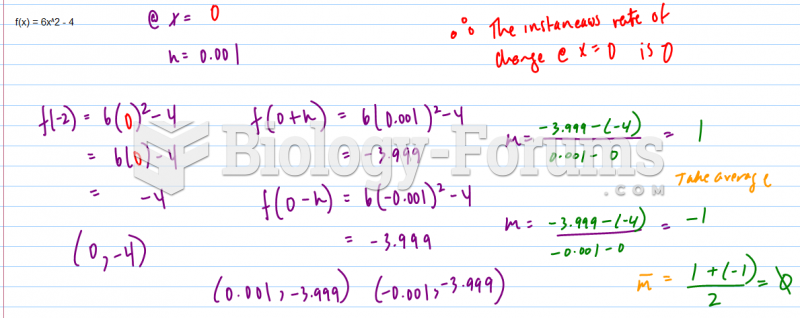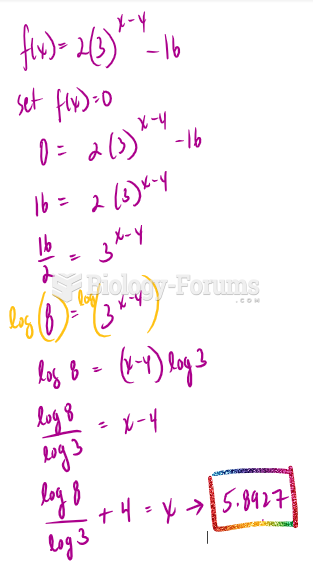- Grade 11 and 12 Mathematics (Moderator: geoffrey)
|
|
|
- Grade 11 and 12 Mathematics (Moderator: geoffrey)
Pink eye is a term that refers to conjunctivitis, which is inflammation of the thin, clear membrane (conjunctiva) over the white part of the eye (sclera). It may be triggered by a virus, bacteria, or foreign body in the eye. Antibiotic eye drops alleviate bacterial conjunctivitis, and antihistamine allergy pills or eye drops help control allergic conjunctivitis symptoms.
The most dangerous mercury compound, dimethyl mercury, is so toxic that even a few microliters spilled on the skin can cause death. Mercury has been shown to accumulate in higher amounts in the following types of fish than other types: swordfish, shark, mackerel, tilefish, crab, and tuna.
Street names for barbiturates include reds, red devils, yellow jackets, blue heavens, Christmas trees, and rainbows. They are commonly referred to as downers.
The most destructive flu epidemic of all times in recorded history occurred in 1918, with approximately 20 million deaths worldwide.
As many as 20% of Americans have been infected by the fungus known as Histoplasmosis. While most people are asymptomatic or only have slight symptoms, infection can progress to a rapid and potentially fatal superinfection.