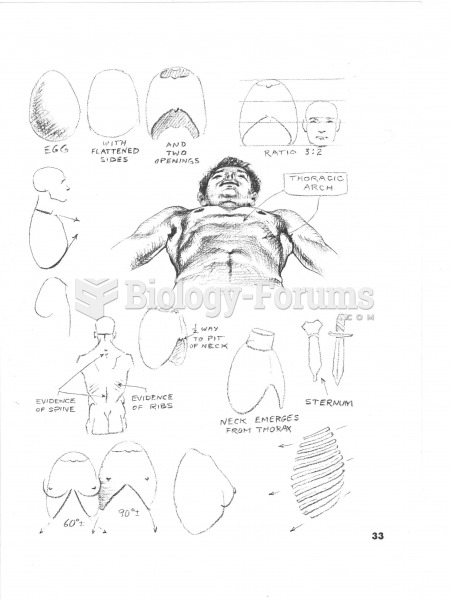
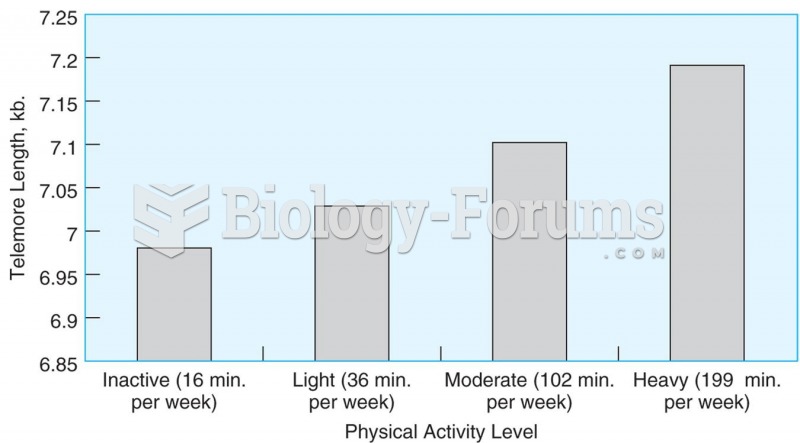
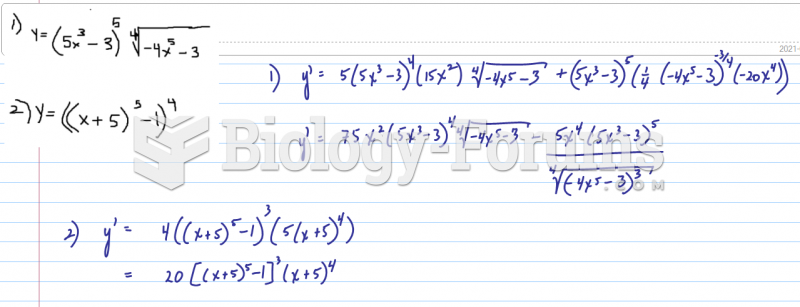|
|
|
Bacteria have flourished on the earth for over three billion years. They were the first life forms on the planet.
In the United States, an estimated 50 million unnecessary antibiotics are prescribed for viral respiratory infections.
HIV testing reach is still limited. An estimated 40% of people with HIV (more than 14 million) remain undiagnosed and do not know their infection status.
In 1835 it was discovered that a disease of silkworms known as muscardine could be transferred from one silkworm to another, and was caused by a fungus.
People with alcoholism are at a much greater risk of malnutrition than are other people and usually exhibit low levels of most vitamins (especially folic acid). This is because alcohol often takes the place of 50% of their daily intake of calories, with little nutritional value contained in it.