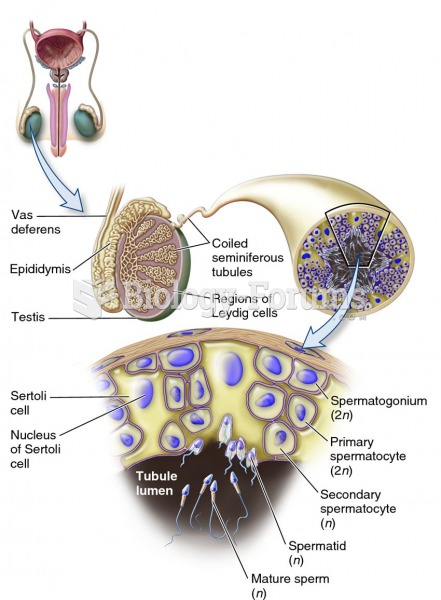
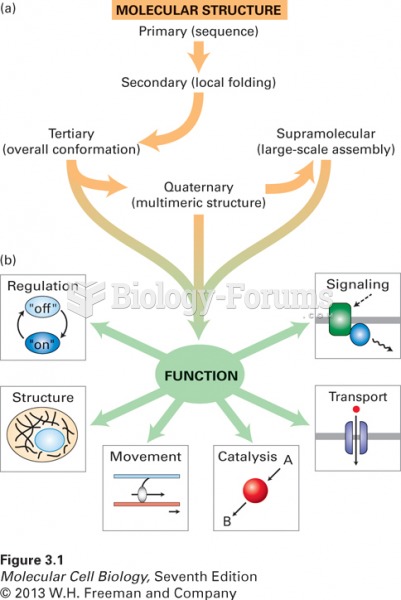
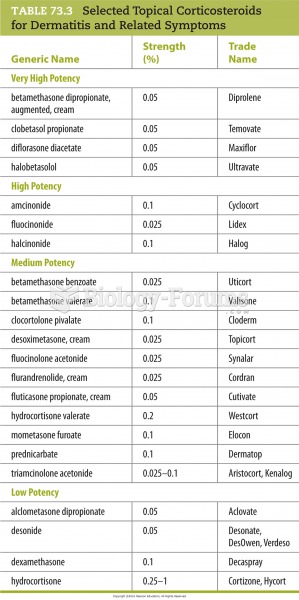
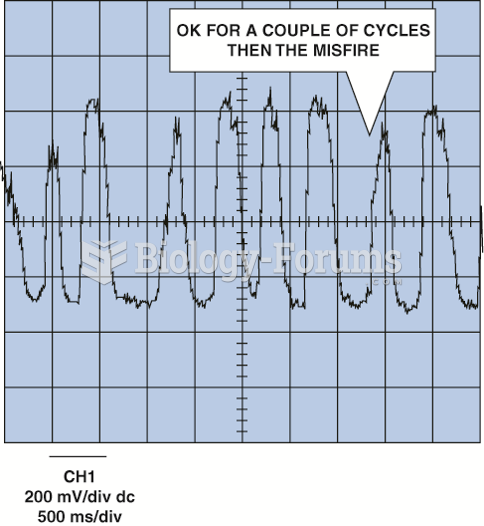
|
|
|
The Babylonians wrote numbers in a system that used 60 as the base value rather than the number 10. They did not have a symbol for "zero."
Prostaglandins were first isolated from human semen in Sweden in the 1930s. They were so named because the researcher thought that they came from the prostate gland. In fact, prostaglandins exist and are synthesized in almost every cell of the body.
The largest baby ever born weighed more than 23 pounds but died just 11 hours after his birth in 1879. The largest surviving baby was born in October 2009 in Sumatra, Indonesia, and weighed an astounding 19.2 pounds at birth.
Symptoms of kidney problems include a loss of appetite, back pain (which may be sudden and intense), chills, abdominal pain, fluid retention, nausea, the urge to urinate, vomiting, and fever.
Computer programs are available that crosscheck a new drug's possible trade name with all other trade names currently available. These programs detect dangerous similarities between names and alert the manufacturer of the drug.