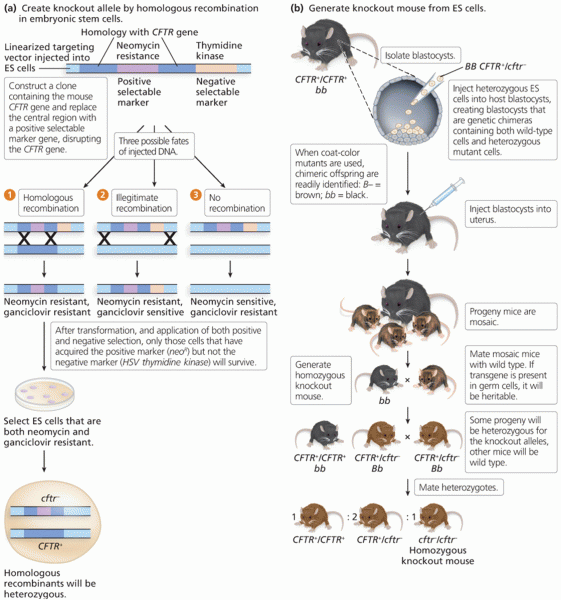
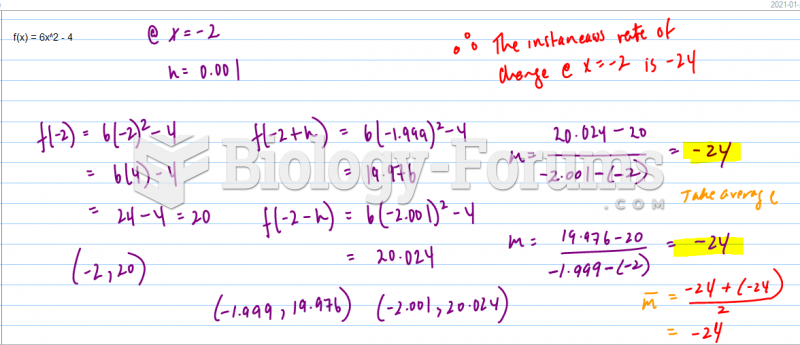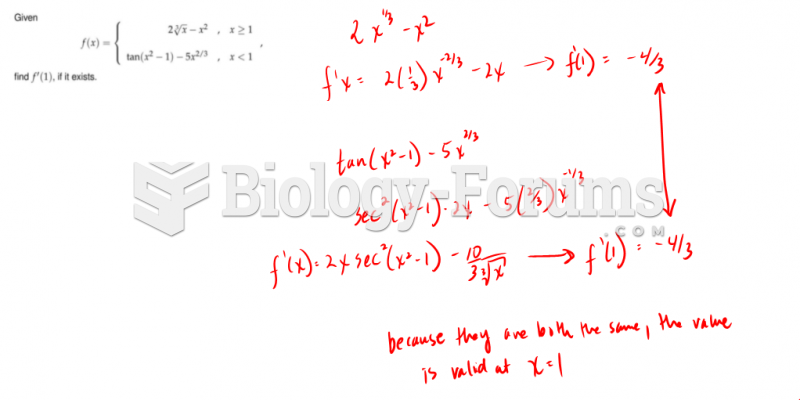|
|
|
Fungal nail infections account for up to 30% of all skin infections. They affect 5% of the general population—mostly people over the age of 70.
The most destructive flu epidemic of all times in recorded history occurred in 1918, with approximately 20 million deaths worldwide.
The Centers for Disease Control and Prevention (CDC) was originally known as the Communicable Disease Center, which was formed to fight malaria. It was originally headquartered in Atlanta, Georgia, since the Southern states faced the worst threat from malaria.
Since 1988, the CDC has reported a 99% reduction in bacterial meningitis caused by Haemophilus influenzae, due to the introduction of the vaccine against it.
About 60% of newborn infants in the United States are jaundiced; that is, they look yellow. Kernicterus is a form of brain damage caused by excessive jaundice. When babies begin to be affected by excessive jaundice and begin to have brain damage, they become excessively lethargic.