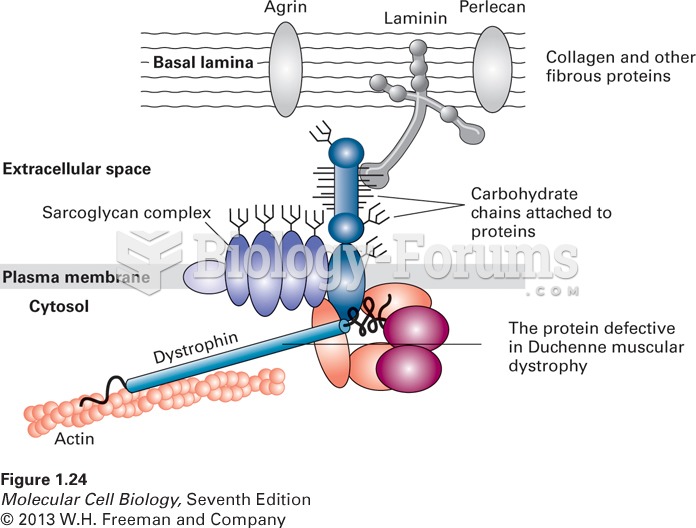
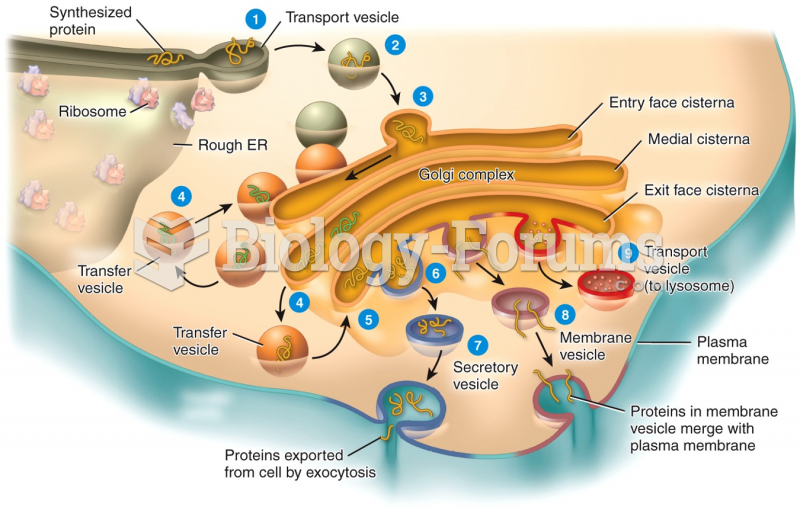
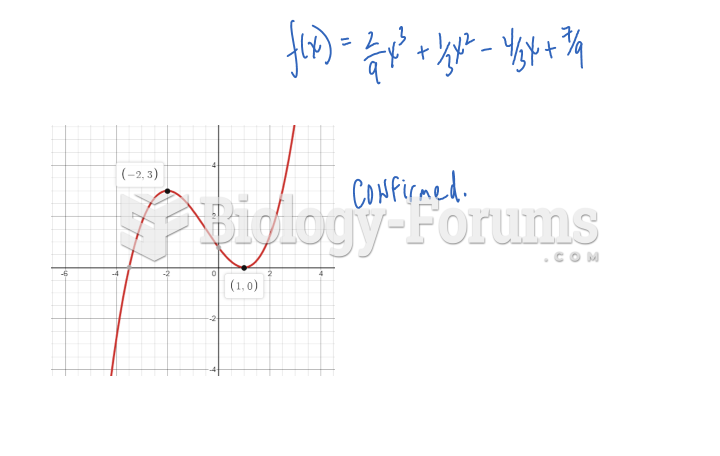
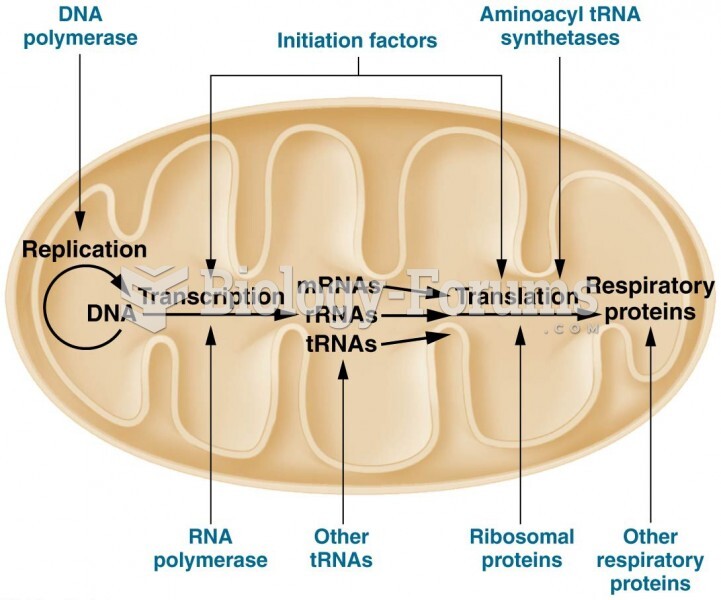
|
|
|
Cutaneous mucormycosis is a rare fungal infection that has been fatal in at least 29% of cases, and in as many as 83% of cases, depending on the patient's health prior to infection. It has occurred often after natural disasters such as tornados, and early treatment is essential.
Patients should never assume they are being given the appropriate drugs. They should make sure they know which drugs are being prescribed, and always double-check that the drugs received match the prescription.
Certain rare plants containing cyanide include apricot pits and a type of potato called cassava. Fortunately, only chronic or massive ingestion of any of these plants can lead to serious poisoning.
Individuals are never “cured” of addictions. Instead, they learn how to manage their disease to lead healthy, balanced lives.
To maintain good kidney function, you should drink at least 3 quarts of water daily. Water dilutes urine and helps prevent concentrations of salts and minerals that can lead to kidney stone formation. Chronic dehydration is a major contributor to the development of kidney stones.