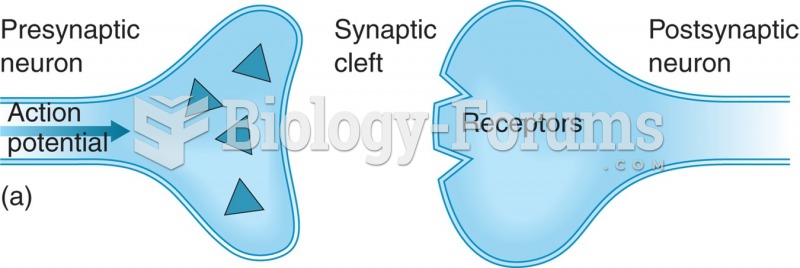
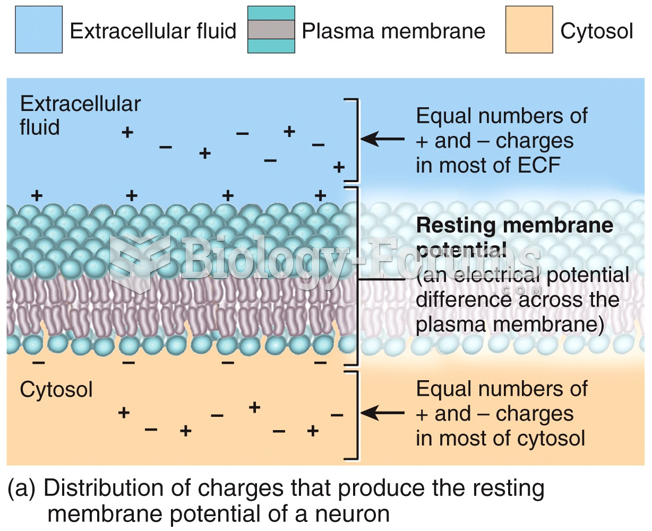
Rank the potential energies of the four systems of particles shown in Figure OQ25.5 from largest to smallest. Include equalities if appropriate.
 Question 2
Question 2x5BjSNIHnh0AYwA86kMY5IImRsNJ3rYakPI/ySydQev4phN/8BxTvfxBdb3wIvowS+Xxic+0N+Qyu0CgPg2cG8YH3fwDffPRRvPe978Ujj3wWW+s+e4t2ayHkGsh0kbbvy4zoU2Boeh4nR2YwMVdFLUkQ+B58D6DFHiaoKy7+RkV2bnoer07M4vuDYzjU340Hbu3DQFehrf9g2/c5boSWUzmJypPtyMwCXhydEQKkvPiS9wZkAw9hEMrfDQ2sKElQjRKMzJUxODWPY0OT2N9bxBs3JAhaAAAgAElEQVRu6cPerZ1X0ncboeOXaYPqj888/DA+9tGPSlWZz3zmEUm5apx0eR3TtvqlSWUy35ELMQ9NzeOl0VmMz1fAZx94HhhPTx2TCVIwK61ZJs5MlXBqfBaPnx7DkYFuvP6WPvQVaXQ3XbwB5KJPyxAhwfYQXXwVpSf+EbXhM4Afwi92CbOSgT0ycZIgjSOkUQzf85H6PtKQo8IMvGoV8ewMJr/6JZROHEPvz74XuSOvBezQdVEz2uGLh/PnzuEDv/5+fO+738Wv/av34bOPfLZpjT0PXIKIYczM+dGXCm3zmmmNz1ageeSVH9T6ImTb56FUjfDchSkMTZWE7HJhgA6PxQbUMiPN03KPSYBJAj8OVIA9D5k4ETfX8bPjODk6jQcPDOANt/S7dJH1fbjrcHfjyvQ81OIYLwzP4JWxOdTiFJnARy4TqAfeWPxJCkSeh8BPEMQQXUPDK+P7Ik/PXpzCydFZPHBrP960fwDZ0LjH1qFn135L1Qef/ewj+PjHP46+/n7894cfljJr9poMnOFSVHSVanI8f1msY5but+dufB1T7wrmKlU8d2EaQ1MLENdnJoAnozouvZRIKhpHg0KOSYow8RB4PgIfqMYeylGCxwfH8PzwDN56aAD37W2eqmsg0vzJEKEVTKOTPR/VV57G/Pe/hqSyIAToBQE8Eh3PJhMKCbJRAVI/Qup78k5qdHEAvswl6Zi1MnQaw1/4M/T+s/ei800/qz2WISs/NhNCc9M20mcPMzPT+J3f/m089thjeMdP/RT+4A/+s8x5TU1NynZ8fBy/9x9+D4cOHcJ//fSnzXyY9oHCKVZO41kv6RwxsGSz5Kd1+2raI1YPrXcPU6UKnjw7ialSVZRNEFA8+Z8ey3/pLk38FFHMEaKHGmIhOvmN1hw/ZIG5aoQvnziLsfkKHrp9F7Kh3zT/2A4ysW4Ppk1vrDIicp6qq6pUqeGpc5O4OFNGJvDE3Uk5078GnWWOUxpWCXyOBulMkstQXwVIQxEl4YKFWoyvn7yA4dkFvOuuvShkqdrsPdtDnv7+7/4Wv/+p35do8o9/8hN46KF3gIX+5eV5+JsvfQmf//zn8cgjj+Dee1sva9YgwjYSE/uY4GFiviw6ZrpcQz4TIKSbqT7Op7EdiH4JkhS+x3eCmpfIk05Bg5zaSGVoulLD3z4zJDrmbbftEK+VcJfxdjYjpERYFy4KqCHBx78KxBFCjgKDECRCmQMUj0bzaJBEGCDhxT3OHAExSS5J4MUBvCCE31FAUlrAxP/5KxHOzjf9nPZNyJLN2fiC+pdf/EvJxSkUCjgzOIh//f73o1zR6vDs+sJCGS88/zx+4Rd+QXpD4vyT//YnOPXyKfl7PH36tCwS+Zu/8ZuSRE/fNqNI9+zejY997GNS+aHxh9v8iNbrs3kmsiEJVnHszATmqxEKuRCh74srVFxY0kRPffZ+IiNCz0vhUXHJb5y78dWfH3hIUk8muCsAvvPqsFh4P3PHboScTKz/UaxXv9191wwBPlvREx4WqhGODU1gYr6CQpYKjxa9Gk9WG3AkyL+TiHqFSk80BfUM/Q4JEs5T+5xu8JETuYIQK9XgP79rj1xX5MlecM06ttoLexgdHcEnPvEJzM7OylTLF7/wRXz+f3xep6L4V+QBZwbPYKFcxvT0jNzwie9/H3/+F5+TylUXh4dRKVfw5S9/GUNDQ1KBhko/TmL8/LvehV9+93tMIzfYH5jlAE9JkDKxUIlQzIQIAx9UCTKQMGYN5UF0Z5LC49uGnqScR/ZkdEguSnwf+QywUE3x6KmLwn/vOLJTjPNWT0uIUOVTxSw6fwrzj39VFl0NOorwMhlxdcKMCOWJiGs0RhJHQFAT4eYIkLzMeTA/SbSsGM9JYnhJAC+XRVKtYurrf4ewpw/5Ox8gZbZq04bc17+tH/fcc4/8KbJ80ejo6KKxEB/WkSNH8ZNve5uMnFk2jQsWn3j2BMJMiG3bNGjoqaeekvkOHs9I0ltuuQWM9uoCi+huxJcqrR+dmxQS7MgE4r5SIaVLQv9I2XKOBuOUEX80gtQuo2yJ2koThKkvJEnyDD0PMZWfF+CJoQn0FHL4iYMmsGojwuDatEoEKCeiaURJP31uEhOlKjqyIbKi8HwxhHxfrXnejLqE7i+fcXiUJ7GTqGXUmApTD0mgMhWkqbhKkyDA0+cnJYLwp4/sFGW6yobfkNPDMMSRo0el0DanTybGx1VPNPlbGIvwwO1HcPDgAWkT1/t87LuPCZ6ZTAaHDx9GpVLFd77zHTUZPEgSPhes3ZCvJhKcK9fw1NAUFqqxyARd5NY4IhnKwzc6hjIRewnE2Db40GgKyUG+L1t6EoKEc8y+DMy+d3oUPYWMzCXrcG0xIppQL2t7+WBaxMzX/xrR1DiCQhF+Ng8vk4UfZgDO+zE0x77iGAkjRvmuVpDIuyrbtFpFUuG+KtJKBXEtkv2IIuHR3L796P+VDyLs3WnU5IY32aTXLIlWq0X2mVgkZMtnyj9iFuDOZrOyb2pqCqX5ktoy/Ctufplop2JnUXz+zT9tiM/sECet0wRPDU3i9OS8uJsoWNkgEKXFERwJjQ+Vc4RivYsLK0E1TiVIhoENjPyrRLF8p/++GkWoyD7uj0Ch7cln8S/u3osD/TafcgleGwIU14hrRkDkSc9+4eIMnh+ZFq8A55gpU1R6VH6c5yEVkjItEXIekfOHEkEaxagmCSo1lbFKrFGEDKevRKnMGdIQo2v0nUd24Z49TD5vB1nyUCrNY3Jysmn+bzHaxIMJ8Vu39sgP9CiNjY0hijj9sPjYxjcPvb1bxQvV2LcBPlkSFA9iiuNnJnB+egE0tDnHyxF+IHLh1d2j9KizVCWDqeQtgXgqFxVGk8ZW16i+YRqX6Jk4ksCavkIOv3T3Xuzt7VrCOzah3vMRTw2jcvJJRGPDOidI4pN3Fl42Cy/MwstwACmtQRpFMg8mMZAcAXDkF8fwA/pwfXiBr3OK/Ewrj/OLfFq+j9rwBZSOfRPdD72nzvQb4NFcoQkeBga2X+EY+zP/jIGenq3ytnuX3+rxy/++Xr+kkhbBwBix2mlticLyFo0K+Vgp1yRC+uw9WuqMJPYpzB4CWmccAYMjSLq5dM5UrH9+TlNwjueJwXHs7O4Qi1B6bMh4vXrv7nu9EfAwXarg1OisyBG9CjSkOA9E+cqEGvQg8mSI0I8TMFaQ/ia6vqhbRJ58usaSujyJlS+jBE2fqEUJjp+dkHD6rYWcdsQq3+VZ43p3eAXXU5LTyi9XOk31BYv3b9++40oHm983qI7xPJydnMf56ZIQoBjXEilsPU/qdarrGD53mUfWucAkjcVjIHpGgmasjiG12FQablPMVWp44sw4tnd3aEwCkTE6pj7EKz9/DJWTP5IRoAbGhDo3SDLM5ODn8/BzBfj5omy9XB5eNgdfXKc6h6jziL4mdbDl9TfTznTkYG+88OJTiIYH28RaE8R0ZGemZXUyi8LV6m1ls9VvrfbZ4zfQ1mNocoKXRuZk7i8QNyYJDTKXQ+udykuiRjMB8hn9zuWqRJhJgoz0M6RnhZJbun6sA4zfZQzgARdmF/Dq+GwDBCv9jT3uU1sjkOLlsTnJNRW3l0SCKhFSZjK+jgaYIJ0P1fOQCagQA2RYsEPmETk3rXOJDdlS9SKSxH9Mlg9dry9cnG4jxFrphlb7bJda/bbcPnvOBtp6nniHXh7Vv3nVMUZv+EyboYEUiI6hTEjahBjj+hsNKNExEq+gxjX1iugY6h0OwIysUMfQ8D47XcLgBL10NjiPeBlnaVqZR+WV5xCX5oT8RDHJSM6HL+kQoZChl+uAl++AbDlCDEIJoGFKhGT014mPDfANIzcaKHc0DBzPzaD84lMb6Km4pixFgDmCI7MLqnho3wiJMYydikiteSosFVJjwRnl5gcm8EEE0dhGIpi8C0eOKnzUW/xOceSIkoqyVuPcsQroZXw+S5vrvm9kBDxIlRjmhlEh8fmrUUR50kAZKj66xOge6wgpTw1DSr0HhvDoPrVKjgrOGFtyTcFAJhPFwTo4WZKRQJ0dxfDayEBtkrYZA3h0roLJharoFKEPQ2p0kZPkSHbUMR0ZBr80ZEKNIdVJcp4QYGNcRdlSE5tspuqE1MP5xVOjGmykoqJjQfk3ujiIZGaiERWqUiqCyihSRovSpcnRn8wbMoqU+7TlshW3p9r2cp74c6UlwtH6dPld9Bv/8VA79wrSEhslTd0kEtA+3aTPPkqZyCqmUZNh40slB5Kd5HOJNW8Jko+zoZzsk6UUWPdDY59iQQHlm2I3Nl/FxELVgGTIsH0gcy29DAIXpxdQriXqEaCMmL98tdp1pEdSzMhowEaRqlxQRdTVR/M9rDA17zOGFa87W6mJMSc/W0FbdKz7sl4IMP7g3NSCzN9RZ/BR8s1QlIaRBCFDeqAyQowqF6QeawDpmaorWoqDdFAm8UTHjM6VtctNB4tuqg29hCSOFwfDWIucWwoQyxsxkSeqSWoEGGAjgmW2cry5csq4LhMkJmW2lio0nTOszUwgmhpZr+fg7nsZBDjHMjJXEcNFn55GBPOZc9Le6hQmtjKBnqM5vrmfJy194jxn6UtF02pD/hH4EgGngioStPQU971NEaC6YIksyoiqFCsjDMgyMmW8AlqQgfKkdnML0amjYH+zOk22RnSoIHmtkdmykUvKmj2yfgn3YZ0QqESJ5Pg1PxJKRbN+oQxYHSNbUpFpr4iS/lPvwaVaxv7E566R7LWEATb0OlnTHLpCfeXsKXhBRhsQM+eLb5MryIikIEIa1EyuoCdEKNGiidYY5fHMGyQ5WqFuSJ4ZlrI9bLRhfhlpsobg5Aiw65DRhrbRbrveCDAyb2qBmX6qsFjOSHK2SHhcSSNhVRCqmgQxiynQ7WDr/5EYTX1IygNSjQIUojTiyN3NLxFJo6NYvJvn0Sq0MtN8rPvcfgiwytBkqabeIlF2Yltr7qkxpiKWVhMy1Mcu8iRGVqKFGixh0igXuSIOanyp3lHiJNEKF5pRw1w1FvXEKET32jgIMJKcBbTpCeIzE8OHz1bGVlqdioU5Kkgkl5RhU1EcS4EFKdxhjG8lRtUxi3hnSVeprTiK5It5rNkOygMVkYkarY2P6nyfCFfCUg6STK/l02oSqSWNTZj+oHXghAhrVc0lZD4hq4GTRIUQDas3C6w178S/L/+ocVbmxKV7bTQEKjGJLhXXpwgmE5dFYamfnXmjjBRmmrOfqFWvZY+43BSF2JZasyNFtfAbowHdz2tSNOs+/8BHRc5PNAdM5XajwePas0IEGO5eqkVyFkkrMQnQjATlqC3yWI5PCZDzgXqM1haVvDEp26fzyKKmTJQyU28oQ2pkKSmKb0HmDdXNxtB6iTZdYZvd4WuLQKmWSEAeS+XJ86N+oTwYw4hFFGpejCTVqRhSCA1syoO85blrSoWcT6NJDHcjD9ZwEqtbg2VoXFOllKoxtthKmDAjQi6lFOR9JTEpnRarG9TnKFAriHAU4LGGH2uK1muM1pDUqpJKoStQcIRIQlRS5GeaYhR6oXlyLx3AJr0ik8niiccfw5f/99cbI8W1xd5d/SoQYOrDwP4jGLj/LfBFUSUqoAmknJEv5dMSpMz7olw0pU/QitccH60Or0KrwkvlxnJZrDwkdpF43XVoqESowRHqar2KhrpD2gQBT+YGKRf886c3QdyfsRKgqia165kaIYVjmmvWGuWnrjGz6gCJkfa8KDslUP3McQNVDJUnk/QDzM3P4798+tOYnxw3S6W1CWw3cTPTJEb/waMYuPfN6gUQQ4fF1ulZYoBlQkcS+DQDVqkSY1uNHlvHmB4EfmYcg8iTIUaOxUSHkBjFo6DeJatjaGjxPH2ppa0l1kzdUGZ6JZEvuYBpJDOWciyJzA9IjrbWKP0XJLtI5gxTIUMm17MAd6RuUv4ub7aKn0XrgRVqhAgZKZYJcWHwAr76tcdkeOqM/40h+XEU4b4Hq3grhdSj9aWVPfiZSovuUIoRKzkwsmsREYpAW7cGXVJaco0WGxWZCKasTmErzmiQDYNueC2+6d5QenQSsTEkYvWtEAOIOoDuLS8Fa0VyqxVjdL6GPweSJyYMJ4UWRMGZJGqm89DQssYVr8lzLEHyM98UIStLoedL/AML5V88Myi6bfW9cVdYLQKsSnb/WxP03/2g1iamjjH1Q1k7lAqGDsjYpGtxJCczcFDSo1GlsqBkKLqlToicolNZoJ6S0muMVG7SMZQRdaCrptESayQqklgawJcC2jVhYh7ry91jxD5zBZl7oUIq84Ey8uPyS1V5S6WZOBJ3KQNrZOQoo0EZ0woBMuHeC0N5c9Ly7T/zs3jwg59Uk2616LrzrxMCHsYXIjx+cUGSliUVRsqmUSKoaXxxQdCyty5NETwjpFRUVGB0rdZMmSxRXlRiVliFICmmqSZXm/wgEiJXH+B1rf/+OnXKXWbdEEiRDVkWjVMn9DCpG1SMKto9ERPlgdhnWo0aVtRkdZJrkic7b0h5olFFchSSNaHxNLgkwlBWp9Br9XR14i8+9+fI0eW6bhi4GzcjwGd/dq6KHw6XhY/41+7FzC/WFzVDxmcpNRuB3hj902ziaLCuU4wXysoEdU+UJogZv2Cm56QQCKORzVv1S6NFQoR+Lifl0GRpJfprUYVvCI9uMlaMgV/T9AqeK+4ILsGkblBwHUJTbi0hobKkmowOZYwqFhmlWirTSF6ikiHCEF1925C56uoIjYa7T2uLQEe5hvjCK0jFTUEppehSBHX+RnIJbSKraYrO+6hbghYb5wpraSLvusISIdXRIYVUrHdxYZlqNSyWG+rSTWvbQ3f1G4lALgzFImfZK1/yjuld0FUDEhbM5npzpgKVKEPr5qJFb9a0pBFFOaKBpZ/1OxWgjjipPqlA6RLVBHwualLM57B31466kr2R/Xb3Wh4Bf76CY8OvmpVqKA8kHeNtkpKNrEVMY4a6h2axBtJQasTQphFkSu+Jt4CykTbmECVOIdW1UuvywKo1Rsc0t0yIMLt9F0ovPQ8/lxe/LH3tcmOOAiKSVqR5g9aisnM7MvqL1fUZRUhq6h4VEuQ6hSyzRVepEKknRMi6pbYajZ/NwevUunlq/Tc3zX1eTwRojeWCQAptq/XEeV6SoI84SBCwnBEteBFQCionqtWHT6XG0T5Xl5YRIRWXUV6MHhSLzVhq9Qo1ptYkLbbOHJUme2/tw/VEwt37eiDA59yVy+BCpSzrCqprSsvuS8AM3VbiYTAhn6IIOYrUkR/nlUmAJDzKFg0tRjbLqMC63emqN3Ik9UulmLeHYjbUVRycl+F6PMrrdo0cXeSeL2tS6t87WcAGSgWI/ViIkPqHJMia7apjaGw39Ah1CvWLeKC4NYYRR430KrBIg9UzrFJEUmSx92bOUSK89Q7MPfNDcV2K5U+/O+MBZR4whB/roruLFVOqI0I5hqPDGtKauliluDYjSGVUqPODflYJUEjQlGXzi53wt/RfN2Ddha4fAvkwxNZCVlYIoLBKPFbqi0IJUuNvT6xEWHtNFReJTuZtjOvK+vKlaLKQJC25WGYbWUJJ6kwaS40l23o6WLRcrylGotWa16977ko3GAEqn/5iDoMTcwg9qh2r8DiPTKPKlk4zk3wyT6zH2DUJ7ciPik5dY9b61yLM7JLKEgt4a0F4FnDuKWSbXO03uOPudssgkAoZUcecNdWGNBpYje0gNSRIL4FcQZ3aMmYkIRodI4bQIjcpZcIG0Gg6jpbpMyUgOfUSamnI5oYJEeZuvV2WW0rK9Nf6Oi/IyD7O5wUxYvpupcIMm2RCBKmhyLiMDDUuUnGVWreonXekwgt8+NmsjgSzrF3KIt4hwr6d8IpbFjFzc+Pc5/VDgBPLe3sKeHFkBlUaO1z7TaxzrQpP653rxImQNnGWnaTWeZtGYAMt+PoEN40kLtIrAqkCqpaah858iJ6OzPp13N15zRDY11uUNQhpEIlCC1JwKSXOA+lCq2Z+0LSAxzTkicaVUXJ1IjSEGOt8oi31Z2tScl6S5dr6bdFtua6q1TXrpLvwVSLgIRMG2L2lgFfG52TeOAn4vKlnuGSbygXjZuo6pkke7Pwx3eYyGkxi9RQYLwFHhxxdsjwbjes8K9OYBQO25DOaoyzjS5UHIcJwYC9ye/aj/OpLGvSShLroYUjXqFac4Qr0kuBsiFBClYUMNVXCzhfK1o4EZXkQQ4IkQJJhNouA73wHMrsPSSJ/8xD1KlF0h90ABA72d+J7p0PJ/0oD6KKXdGGZcmjiMq3779We4chRku/FXWUju+iuoEuL39WlQVdFs+JS5eVhoJhb7LZwo8Eb8KRvxC1SUXp9xZysIi+h8bSlKU82mo8r1Cxqis0H03ln9TKoa1RHhJCldzgCoEudoz9brJufqfj6Cll0cYVWeTkSXATven6hheN5OLitEz84My7LtIlxlNI44hqT9Dqx9osUpVUyFCJUmRAXqXic1F3OOWMu/cYRIqtikUztogB1mSAZBj62d+WtsqqvkSlEyFqinW94O+jSXDh9SgprM2GapMa8PyFAtqqulDhJyGtJCQAJhmEyPTWgzAsycZZzhIz4oUs0lwPnA2Wby8PPZBEO7Ea481Zt0Ho+EHfv1gikCbo7srhzxxZ85xUuQsxQZuYNaoi7BDYYebDqRS34RpoEFZd1Z0UpxIdPlwaFsSMTKhGaFSy4rzOXwa4thdbtcXvbHgGS0327t+IfTpRkBMAo0ZBRpCywzPB2mvlNM8NWnmzqjbjcqfxM5LF6GBJZ6osFmTuM9U+jKhv6KGQC7NlakHxCZ2xvQPFJU/QX87htWzeeGBoTfqF+EbngwMtEpS9tOQdh1jVqp2HERWrmj4UEfaNjMlzbkKNClYnuXAY765n01Fwqc0qEADrufD28XA4L//NPZTHdJBPKihJpwJGgIUFLhGRzvkiWzEGkANcT8Rkkk0h1+CCfk2syCMfjMk6yckUefqGI3MG74WWp9My19Iru3w2DAIXEw/17e/Hc8DRY/5PzhrJwqo3wW4YIKQ4UVlVYOrFNQaVCo4KyqwuI8qKgypI7Pvb0FLGl4Kz3DSMC17Mh/DP3Uhzd0Y0nz03i1Yl5WVEgYS5hokvmME+VL2tY8TNlhupmUZ4YCzvQXc/Rg6xWEdZliqtW6AjAx/YtBfR1Guv/evbFXWv1CBgO4iDrDft6cXJ0BtPlqugHDsIiSbNZ7Cq3NxV3OcNnbCqWGNm68DeP4UiwIwxREFngEnFGx4RqGBVzhvZE0FTatPgeR3ZBBvnb7kPXA29FvFBCUq5I1RhWneE7lXcVXH3evmUFeq5Gb97MJyQhcv6Prs8gn0fAESC3HR1ChEEui9z+owh3HjAk6IjQPuANt+WoMJ/FWw9ul8AWlshioVxZIZwrzJtV5stxAr51NWhuuTJ0Ku4OrkDPOSG+6ArlyuGirGjByzqGtNgCbOvMY9/WpppHGw4M16BVI5AC2TDE2w9vR0fooVSNVGYSyoquKk4ZsrLU2HL1cStPKl9UglR4xUwoIz/xMNDLYNbF3NqRxf7eoqyc4oztVT+5NbiAMiGnUno783jzgQHxHlEmqpGVAeoRu8q81S+x0SvcUmYSlGuRxB9wqoY6hjLRkVUCtDqGckeX6N6e1jrGSylRaWzcnj6S0izG/tfDKP3oGMCgFo9l1RhDo8xZR8SmUIjFpiHPXJqJuYKyXFNO5wJl8V6SIAkxl0N2zwHk73sb/Hxnvexaw+Vav7r7sN4I0Djiy4z6vnVqBF8/eUGsc87HUOjEZW6XxzH2jFhplAmJCtTIUObtcMKaIz91U6iQ0nKn4DJy7M6dPehmkIyMHJbI2npj4e6/egSsPIky8fDk0AT+/tkhUWCMKKV64RqX8mqSKR0RamoOPU8UR0aYNtxdHAHqm0qP5NidD3HHjh70cy7IzEWtvgPuCtcbAVmsQVSMRpt/7YUL+KeXR0wFGCsTl+qCukzIDJ2ubUodI4v4Zigb6hWQIBnqnQwjlvO4a+cWFHPW49TcG1N0u+GMSOAXutD/y7+BCS/A/InjIkecskwZw2xdoiKoyuh08PusOmMW8PVZNYbrFuaysoJ9wPnBvK5mn911K/J3P6gkKBE7S/wgzW1zn9cZAT5kK4Qp3nxwQNrzzVMXUY1Sk+dnyNI8RuvY4ml0cwV+KIqJ68vRJco5IioqcVVwhXuTKnFkxxaZj3SW+zo/8jW9vZUlvcl9e3tlKZxvnLxYz1X1PEYni3YzgXlUOTS4tOJMIAEwzAmjHGlwjCVEKjvKFnMVKU9CgrxVXYbXtHPu4teAgE2M4COnEfT223bIKiE/ODMmrm8JxrO6ZZGBbGqHSqCVj2xT7ij1DGUinwllS5noLWRxZKBrGRLUhuuI8JJ5Og/J3BRmvvE3mH/yMcTVii7OK5pOGyGOfK5CH/iSbG/LpnEruYKMECUJZrIIOgrI7LsN+TsegNfR5eYFr0FoNsIptOCODU7ge4Oj4FJJakBp8QUjTqLAGPgQchFNkxsoRCjEp+THHC9aawOdeRza1o0tkjeoNLoR+unacCMQEM2G5y5M4VsvD2N0vlKfG5RBnMkfozLkm/JEuWJQFT0S3NKjwKLaTJimUdVbzOJQfyf6O13swY14gtf1HvLQNTr4B4PjeGxwDHPlqjx71TAqL/Qc0BNVryVrZIE6RQ0kDYohAVLH7OjO41B/l6Rl6UCO8S5LW+6hNRGqJAJJDQs/+h7mnngUtZELEkVaL5pN15isXO/Bk3xDrR9aJ0ISYj6PTN92ZPffhcy+o0CYVXeos9KWPok2+G48Ap6Pocl5HDszjqGpkvjrrbLScGeNArSKiy4LEmLG8xGGXt1qZzTfvp4Cspl6vFYbYOCaeN0QMIqPWmlkdgHHhybw8tgsFmqxBmSZVW8YPk/5IgmKgUXr36xgz0lJI4UAAA8QSURBVG0m9NGZDbFzSwG39BZlDvq6tdFd6MYhQHngS7ghxenxOck5PTdVkrSruo4x6VqUBTGQjCxQ31AWJI0mCLClI4M9PQXs3VoUo6nubbL29iIOWpYI2SJmMtJn7yGeGUX5+eMov3wC8fgo0khXLqdjv06CUkw7A49zg7kCwr4BhLsPIbvnMLyiKaNm5wkWNUL77/7d4AgsenYsixSJsJ4am8PoXEUIUXughW1FULlCheTu6AiQI7+BzpwoLc7jyEsMvUtMtA0OhmveqhEQxWeqyLBYQxKLgXVydE5WlF9gYQ7jcxDrvynXkNZ+JvTAUPj+zjx29XSgl14FESMnS6t+NutyAXWJy63lEfqo1GpiHDHCeGyuLEE0HB1yRKhxCpC6odQ1dJVzBEgC3NbZgV1b8o38UatjFpFtcyeXI0Ie02Sx2bFksjCDaPQc4pFziKYnkFZKslaGBNQwT7DYhbCnH2HvDvhbB+DliuZudjTBr05Qmx9B23wWeVj67FgsOcHkQhVjcxVZ0X6Bq4Gb1eUprIzmY+1Qlk1jqSvOD9ZfIqD1b+7DZkKgLk9GAYpxTPlKMVmqYHy+gon5qowQmTBvrX/O/3TmsxJYxcjQYpbBfEvlcjMBeRP1dRHnNPrFKlWUh/H5KqYWqmJ0czlBVr+ijqGLnEUTKA8MuOP8YP1VlzPLaa1k5XJEWL+S/dDiAnEViKoSIejR7Rm0isixY1F7Hbe9uRBolgvmlWpCPZ+6dV+YUFDtNgWTL6e8FAf3bwsErEwpSZIIKTX0T1GmLh358Vd7TovLuV1tjkDzs6VMaMUq6hBxmZpgY5UQo19W1OMVEaFhVN5A2lW/+5JbXktDllzCfW0zBKwiss++WXCb5cbUqZWflxzTZj12zV1LBFrJkZUxe18zkuRXZ1RZUG7ebUsDmjrEygq7bj+vVLfU0yeuAj/bEDmUCq0ROq+7Vnrzq7inO6RNEDDPXnRVs3DaAu1N3XBKqwkM93FZBESn2TlEkp5Rcs3y0/x52Qu5H25eBCzxLTG2r6HDraNGr+FC7hSHgEPAIbA2CIiFtTaXdld1CDAy2aHgEHAIOAQ2NgLO27Sxn0/7t84RYfs/Q9cDh4BDwCHgEFgFAo4IVwGeO9Uh4BBwCDgE2h8BR4Tt/wxdDxwCDgGHgENgFQg4IlwFeO5Uh4BDwCHgEGh/BBwRtv8zdD1wCDgEHAIOgVUg4IhwFeC5Ux0CDgGHgEOg/RFwRNj+z9D1wCHgEHAIOARWgYAjwlWA5051CDgEHAIOgfZHwBFh+z9D1wOHgEPAIeAQWAUCjghXAZ471SHgEHAIOATaHwFHhO3/DF0PHAIOAYeAQ2AVCDgiXAV47lSHgEPAIeAQaH8EHBG2/zN0PXAIOAQcAg6BVSDgiPCK4HEJmKZ1r654vDvAIeAQcAisBIG11C9Wf63lPVbS1415bLgxm3Wzt4pC6ZaWudmfsuufQ+DKCFAXrOV4hHomdvrmCg/CEeEVAGoQ1vUiLmuZOTK8IvTuAIfATY+Aj2plDqOjp1FemIe3CjWjmsXol9RDd3c/+rftg+dnACQ3PZKr6aAjwiuitwrJbHltXq/5mpYYWx7sdjoEHAI3LQIe5mZH8cNjX8bw8Gkk6WrJinrF0GGaIhNmsf/APbjn3p9GEOZuWhSvR8ccEV6CoiUmJazZ6WGMjg4iiiqXHLniHXLpFPB89GzdgYHtBwwp8odmclzxld0JDgGHQJshkKYJnjvxTZw//xL8IITv+VeMRvBET6RyXIP27Ce7hYwso7iGl07+AL1bd+HWg6+vk2SbwXRDmuuIcFmYPYwMn8TxY/8X01OjKlnLHnv1P4io0lrL5nDbbT+Gu+5+BzzxhzgyvHoU3ZEOgXZHwEMc1zAxMQzfD+B5gXTIuyoq9OClNKj5PzUKXzxzsQ7hNZM4xcjoadx64LXXTYeZG95UG0eELR+nJ377Z55+FNNTI/AD+thX/7IiyyvFUYQXX3gM27cfwMCOwwDdIs0HrP527goOAYfABkeANnBapzNxGV1Fi1MkaYwkaZxJMm2pPzwfcRyZ0aBTMMuB64iwJTIe5ucmMD83aVwWDQG6WlFtdVkvBVJzKd/zEEU1TE5cVCJczSx5q5u5fQ4Bh8CGRkBVgW/462o1SwoOBrPZArI5nfdLkwTl8oKQ46UdTps8Tpf+6vYoAo4IL5EEFU9xMwg5XdlZccklltlhSZA/i9jz+o4Al0HL7XYIbAYEljo0L9/nNE3RkS/igTf+Irb27RH3aq1WwROP/y1GR4fg+culYjSM+cvfYXP+6ohw2ed+gwTnBt1m2W66HxwCDoG2QYDqgm7R6elh+EGAzq5+dHb2I5Ph6LDVqNIqGG75bnVM23R/zRrqiHDNoHUXdgg4BBwC1xkBj/ELFfzw+FcQBAHuufcdOHT4jeBIsfUk4XW+/016OUeE1+HBJkmMJObkdSyRW57nSyQYBZUCyncQOKivA9TuEg6BTYcA0ywY8EL9wglC6hfPp27h6JDRozrac1R47aLhtPM1Y+fBCmhHRxF9fXvQs3UngiCLcnkaE+PnMTV5ER2FTmSzHZieGTNW2zXf0J3oEHAI3PQILHZfkgDDMIOBgVtEx4SZAhZKkxgbHcTk5EWjU5y7c7Vi4YhwhQiqmCoJ0iQ7dOh+HDn6E+jq3r7kSglGh19BNleQDJ9/+tZfo7QwayK4lhzqvjoEHAIOAUFASY16hiTY37cbr3nN27F9122L8InjKk6dfAy5bF4yr8CQdDf/twijlXxxRLgStORYJv4wfyfF7Ud/HHff+zOyd3LiDIaHX0WlvACOEHftug3bth+S30rzEwh8Qu2cFyuG253gENh0CHhIkgi9fTvxxje9G8XOPkxNnsXQ0HMozU2iUOjBnn134Pajb0EclZGmdJluOpCua4cdEV4DnHSJ7tixXyw1SuDzzz4qyfGl8hzSJJYQ5i3dj+O++9+JXXvuVAIUi+0abuZOcQg4BDYRAmpoh2EWd9/9kJDguaFncfzYP2Bubroe+fnyy8dx/2vfiX233iuk6Yzs1YmII8IV4UeXaArf97H/wH3wggzOnH4SzzzzqExcawizXnB2dgpPPvkVdHcPiI9fJrVXdC93sEPAIbD5EGDVmATbevdi+85DqJRn8Owz/4j50hyydIMaQMrlEk48+yj6+vegWOw1ATP2182H2mp77IhwBQjq/GCKXK6Ivv5bZPR3ZvBZJEmCMJNdFAwThBnMzU3hiSf+HsXiFlQq8y68eQVYu0MdApsVARrbff17ZZ3CifEhzM5OIAgydRIkLn4Yin4ZHxtCsXOrDAgbdUc3K3LX3m9HhCvATmtAcESYQS5fRBSVUa7MSqqEDAmXXCvwA4zI8iopwiDjAmWW4OO+OgQcApciwPiDfEeX/LCwMCMGthagoimuL2uUl8uzdpeLQKgjsfIPy9XjWfmVNskZdD4kaYSoVkYQZqXmH0eErV48luTpU2obMtzqULfPIeAQcAjUEYijqnzO5Trr+5qViC3MpoRplYtzjTaBtaKPjghXBBdF0UOtsoCJiXMyMty58zA8T/36zZciOSYMf+7fgx07DspaY82/u88OAYeAQ6AVAkyYn5q6ID/19nIOsAdxHC9Kj6Bu4ZRLX+/eplxCJURLi62u7fa1RsARYWtclt1LIeWCl2dOP82xIfYffC32779PhDGqVSDvqCoBMocOvw4PvvnXcP/rfg65XIck4C97YfeDQ8Ah4BCg68jzMDZ6BnOzI+gobsWddz6IfK4gi4OzwHYUVeX7XXe9BcWufi3skcSIo5rD7xoRcHOE1wKc5+PsuRfR/9IPcPDwA3jdG96F/m17MTIyKOsMFopdkke4feftcvXTrxxHpbrg/KPXgrU7xyGwyRDgQt2l0iyeO/FPeN3rfx63HHgdCp1bMXTmhOxntapb9r0G/QO3IomqEjizd+9RKb02NjokUaebDLJVd9cR4Qoh1Dk/Xwjv6R99Q0aABw+/AQcO/Zi8my83NzOKl04+hldffUpcG7oSffMR7rNDwCHgEGggUF/0zfMxePpphGGIO+78SWwbOChve2RcW8Bzzz6K3q27sGP3URw8/OPo69+Hbz36V6jS6HbLu1mormrriHBZmJafeCYZct0vuimefvobOHf+RakF2N29XQJoFkpTGB8/C1pnc3OTcixdqpe8pGL8JXvdDoeAQ2CTIMBUCfGGSq0qDYGRrnvMWQZeeuk4xsfOYffu29Hds132zUwP4+KFUxifOI/e3p0YPPOMeJtKpWnUosolJMh7sAiIM8SXFypHhJdgQwLkdDMrPFzy46IdTKynkI2MnMHoyKDk/cipRvDAVSiCQAJsFp1ov4jVdoWb2GPd1iHgELjpEKAKkKJTLSpPkbg8L8DExAUhPWtMC3kCYHrW+Nh5jI6eFRqlvlm6yg1Xr5d9boR4WdlxRHgJPBpzRQvqSkzIiqMU1iDgOSmQ0rHBZVLIo1cDLS012wBLwPa72zoEHAI3LwIp/CDEwLZ9mBg7hzRknvEyvaVBbX6ilvCFPY2u8T0EKXWNjixVb+nBjFz3fQ+7dt0uhMrgPjXyl7nPJt59Ndp6c8FjXBW0okh0SobLSajQngiXHEkLzpyjZ9rzl4GQ6xT6VsSXOcbtdgg4BG5KBDjCO3rnW1CulHD+3EkJcmmpaWSn1SXNWwPLopPUsua/+Vwetx95ALv33HFFo/6mBHgFnXJE2BKsRGqEbtu2F6dPPyNVYYTf5NhFUicjwMYllDr5nYKYIlniFlUh5cgxjmsoFrowsH1/43T3ySHgENhECLCCzBY88MZfxOTkBdSqnN9brvvNBGj0yKJD7e+6k/Z8oaML3T07zVE8Z9mLL7rSZvzipeJwbgXsZoTD9pl4+JifG8dTP/x/srySwKSF4e1BK95qRJi6NDqLPbjn3ndg526uTmEr0zhBXTGo7gSHQNsjsNZ/906/X15EPDgivAQhKzQUTg9pXMXMzBiiuCrrEC7vyL/kQpfs0JgwdZ52dW1DNlesjx314LX+g7ikSW6HQ8AhsCEQaNY7G6JBm6gRjgiXPOxmYbSf13IOj/fgmwRot0ua5L46BBwCDgGHwBoiUCfCNbyHu7RDwCHgEHAIOAQ2MAL/HyOu4Fc6oGZWAAAAAElFTkSuQmCC />
1.c > a > b = d
2.b > c = d > a
3.d > a > c > b
4.a > b = d > c"