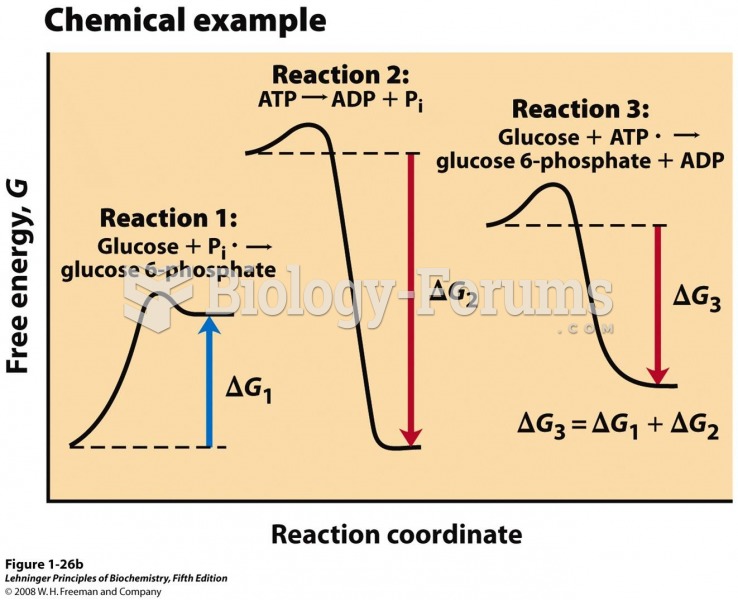
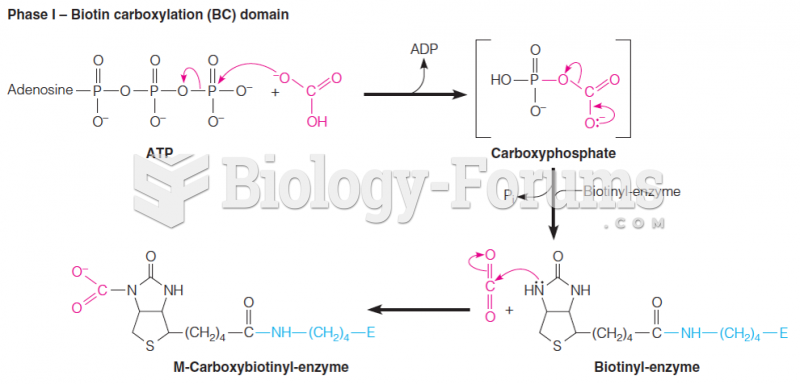
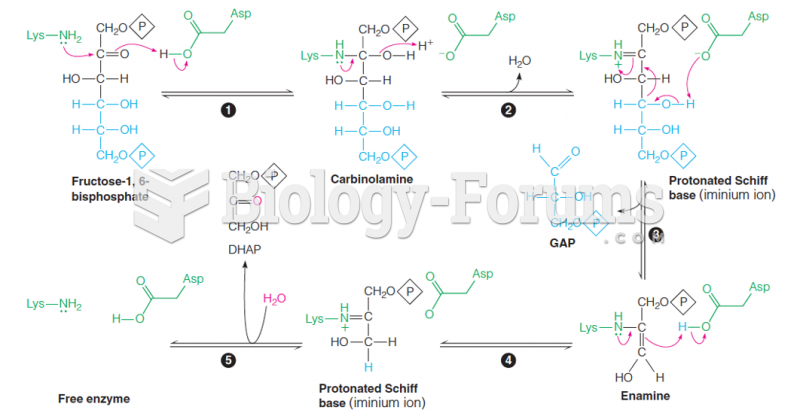
When a student ran an asymmetric dihydroxylation reaction using cis-stilbene and the ligand (DHQ)2PHAL, the hydrobenzoin showed an optical rotation of 0. Explain this result.
Question 2M2c8hqt3W61fv56tkPaoEKIMbGKHp3d2u2frXW4R8tbXTelCZGZYm9VREfHkIlpTz4d6qGvy7j27Iz6EkAp6jO7jj7eowSL+qF3CZkbeVnvblQ9Wnqt/nd3jLR2THnf38Zhw94ynJ+XKl3VklABv50SHxSpUuKCtj6K3eswPHgE84UFoWghPPCWBe11SCY/FtZjHDx5mqsKVEDO4WPE7kn3ErQW1N7swwwS3PUQ58CfpdpMS9Lg+6ag3ujwFvT+UWTbWCWD3Udycuy4gdx3z1GlT1fUIAjISCdHxYJ+3QCHaPl8nQCIxhlD0qT01cH3DhkzRlvQT6Yd69XSE6SEX9BglZpiwUMwu9jx87bE7ZLjdO+DrhB9HuxXw+kvmLSa9I85cGIzAQiMwwjoCuwTftzuKFVXRgRAhKFx/iGHr7fHps889q2xOTkTajYd5wSOA2YqEXDnVucB3CO51c+fNNfCdwYJU7ND6+uuvG/e0vkf90KEMbux93ZApWJZiYRpc6uC7ardIzZd+cL3A0zzclCDyhj8J48ZfUoIe7SHqjZ6dR3kKen8os2w8EHjssUfV/yW7J26YAceNe8FCtxvhjuCG6wPc5bwF1tBPEOD+G49Je2pgciWaEiZxatas4ah9lVIBoIQ4mX7MUrZcGbnvvvvk/xYu8uht1aqVcvLUKRk9arTHsVBlbNnykaxYsUJmzZotqVOnTtSNGZNezP9cMmHCU/LkE08mOhZPH/DVMGPhyvETx+XzEyclZ86ciYZvzsTKhKfGi3nBSpQf6g84X5MmTpYCBQok6spchCnmphVSsUJF+eijLZIqVapEx/khvAS+/PJLeWTgI2K6oCTbcalSpWT+/BelTu06yZYNdgFzUkGaNmsiGTNklKVLl0n+/Pl97sJclCf9B/STNWvWyIYNG6X6ndV9rouCpkhX5ceNGy9jx4xNsq4ZEULMIAKqTJs2bWXF8hVJludBEognAuYMr7r+Z8+eXQ7sP+jxu75mzWoxJw5lzJNjZPz4CWFDY4YzFPPJgbzy8gLp2bOnR79mNCt1/Th+7IRf1x6PhqI4w9ypXhYsXCCHDx2REiVKeIzkm2++kUWvmtox9HI1Ud8ZMmaUQQMHSdq0aRPl44M5ISW9+/SS6dNnyKPDH/U4HomMsAh6DMzcsEkmTnxKduzYKdWqVovEWH3q04xDr24+brrpJjl65DNJnz69T/VitdDefXvFXOwhvXr1kpdefNnRwzQXJIr55EX27N4rlSpVcrSt8WScGflFVpo3zzt37pQjR4+IGc1GDb9cuXJSpUoV6dihozRu3ERuvvnmiGGBqO/6QFfZZ37fJ02aLL179ZY0adJ4tQc3u6ZrkIwZO0bMmRpzfKukTJkyXst7O2DOzKtD9evXl/r16nsrpvLNqDdiLpjDU1UpWaKkmiBJsgIPkkCcEVi0aJH0699Xnn32ORkyeEii0eP/TbfuD0q2rNlk9uwXEh0L5YfJUyara9+6tesEusI14dpobsRpaqNJYZ3QdLXBCe9xbTPDPsqd5oTI+nXrPUwyXZFMDfKQuvZ5HAxhRqZMmWTzpg89JjPNPW7UzWOWLFnk0MHDSf5WhNA8z6bNL3lYEjZsgksGYs87eUWz3qly5coVYeESDZ0gcgce8+/bv8+x5mpfNnO21LE20jBnE8CjcewonDtPLvWH79LSpUsNuA/BTQjRDMxZPgOPhuFqBpc87HWADcwimcwnIQY2NWEigXgnAG1RvfqdRrbsWQ3suOzkhHV8cPcrXqKYAZegeE8vvfyS0hnRcC0bOXKEsvX9999z1GkLiw+9HjFEMoSh3SYQukwkXxHiELtHeotJH0nbItk31j5gkSOil0D0OC3hIo7QV7iII9QoU3QSwHcLax8Qfz2SCfHwTbc7tbFT0TuKJPJdhx8sFr5C+GP9jxOS3lznuZnPOcEc2kACESWwY+cOpTP69usTUTuS63zhwoXKTruw3snVjcXjuMFBWF5s0IT9BZyaTp48qaKZYf2X01JYBT1+sBGDNdKx572dhM5dOnmNSe+tTrzk640TnHgzhpBXuFGcNXtWvJyOmBzn1atX1Xns3qObo8aHMHKINHPu3DlH2aWNwQ0IFsni/wBFvabC13gmYLrWqP8PTn2qjGtdrtwJanLAiZNkkfrubN22VZ03b1ERI2WXa7/YZwThifHU1mkpbD702tnHjMEqlatUkvbt20vXLl11dsRfjx8/rvxh+/frL3PmzI24PU4zAH7P5SuUE/i6zTX5OGVtgRmZRAYPGSwJCQly8MAhj4VQTuNIe5ImYM6qiXmDJtu2bfd7gWnSLTvr6CeffCzjxo2TDz7YZLvgyl9rzZsO6dyls7m4brXMmPG0DB823N8mWJ4EYoaA6R5nBUj4+ONPHBcg4dFHh8v8F+erRaDFixePGe7BGAjWOaxdu1ZOHP9c8uTJE4wmg9aGuceNtG7TWi2CxWJYp6WwC3oAaNy4kWCRg9PSLbfcIt+cvyBYJc/kSeCVV15WUUs8j0Q+59VFr8kDDzwQeUNoQYoImC5T6oe4RPESStS7LyJLUeMOqYybY3MDGcmQIYPs3rXHY6FcoGZC1Hfp2kUt1nVS5AWMx/Rnlo0bN8ru3bvkOzMalTmzpYaZLVtWtRCuRfMWcvvttwc6dNYjAQ8CpiuamBskmhNQ89QEokeBCGWcPn1KTLdeGTZ0mEybNj1CVji3WzP0r5QuU0ruueceeX7mLMcYiuu2ubO4XL9+Td1sZM6c2TG2aUMiIugRXmrLli2SkCtB2xHxVzM2reRKyCUVKlSIuC1ONmDVqlWSK1cuSXWTM0JCmo8r5crlK9K6dWsnY6NtfhAw9z0QM6a0xOpNmukaJuaukfLhhx9Jvbr1/CCTfFHXmXoniHo8+Zw8ZZIKEZw3b14zokcDyZsnrzWQS5cvya5du8TcGEiaNWsuY8eOjeknM9bA+SbkBMxNBiVf/rwCveG0lC5dOvn2wndy6623Os00R9gzYuQIef75mY6wxd0IhF7v1q2be7YjPkdE0Dti5DSCBEjAkQQgSuGW99NPP6mZEIQOi5WEmWrsldCsWTNZ+taykAzLdaZ++TvLpW3bdlY/5sIzeeedd2TFyhVy6NBBMTe1Ucewx0RVM5xwq1atpEvnLikWGpiBnzZ9mhkCdKLcdVdDGTlihNSv38Cyw/3N0aNH5YU5s1Vs5759+srMmc87JxScu7H8HDUE1q1bZ95MLpeKDgpj/NlnR6VOnbrSs4dnTPqoARtiQzHB+pAZphJhjZMKHxxiMxI1f/nyZbl08aLaL8WpT44p6BOdMn4gARJwAoHNmzdJi5YtZNTIUSouvBNsCoYNffr2NjevWirHPjsuBQsWDEaTtm1A1JsLy6R9u/aCTbuQtm3fJn379pHTp0/b1tGZOXLkkOnTZkj37t11ll+veDRtLmw2N3f7SBYuWGg+Ovf96Rn2vehqug3ly5tPVq5cJdmyZfOrbxYmARIggXglQEEfr2ee4yYBhxPAro5YhIQN3ooUKeJwa5M3b8/ePWLuw6F2n8Yu1OFMWGg8aPBAgRsC1gp16NBBWjRvqVwMsaHXmTOnzQW6H8jSZUstF4UnRj8hTz31342v/LEVG/usX79eNn2wWUqXLu1PVVUWPrTNmjc1b3gKyep3V3Ohu98EWYEESCAeCVDQx+NZ55hJIAoImBsmSbnyZaVFi5YC15FoTljrUbduHfnmwjeCLd4zmluKhythZr5582ZKzGNb9TeWvCkVK1a07d7cc0Luv/8+2blrpzq+6P9elQcffNC2rF3ma6+9ZkadGiS7du4OSMzrNhGlpGKlCjLUXDiIGwsmEiABEiCBpAlQ0CfNh0dJgAQiSOCppyaYiyonywcbP1C+2BE0JUVdL168WMwdl+X11xZLly5dUtSWP5VxI1G9xp2mv/whFUVm3979kjVr1iSbuH79utzVsIEcPnxYsLU5wsfBxz65ZMbqV9u3I3IH/OBTmlavflceePABOfn5KcmXL19Km2N9EiABEohpAhT0MX16OTgSiG4Cv/32m5QpW1oJS4hRuItEW7p27ZoKw1a4UGH59NOtYY2JvWXLR9K0WVOFzJ+bCXO3TTMiTX0VXnLKlKky4vERyWIfN26srDbj4B86eDgooTixsLZmzRpSr149efrpZ5LtnwVIgARIIJ4JUNDH89nn2EkgCgisWLHC3DSpk7zwwhwZ0H9AFFic2MRRo0aKuYOr7NixU6qZkWTCmR5+eIAsWLhARa1BmDyEy/M11a9fTyDs4Z6zd8++ZKsVL1FMBg8eIgMfGZhsWV8LYAHx0GFD5OuvzgdlAy5f+2U5EiABEog2AhT00XbGaC8JxBkBzNQ2adpEjhw5LJ+fOBlVkU9OnjypfME7d+4s8EcPd6pRo7rsP7BfGjVqLBv+s8Gv7seOHSPTZ0wXLJq9cvmq2gjLWwNnzpxR4Ti/OPulFChQwFsxv/PxdCMhV07ZunVb2G+G/DaWFUiABEggggQo6CMIn12TAAn4RgBxyqtWq6Jm6GfNmu1bpQiXwo3I3ffcLdvNRamR2sY8e45sAlHcv19/mTNnrl9Eli1bJg92++/uywf2H5Ry5cp5rQ9/9169e8nlS1e8lgn0ABbHDnxkkPTu3TvQJliPBEiABGKeAAV9zJ9iDpAEYoPA0KFD5MWXXpT9+w5I2bJlHT+o995bL23btZXJk6eYGyuNjIi9qdP8d83B4489LlOnTvPLhnffXSX3mRFvkJJzF3rp5ZcEPvQ//nAxUR+6/0SZPnz468bfVqlmZoSeOnXqyNgxY608viEBEiABEkhMgII+MQ9+IgEScCiBq1evqigqFSpUlI0bNoZ1cam/SBDvvULF8vLPP/+oOPr++K7721dS5bWgDkTQr1q1Uu7vdL9qfteu3VKlchWvXcHXfcjQwSER9HXq1Jb2Ztz84cOGe+2fB0iABEgg3glQ0Mf7N4DjJ4EoIoAFnljouXLFSmnduo1jLccurU8++YSKn9+2bbuI2VmyVAk5e/asuZFUR1m2dJlfdkyaPEkmTvzvBlhXr/wkmTJl8lofTyN69OyhBH2qVKm8lgvkQIHb88uzzzxnxsf/781FIG2wDgmQAAnEOgEK+lg/wxwfCcQQAcx416xVQ3766Sc18502bVrHjQ6bIpUqXVKqVbvT3C11U0SfJPTo2V3efPNNyZ8/v2DBqj9iu9XdrczdYzcKNqP67OixJDmfO3dOihW/Q5VD+WClS5cuSZ68uZWbVfny5YPVLNshARIggZgjQEEfc6eUAyKB2Cawfcd2FSPd1/jo4abRvUc3gQsK4uZHWoSuW7fWdFdprxCsXbNW7brrC48vvvhCxc7HDRRi0IN1cqlwkULy6KOPBTVsJRbmDn90mFz45lu/bkaSs5XHSYAESCDWCFDQx9oZ5XhIIA4IQDSvWbMmYtFjvCFG3HbEb+/Xt5/MnTvPW7Gw5f/9999SomRx+frrr6VkyZKy9dNtcttttyXZP3aX7XhvR8HNQOrUqdWse5EiRZKsg4Nwz1m+YrkcOXw0aOIbC2LvKFpU5s2bn2z/LEACJEAC8UyAgj6ezz7HTgJRSgBuLUXvKCJp0qRxVFz6H3/8Ue1me/bMF5IjRw5H0N24cYPc0/oetesrFrauXbtOEhISbG3DYt7efXoJZsaR/FlMe/HiRcHmUvPnvSiIu5/StHnzJmndprUgZCZuRphIgARIgAS8E6Cg986GR0iABBxMYPjw4bJn7x4pXLiQY6w8fvy4KWa7yGOm64mT0tx5c2XYsKHKJNxoDBo0WFo0byEVKlSQm266SbAx1CZTQM+fP08+//xzVa5Jk6ayft16ddzXscyZO0cmTBgv27Zul1KlSvlazaPc5cuX1b4Dne7vJNOmTfc4zgwSIAESIIHEBCjoE/PgJxIgARKISQKYdUdoyStXkt786ZZbbpEhg4coIe3PIlpAg4sPYtefPXvG3Jl2o+TJk8dvlr/88ovcbS7I/euvv+Tjjz9Rbj9+N8IKJEACJBBnBCjo4+yEc7gkQALxSwBuMdicC/7xhw4dSgSiUKFC0qplK+nff0CKXFz++OMPade+nRw+fEhWr14jd5rRfnxNJ0+elM5dOim3pY0bPpCsWbP6WpXlSIAESCCuCVDQx/Xp5+BJgATilQBmwrFYFgk+9cH0+b9x44baOXb2C7OlY8eOMmrkaClTpoxX1BcuXDAXvs6VWbNnSdu2bZUffnKLd702xgMkQAIkEIcEKOjj8KRzyCRAAiQQDgK79+w2feonCBa4Vq1SVerWrWvGqy8uCTlzql10Dxw4IDt27BBEB8JxlG3cuEk4TGMfJEACJBBTBCjoY+p0cjAkQAIk4DwCp0+flrWmm8/u3bvlm/Pn5fw35yVLlixSrFhxqVSxojRv0cIv1xznjZAWkQAJkEBkCVDQR5Y/eycBEiABEiABEiABEiCBFBGgoE8RPlYmARIgARIgARIgARIggcgSoKCPLH/2TgIkQAIkQAIkQAIkQAKKADYozJc/r3q/ZPEb0qlTJ5/IUND7hImFSIAESIAESIAESIAESCC0BCjoQ8uXrZMACZAACZAACZAACZBASAlQ0IcULxsnARIgARIgARIgARIggdASoKAPLV+2TgIkQAIkQAIkQAIkQAJBI/Drr7/K8RPHxTAMKVe2nKRPn14CFfRohIkESIAESIAESIAEQkrg/PnzxujRo4zatWsZ2bJnNW5JfbP6K16imNG9Rzdj1+5dfvXfvkN7A39btnxkfPfdd8awYUONPHlzqzbz5stjDBz4iHHt2jXV5uXLl43HH3/MyF8gnzqeK3eCcX+n+w1zjwTbPg8ePGj06dvbKHpHEcvOArfnNx54sKvxyaefeNT5999/jffeW2907tLJKFS4YKI6HTp2MN58803jn3/+8aiHjJ27dhrduj9oFCla2KqH98jDsUBSUm3u2bvHo8m///7beOedd4xGjRtZ5wbnCJ+Rj+PuKRT827VvZ+Bv/fp1xrlz5xSD3HlyKS54BZNDhw65m2J9DmQc+ns4cdJEqx33NxUqllc2dOp8v3VIj//tt982rl+/bkyYMN4oU7a0dQ5r1KhuPPvcs7bn/dSpU+q7mz5DOqt85iy3GkOHDjHOnj1r5S1dutTqL7k3FPTJEeJxEiABEiABEiCBFBHYtOkDSyhCQN1esIBRrPgdBkSMFlRp0qZWwtfXjnQ9CClXMazz8Vq3bh3jq6++MsqVL2v143ocAh/Hdfrrr7+Mxx571Eid5harfOEihZStuh7sfOSRhxOJ3AED+lvl06ZLo8pjfLoOXlu2amn88ccfuivjl19+MXo+1CNRGfSFP9d6/Qf0U2Wtikm8QZtdunZOVN+9Tdg3cuQIq5UffvjBaNiooVUH58T93DRv0dxAOdekbQwmf93m4MGDrJuznAk5jFKlS1r2Zbo1o/HKgldcTVHvUzoOfwW9thUivFatmpZ9Ol+/4gbFNeHGFWPC8Sy3ZVY3MLhR0Dejrt9VCnpXcnxPAiRAAiRAAiQQMQIXL140sma7TQmYu+5qoGbFMaONdOPGDWPhwoVGhozp1XHMgtvNBtsZrwVTxkwZjIqVKhhr1qxWgvnChQtGj57dLYEFoYQ/zDRfuXLFuHr1qvHczOcs0Y6Ze50GDRqo6kG0Q1TiqYJOmOWfPGWykS59WlUGM/hImE3WtgwZMtjAeHVCf5jV18dnvzBbHcL4MZuv81Hmyy+/1NXUe9d6GI8vSbeJGxI8sfj222+taseOHTMaNKhv9blkyRI1e6zFPM7B/Bfnq9lmVMKsMz7rc9OiZQtDnzcc17YHk79uE68Q7gsWLLBmuDFj36RpE9UvzsH+/fthhkp4+pHScQQq6DF+fG9fevklA98RfKc3btxgVKla2WK0du0aZedPP/2kymJ8d1avluj8mO43Rq/eD1l1UIaC/n8nmC8kQAIkQAIkQAKRJTBl6hQlUuBecPLkSVtjIIS1mDtz5oxtGfdMXR4zyu6zx7///ruRI2d21SbEuZ3ryt333K2OV69+p2oaAlHPzGvh7d4nPkNkoW+U/fjjLcZDvXqqzxC+mOF3TxB4+gkCXFiQNm/epOqgHcz2e0u9+/Sy+oJrUVIJx7X94GmXcLOhZ4Ix6/3uu6ssO5YvX25XxXjjjTesMuvWrbXKBJs/GtZt4hU3eu7pt99+M8qWK6PK3dP6HutwMMYRqKDHzcWJEycsW/QbfI/1eDCLjwTRjzzcBHz99de6qPWKm1kIfV2Pgt5CwzckQAIkQAIkQAKRJABhAx/yl1952asZWuhAyBw+fNhrOdcDWvRA9NolPRtduUolu8PGE0+MVsIJLg5I2m2mfIVyST4lwCy1FpVwmYEg17bMmTvHti/46mPGW/vRwxccdSAGzUWQtnWQiWP6iQB8/pNKus3bsmYxMBPsLWHWe8SIx4158+cZHe/tqOyA77fr7LtrXeRr33BX9xE95mDxR5+6zdJlSnk9B2CMcriB0mskwAZ5KRlHoIIeTy68pYKFbld2ad/7xk0aq8+uNyPudV999VVVBuOhoHenw88kQAIkQAIkQAKOIgB3FPgTQ8y7+iD7K+hnPD3Ddlxa0Pfr39f2uLug1yIdi1g/3fppkn9t2raxBOSBAwcstxQtKuG6s3r1u17FOhYCoyxckJJLKIOyEIdJJX/a1O3oRb+PPjpcZ9m+4jhsgGuJTviMv2DxR7u6zYcfHqC78Xjdt3+fVW7b9m3qeDDGEaigHzt2jIeNOsN9Ma1e4Dtu3FhdxOMVC7I1Bwp6DzzMIAESIAESIAESiCQBuIRAqNWsWcNIyJXTwOJMLVxcX/0V9IsXL7Ydlr+C3tUGX99jlhgJLh/alcW1LtyMEO3kySefSORupMvAZzq55OpXnVRZf9rU7eg6L8x5QWfZvuK4LqsL6M/B4o92dZtJuTzBvUqX04JXf07JOAIV9P7U03b6Oz7NPKlXRrlJig6PkQAJkAAJkAAJpIgAIq+0btPaEmHw84b4bdjwLhWmD6Js6rSp1vFIC3q43MCVxpc/vTAWgOC3j1l5hMu8o1hRy59dizi8ovyff/5pjZWC/mYVgUh/wTQrfwWvrkdBr0nylQRIgARIgARIgASCSAD+2hBcmK1+ftbzicJE6m5S4kMfrBlixKaHnQj7GIyECDmwDf7diNiiRSdikyNsJz4jHGRyCTc+KIs6SSVtf3JtYuEu3J2QdFx+uB8llbTLDcrrpMcTLP5oV7eZlBsLXJx0ud17ditzgjGOpGba9aJm7QvvamtS9dxdbkqWKqFsx3oNb8nVpUg/gfBW1jWfM/SuNPieBEiABEiABEggqAS03zDCQHpLekEqhFqkZuh11Bv4ibvGi7ezGb7b2KDp0qVLxtZtW9WiX7jdeEuIaKJDd9avX8/QPvhYwKoXdtrVxTGUAZemzZraFbHyIORRDryTsh8RduDuhChAOrQi1jAklfQaB9xc6KRFdSgEPdylvCXM3qPvWzNnUk9FUA4LU5GXknHgyYpdwqZleqwpFfT6e44IQ97Csz7z7DNWfxT0dmeEeSRAAiRAAiRAAmEnoMXQtOnTbPv+/vvvrRCTKBspQb9s2TJLSE2aPMnWVmQiao/e6Ra7hSLsJezGLDHCKtolRLfB7rUoBzG/cuUKn/qCHZrf66+/bte0lffWW29ZZe1CPuqC+sYFT0xmPj9T1UFoT4TgtEvIx3HYgcg4Omm7QiHoccOhZ991f3j9+eeflTsT+nZ1dwIb5AUyDj2LXqJkcRVD3rU/vHddw5BSQY8xaW6zZs9y70rtYaCf3qAcBb0HImaQAAmQAAmQAAlEgoCeBUaUFmwO5Jr27ttrwGddixy8fvjhZtciXt/rOsESlAjPqN1b4OcPNxT32XPEqtfRZLDL55EjR1S8dG1L23Zt1eZCrkbDxQWLgXUZ3Diovv63OytEKGL1u8awx3vkaSGNGWv43ieVcFwvBEZsfuym6tom1jKMGjXSsgM74uK4FrSY2XcX9fisn7CgHDY/0kmPJ1j80a5uE68Qttt3bNfdqRspxPHHMey06hrHPSXjwIJl3S/4YR3EoUOHjLffflt9H/AkQN/ApVTQYzB4UoX+8B3D+cBGaNirYMOG/3j8X6Cgt04/35AACZAACZAACUSSwPvvv2cJU4gjiCbMUsPtAMIGrh/TZ0y3FpHCn96XpEVYMAUl4rdrUY/24SaDHUhhL2Kj6z4h5l03YkJoTH0Ms8uIbIM6EKBaDOI4NhjSsegRY75OndpWPZRr2aql+nOtgzKuO9YmxQblqt1Z1WozX/68yg6069ombjwgIpGw2Ze+SYGNiMsP2/Gqx4TjR48eTdS1PhZM/rpNfZMB0YuZc3zWUZEQIWnHzh2JbEnJOLCewPU8aBvwmj1HNrXDsLYnGIIeT3H0ngGufeE9npq4PpWhoPc4zcwgARIgARIgARKIFIH169cZlSpXtAQixAuEWd9+fYyzZ88qs+BCgUWDrqIpKXsxs4+/NWtW2xbr3qObOj5hwnjb41igi/oQr64JQhebYNWuXSuRvbAZAhl+0O5PGjDjjh1VIQyxC6irUMNNDNxc1q5d49qNeo+Z5RdfejGRCEddzMzjpmDRokWJZtk9GrDJQJvwM69arUoiO9AuxD7sdE8QtXgiod2CtP2FChc0nnpqgrWI1rVeKPjrfmH/xo0bjLp16yiRi3wsTMXiXLhoeUuBjANtgdmSJUtUNCaMC+cei7n1rsWInjNmzJMGnq7opMeP8+ctYSMulMPTENeE7wvCuGJTroqVKqgbFrzHkwE8SUFf+PPV/Qxtp8I/wkQCJEACJEACJEACISZw+fJlMeOIS5o0aaRo0aKSKlWqEPeYsubNhYty6tQp1Uj27NklISEhWZtNsSanT58WcyZeUqdOrcZ50003JWuI6c4iX331lSpXsGBByZgxY7J1kivgb5uQhKYLiJiuRpI5c2bJnz9/cl0E9bg5I6/ae+65mTJ40GD13gwHqliCh6/fl0iPI6hQfGyMgt5HUCxGAiRAAiRAAiRAAiQQOgJ2gj50vcVWyxT0sXU+ORoSIAESIAESIAESiEoCFPSBnzYK+sDZsSYJkAAJkAAJkAAJkECQCFDQBw6Sgj5wdqxJAiRAAiRAAiRAAiQQJAJmNBnV0ojHR0rXrl2D1Gp8NENBHx/nmaMkARIgARIgARIgARKIUQIU9DF6YjksEiABEiABEiABEiCB+CBAQR8f55mjJAESIAESIAESIAESiFECFPQxemI5LBIgARIgARIgARIggfggQEEfH+eZoyQBEiABEiABEiABEohRAhT0MXpiOSwSIAESIAESIIHIEli4cKEMeLi/jB07TsaZf+FOOgzkuHHjZeyYsT53r+tVrFhR9u7Z53O9lBS067Nzl06ydu1aeW/9e9KgwV0paT7m61LQx/wp5gBJgARIgARIgATCTWDf/n1Sp05tKV26tBLFN998c7hNEC2So1XQX758WcqULa24HTxwSPLkyRN2htHSIQV9tJwp2kkCJEACJEACJBAVBH7//XepdmdVOXnypHzyyadSq2atiNgdqKB/5tlnlL0JOROke/fuYbFd2+r+VEA/5WjWrLmsX7c+LLZEYycU9NF41mgzCZAACZAACZCAYwlMmjxJJk58Srp06SKvv7Y4YnZqkezvDH0kDNa2ugv6f/75Rz3pwBOPZUuXSYcOHSNhnuP7pKB3/CmigSRAAiRAAiRAAtFC4LvvvpM7ihWVGzduyGdHj0mJEiUiZroWya6C/ocffpAvz30padOklVKlSkm6dOkiZp9rx9pWd0GPMqtXvyv33nev5M2bV744+6VEwn3J1VZHvjeYSIAESIAESIAESIAEgkJg9OhRxi2pbzZatmrptb3z588bKFe7di0jW/asqjzqFC9RzOjeo5uxa/cu27p///238c477xiNGjey6qE+PiP/33//TVQPbeJv4qSJxs5dO4277mpg9YX8LLdlNvr172uYvuqJ6uXNl8fAX5OmTRLlt+/Q3sAf7J8zd46RK3eCaq9GjerG+++/Z5UNZHza1qrVqljt6DcYt3mTpPpavHixzuarCwFxec+3JEACJEACJEACJEACARL47bffjKzZbktSeG7a9IElxiFiby9YwChW/A4jc5ZbLbGdJm1q480330xkhTmzbpiLbK0yKO9er137dgbEr05aJNeqVdPImCmDgXZLlCyubiQy3ZrRagsiGrbrpOu5i2udP2zYUKuuzlu6dKmqHuj4dDvufWqbhg8fpvqsXKWSzuKrCwEKehcYfEsCJEACJEACJEACgRJ4991VltCFAHdPFy9etAQ/ZstPnz5tzaqbLjqGuQDUyJAxvWqjwO35LXGOmfeGjRqqfMyKL1q0yEB5pOvXrxtPPDHa6nfqtKlWt1ok4xU3A0eOHLGOYVb+gQe7WvUww6+TrucurnU+XqtUrWxs3LjB2L5juwGx/ccffxiBjg/96rbd+9Q2bdnykVXGXGyss/n6PwIU9PwqkAAJkAAJkAAJkEAQCAwc+IgSnSVLlbBtbcrUKep4+gzpDG+idMiQwZZwPXPmjGpn3bq1Vh5uGtwTBH/rNq1VGQh+PUuvRXL2HNmU2Hav9/PPP6tZe5SD7Trpeu7iWuenS5/WsLthCXR86Fe37d6ntunatWtWmXnz5+lsvv6PAAU9vwokQAIkQAIkQAIkEAQC8CWHMO14b0fb1iDQ4Urz8isv2x5H5ksvv2QJ18OHD6ty93e6X+WhfXc/ed3Qjp07jMGDBxmzZs8yINSRtEg2N2jSxTxeK1Qsr8p16ny/dUzXcxfXOr9FyxZWWdc3gY4Pbei23ft0bd+MSa/KPdSrp2s235sEGOXGkUuVaRQJkAAJkAAJkEC0EciTN7dcunRJhg0dJk8//d9Y7r6M4erVq3Lq9Ck5dOiQLH79ddmzd4+qtn/fASlfvryKmvPVV1/JkMFD5Nlnn/OlSVVGR45xjXLjXrlipQpy7Ngx6dixoyx9a1mieu4RZ3R7w4cNlxkznnZvyuvn5MaHirpt9z5dG211dyv54IONUq9uPfnww49cD8X9ewr6uP8KEAAJkAAJkAAJkEAwCGhROnbsOBln/nlLH3+8RZYvXy4HDx6Us1+cFXNGXRBv3T1pQa/bnTnzeRk0cJB7Ma+fdb1gC/qk2oMx/o4PdbStSQn6Tp07ycqVK9Tuu4cPHUE1pv8RoKDnV4EESIAESIAESIAEgkBAi1Jvgv7XX3+VLl27iBniUfWWKlUqyZEjh5QqWUrNxFevXkPFiB83bqw6Hm2CPtDxYbCaHQW9OvX+/0PHIxIgARIgARIgARIggZQTuC1rFuXjPWLE47aNIR++4lgU+/ys5w3TjcajnJ0PfUKunKoeotkklRBlxjVpv3TEofeWAvGh99ZeoOODbdrWpHzoTZcbVQ7x+5kSE+Ci2MQ8+IkESIAESIAESIAEAiJQqXJFJTjNXU1t6+fOk0sdx+JVb2nAgP6WuNWLYrFxFARv02ZNvVUzTD91A7HlEQcfC2+RtEj2JsBRJpiCPtDxudqalKAvW66MGlPPh3qgCpMLAQp6Fxh8SwIkQAIkQAIkQAKBEujdp5cSnN7CVmqBPW36NNsuvv/+eyNHzuyWENeC/pUFr6g8zOx/9tlntnVnPj/Tqnf8+HFVRvcXLkGv+/N3fDBW1/Um6P/880+rDMbKlJgABX1iHvxEAiRAAiRAAiRAAgERWLZsmSU67eK0YzMmCNeChW43zp07l6iPvfv2GuUrlLPqo9yHH25WZUzfdGsmHaEbd+3elagu4tRnuS2zqtula2frmBbJ4RL0gY4PBmtbvQl6c6GtVUbf6FgD5RuDgp5fAhIgARIgARIgARIIAgG4vWg/+iVLlni0aC6GtTZyujVzJqNBg/pGm7ZtjFKlSyqxitn56TOmG+YCUfUZ/vQ6HT16VN0IaOFbq1ZNVbdc+bKW0IUYvnLliq5i5YdL0KdkfHpc3gT96NGj1Hjg1sTkSYBRbvxfR8waJEACJEACJEACJGBLoE/f3vLaa69J8+YtZN3adR5l3ntvvYw1o9iYAt06li1bNmnbtq2MHDFKihQpIn379ZGtW7cKIr7o2PAojHjuU6dOkbeWviU//vijVT8hIUH69e0nI0eOkrRp01r5ppBX7+vXry/169W38l3fmDcNqq0ypUtLhw4d1SFdL3fu3NK3T1+ruOlvr94PGPCw9O/X38p3fRPo+Lz1ibbNzbTEdGOSL7/8UmbNmi2PPPyIa5d8bxKgoOfXgARIgARIgARIgASCRACi01y8KTdu3JBjnx2X4sWL27Z8+fJlMd1yJE2aNFK0aFFBCEtfkzk/KxcuXJBr165J5syZJV++fH7V97WflJRLyfjc+12zZrWYu+9Knjx55PMTJyVDhgzuReL+MwV93H8FCIAESIAESIAESCCYBIYPHyZz5s6RPr37yPz5Lwaz6bhs6667Gsi27dsUSzBl8iRAQe/JhDkkQAIkQAIkQAIkEDCBS5cuibl4Ve0Ae+TwUa+z9AF3EEcV4cLTtl1bqVy5suzYvlNuvvnmOBq970OloPedFUuSAAmQAAmQAAmQgE8EtJtIw4aNZOOGjT7VYaHEBH7//XepWKmCfPfdd7L1021SoUKFxAX4ySJAQW+h4BsSIAESIAESIAESCB6BoUOHyLz582TJ4jekU6dOwWs4TloaP36cTJ02VRa8slB69OgRJ6MObJgU9IFxYy0SIAESIAESIAESSJaAucmTpEuXTkWvSbYwCyQicOLECWvRcKID/OBBgILeAwkzSIAESIAESIAESIAESCB6CFDQR8+5oqUkQAIkQAIkQAIkQAIk4EGAgt4DCTNIgARIgARIgARIgARIIHoIUNBHz7mipSRAAiRAAiRAAiRAAiTgQYCC3gMJM0iABEiABEiABEiABEggeghQ0EfPuaKlJEACJEACJEACJEACJOBBgILeAwkzSIAESIAESIAESIAESCB6CFDQR8+5oqUkQAIkQAIkQAIkQAIk4EGAgt4DCTNIgARIgARIgARIgARIIHoIUNBHz7mipSRAAiRAAiRAAiRAAiTgQYCC3gMJM0iABEiABEiABEiABEggeghQ0EfPuaKlJEACJEACJEACJEACJOBBgILeAwkzSIAESIAESIAESIAESCB6CFDQR8+5oqUkQAIkQAIkQAIkQAIk4EGAgt4DCTNIgARIgARIgARIgARIIHoIUNBHz7mipSRAAiRAAiRAAiRAAiTgQYCC3gMJM0iABEiABEiABEiABEggeghQ0EfPuaKlJEACJEACJEACJEACJOBBgILeAwkzSIAESIAESIAESIAESCB6CFDQR8+5oqUkQAIkQAIkQAIkQAIk4EGAgt4DCTNIgARIgARIgARIgARIIHoI/D8FrRy/Q7WhYwAAAABJRU5ErkJggg== />"
Question 3A student proposed the synthesis shown in Equation PE 14.5.

After extraction and recrystallization, a white, flaky, crystalline product was obtained that had a melting point of 117119C. The desired product, shown in Equation PE14.5, has a melting point of 152154C. Write the structure of the compound that the student isolated and briefly explain what happened. Write a rational arrow-pushing mechanism for the formation of this product. Hint: If you were actually doing this reaction, you would have prepared a prelab writeup that included all of the physical constants for your starting materials.
Question 4Propose three different syntheses of the alcohol shown below starting with a ketone and a Grignard reagent. In all cases, first show how you would make the Grignard reagent.
 Question 5
Question 5ecmC4w4AfLpTEBHAiwwdITJWTEBIwmQEHjhhRfwyG5dsffJJ+GaNa64iyPTq3POPUeaYpFJllYoXKXcbkcdiSf1tqDL9U7c5XIGzSNQ4fTNImgIC+GZJwWA3alEeapCh4wwZUGx6F3zCgpztFsJVSvKsueXYI0qW091GTp8plFUl8IK1Zdh8uPdAQIsMAIs4t3SEhg0y/re++/Fm7Vu55NpKb3D1emll1ZIc1P1Pt5mAqlOgAVGqt9Brn/GEaCZhDmOOXIm4eLRF+OWLVuazYBMrXJypkvTKzLB+umnnzTzcLvdOHjwIOx0UEd87PHHdJ050SyQd5qUQC0WZnuFjCJobHY72qxeB3BlX25xU47gJr28JFaLBYZ+8LUEBr0ryZyTzDrJvDPZid7fJSVvBFWDBUYQDv6QJgRYYKTJjeTLyDwC3377LY6fME42nnfccXtUvhBkWkVCgUytSDiQgNBKat+P6dOn4W+//aZ1GO/LKAINWOFyol01W6EIC1t2HpZWxm+OlVE4fRfLAkO/u64lMCj3yspKadZJ5p0kOKiTb6bEAsNMd4ProhcBXgdDtJCcmEAqExDT/3DjjTPgxx9/hPnzFoDdbof/+7//07yk2bNnwfLC5ZB370IYPXo07LXXXkHHiVC08PAjD8PcufdA//4D4IFFD8Dxxx8fdAx/YAK7dmyH2voGAaIlZHXoBFmtmEmsBHgdjFjJBZ/3bum7MHLkCOjTpw+8/tob0K5du+ADxKe1a9fAjTfdCL///jvcuyAPxo4d2+gd2Ogkg3eIwRu4fNJlsHHjRvj+ux8MLo2zZwIJJKCXUuF8mAATSB4BChH7zDPP4CFdOuOAAf3xg7IPNCvzxx9/IK3KHZrIz4LW3KC1N4497hh89dVVmo7eoefx58wisGfPHnzyySeDno1ffvkFX375pcwCoePV8gxGfDC3bduGl1x6Ce63fxsUi31KX4bOhxyMTz31FNLzGppoFpcCZdAsLgXOoAAayUi0rpAYzMGOnQ5Eq/VMfPfdd5NRDS6TCRhGgE2kDEPLGTOBxBMgATFz5q3SbOqyyyfiDz/80GQlvvjiCxwxcoR09L5/0f2ajt5NZsIHZAQBMp2jDrE6GABFICPnf06xEWCBERu3uro6FDOyUlhcOu4SrKqqkhnRYEthYSEefsRh2O+Uvli6vlSzAPJDo9Dfrdu0wiuvmhLWD03z5Dh3vv32W9jLciJ273GUFOc0wMOJCaQbARYY6XZH+XqYgCDw9ddf46gLR2FW2/1x7ry5+NdffzXiQn4V5OhNC+qRozd1HjkxgUgEWGBEohPbdywwmseNBMSyZcuaFBDhBEhoaRUVFXjueefKAZa8hXlB4jn02Hg/03vZNsqGbdtl4fwF8zVnk+Mtg89nAmYhwALDLHeC68EEDCCwevXbcqTsqO7dsKioSJq2KI7eFBkqkqO3AdXhLFOcAAsM/W8gC4zomZLp52mn/Uuagj799NOaJlChualNqO6++y7cuXNn6CHy8xtvvI7Hn9BTrgW0cuUrQWaAmic0Y6d6ZnnS5Muxurq6GWfzoUwgNQmwwEjN+8a1ZgJREyBB8cijj0hbXzIZoAX1KA47ranBU/NRY+QDBQEWGPo/BiwwmmZKpp5k8knhZm+7bSZSh725ad2767BP35PxiK6H43PPPaf57vv777/xwYcexA4HtkeKSFVerqwt09zSvMeTDwgJIfKNI2FUtsG3GGZs2fFZTCClCHAUqQQ61HNRTCCZBGS0kssvgw4dOkBBwRJo06ZNMqvDZacgAeHQDYcdfijsrPsT9t13X3kFYuQXbr/jdvjs040peEXJrzJHkQp/D0RACnjgwQcgL+9eGDbsLFiYtxB69OgR/oQmvhHmVeB0OmHW7Dvh6B5Hw6IHHoBT+p3S6Kzt27eDmO0A51InXDH5CrE9Bzp27NjouEg7lOh+QpTDgvn3wrhx48JG94uUD3/HBFKWQErJIa4sE2ACTIAJJI0Az2Dojz7RMxiecqdc+d1CK8Bb87Am3CXVV2COb5V4S04xNo49F+7EkP2eSnTm2mWZoqMU+GuxYV5RGXpCDqePNLNKJp1k2mk5qReSqaeeaceOHXjzzTdJB+8rpkxGEeJbM3sROhaHDhuKB3bsgPmL85EiPzWVaH2iceMvlc7ns2bdieQLwokJZCIBNpHKxLvO18wEmAATiIEAC4wYoDVxSuIFRkGgky86/EWV2tKhtiwvcJy1AGNZRtFTXoTWIFFhRZvNGsiXvrM4sLIhAIkWxTvzzMFIPmKPPvYokomnUWnz5s143vnnYbsD2mI4B28SO6+88jIefUwPpCh74RL5dpCPBy3mN2bsGNy6dWu4Q3k/E8gIAiwwMuI280UyASbABOInwAIjfoahOSRbYNgK3KFVEp8bsDjHEhACtgLNmQaNEwO7aktV4sKOxeXVIldfaqjFskJHIP/sIv8Micv1jpxdoCh3iUolJW9IB28SEeEcvCl6lZbYIQHyn//8B7seeQSe3Kc3rlu3NlHV5nKYgKkJsA9Gyhq3ccWZABNgAoklwD4Y+vNOtA9G3aYl0NZydeBCLA6o3jgLugT2AOz6BCa27gvLlX22AvCsnApZymfxd8eWTbDhi22wW2zv374bnPKvXpDVInDA+oVDYNDMtWJHDlTUPwjHaaz2/uOae+DQobPlSQXlHpjaS11CIK9EbAnxAI89/hg4HHPEauB94YFFD0CvXr0iFi0W6YMbZ8yAr7/5Gu65Z67019h7770jnsNfMoGMIWBq+cOVYwJMgAkwAdMQ4BkM/W9F0mYwbNlot3p9IgpDzKRqXN7ZBbsjD+1kxhQ0g1GDhbkhZk7SDErMUlT6PCrq3d7zxH6HK6yXh4BZ758psTq0F8TTn3jkHGtqavDaa6+R6wNdf/11+OuvvzY64aeffsIpV14hfThuuulGJJ8OTkyACQQTYBOpYB78iQkwASbABMIQYIERBkwcu5MmMLKdWOLMlmZKtny1mVQ9FmWT8LAKs6ZSzA4SGA1Y4jedsqDDWYxlpSXosHmFCoANy0hjeNxok6LDhm5tFw8/saqiHK+plDU/Jj8Pf0Y6b3z22Wc4ZOgQGd578cOLpYM3rWC/8L6F0meDfDdokT5OTIAJaBP4fwAAAP//8qKw5wAAP09JREFU7Z0LfFTF+f4fKkGiBgsYingBDVbAsii0Bi+oG9SCWpdaUEsWJV4C3kJABYOCGlQM91BtA15CJaGtQSXYGrRN6D/YGn4ahEQJSsCgBmuiiSZoIkk7/5mzl+yScza7ye5md/Oczyfu2TlzZt75zsqZ58y870DwIAESIAESIAEvCPznP/8RvaOOE83Nzc7cf/vbX8WY803O7zzxjYDiqf6CdTSUZQkAApZcUVOdbzs3pYtqhwENJcKirpuzRF1ThbBqebNEg7zeUmXPD7MoqGpx3CE/G0Ruskkry5pdIZrKsm3lwipKm1yy6Zw681psdehk6bak//3vf+LVV18RccPP1v6GDjtTjDpvpHjjjb91m02smATChUAvZaj8x4YHCZAACZAACXgk8OWXX+L0M07DkcbvcPzxx2t55WALCx9eiN3v7/F4Ly/qE4jq01u70HK0VT+Dn1Mby9ehn2k2YM5GU5EFa8cMwIIyILeyCdPj+uLwtoU4bfJSWHMrsXH695jSy4R8SxYatswCHPfCisKKxzCk5Xu0SPuiTjgBVZtuwOTFsiBLNmpWnoRBw6fJK6mobFmNOFsTdVvitMdeR4xuru5NlIIa9953j/zN98Wa1WsQFRXVvQaxdhIIAwIUGGHQSTSRBEiABEKBAAWG/3uh+wRGlhQYs7B/3QyYZufAklmKLSkmbJoRhcQcEwqq92DSgF2YET0OOfbBf9UGmTcpxzMEUybq3