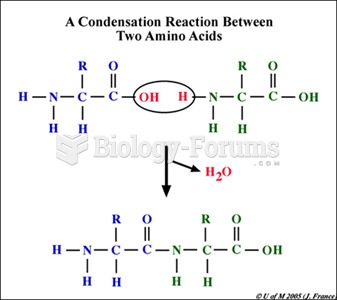
Which of the following is the product of the first step of the reaction catalyzed by pyruvate dehydrogenase?
 Question 2
Question 29OeLvPUMa9uBHnFdKPF9S5m3AvABAUp9Xip94uYtdGTpR3pY8gtrcy2uRmA/CBimqRb37B3NzGXDtNPo9cfle78Lh0z+eBfTJ+zzdaNfSBdjGE7K5m6h4B9fEze6K4RCVCzdSsqfxhB7bDdM06cnrhuNaPRGjGg34rJd5K/ktQ3L2VFZSq+EFC7uMRyP3c3Kgq2UBQOMTu2myCenqoTvCnZwasdeio+ahIj0OqPo/ZJoyX6VCDSgrZhmAAAgAElEQVRIRvUh0lyLXmWBq1oEmV1J6byNynMu/qTe0N5NCH/1gtgm6Yjqq5gOaxEEImQkrGItZpUFruKwEgAqMc2g9T2Qb4DpVTJZ8VyEzKrqAckhfw80GbVIe+tCNAKNRWC/c0aNzehQ4qmOxZDOx+SnqmyY1JPQpJ78VLlNjYxtqgezFjweSjk67eFHIEIiqjVN8Yzz8d6mheyqyFPCWeF+MMVEF44t8cwqZaaVkEgeh782WgKNgEagqRBoAjLazLSxGRjXzz8kmQxTdl+IY+Y7M9myagObf8ji4/dmAeLSrTugQwI3yhLXJhM7S3ZtpVDNCdV+YxFP7bAoq4oWRyOgEWgiBBp2YKinkAnP7arj1dSdKYt2MaWeuAceZOB2e3DYHQSNIDFuWfSor9aNgEmMy4lN7UfYumuqa6cR0AjsG4Em0Iz2nfmhvdkzu3Bo+ejU0Y6A7DmnL42ARuDXjUDUkZFQkEVDuoP69Xw1pcV1e/962lvXVCOwNwJRR0Z7i6hDNAIaAY2ARqC1I6DJqLW3sK6fRkAjoBH4BSAQPWSkDjQSF15BLXyonmWv+wXAqEXUCGgENAIagUNBIHrISI56xYbP5yUUMgmFAupezyUcSvPqtBoBjYBG4JeBwAG7djdPtawJbNMs48KLz6Nzl87KjSEtXY6GLm+eIlsyV3VarVbzWhJyXZZGQCPwy0IgSshIQJPtYVzExLh44rGpVFX5OeOMU2nfoUt4qxgrzi9HUwqTj2FXGh/4o9JjLEKREV82a1jQ8l/iSPktX7IuUSOgEYgGBKLETGeA4SHrpywuOv9KAgGT1NR2XH3VDbz3zntgJIax+gV0WWruK9ylG26yftrM449MAyMmqo5Pj5CQACuo1nxu6S+moc6HOJwStHSNdXkaAY1AXQSiSDOKYdq0aZx2+qnc8ud7lJyjRg2moHA3UKVO/MQULSPKOy0192WCIbtHJBIyg6xbl6XulXZklIEpm4IePmKNiIghO8HJRqV+a4PSwyKVgcNux2V31v1u6meNgEbgV4RAdJCRbJIaKmfz5myuvvpyoBTMCoYMG6GawjTLsY6cjnIiqv7ixPDdim9Ys3YzOTt3krsrn//+5xWCIS8nnngsqWmpYIYPEKxO03I3ShMx3ATw8/HP3zI8rQudPRkKc1N2T1d7pjctXUZarhYFGx58po8VhTsYWJhN14QMMLxg7jFpSrpaaVoOJl2SRkAj0IIIHD4yEnOWDNGVBmHHNCuRzZntjpoiSYet9nEGI946bE0dKxDl3ZNhJycnh5U/rqa0rIyS0gpWr/6JYLCKsWNHheeQWlY7sshA5uVEA3Hy+c41vLP5WzzOeD7etpaR6V25MvMoHNIeZqX6CjYVEUSISDJVZCcmSxzMyl7J+5u/4+iMPizM2ciKvC1c1288nWPTgApCdY7aivJWb8GfrS5KI9D6EDjg84yaBgIxY8kZNrEsXfI5ZaWlnHjyOVx+6QWcesopXHbF9co0tytnCyXFxWT26sv//vce/fr2oU+/kUBJrdFz08jUlLlI/TzKNLchazl/f/wZ/jn9JWUOg+Kwma6lp+tsSqaNpTt5bu0CvMEAv+07lsFJmRT4CpixbgEbi3ZzUeYRnNihn3IasQ40bBoKUMSmnDliWFW0nRfWLcRm2Lm23xj6Jor3ZECR48c//8hR6T24ss9o3DanOjqiqUixVgvr84xqwaEfNAKHGwH7PffcY03Q7CVJc7hUSydtB6MtOTk7mfbkU6xYvoLx48eTntGONolxPPTQ43TuksGO7Bxu+N0UOnXqxMDBI8jPz+elF15lY9Y6+g8YTExMW8uko+aQmqbD3AuCgwqI6AFBMIJkb9/Gyh9XceqEYwCZL5L3LUxERiylQR//XP2F6vAndBrAlIEnkuFJQEygsQ4H4zIG0qNNMm9tXMZn2WvplphGqjtF1eGQ5+lkbsqIpcBXwVOr5zH759Wc3X0Yv+t3HKkxbkyzAoMg/ZO6cFyn3nyTu4WX1i9Rc0m923TAUDt6W1ryQTVJfYmMuPpCdZhGQCNwmBBoQDPaZREHYh6TORw5CE2sZuLZVhk+/Ky2Q4Gp3LPFBCM/dIkvHa90wNIxC2Ek4PdX8Pqrb7L8m+WccuopnHHW6eEdF8RJoQ2ffjKTd/77nuqIJkw8hTPPPssyGxkJBANVvPXGf1m8eDEnnnQC55x3jjWjYFaEZxZC4QmGGuQk1kB5q7zcpAJCBEFlIjT3Ozsi5GnlJRxSI1cLi0b89/sDVFZWkZiYUMf5QklVbw7yRi5loDRsyrnAepZAwVx2qJC6ikRi1pQwcUIIYRomUlUlqzKH2Xhvy3d8uDWscfQ+Co89RmG6p5zwndJWHXyavYq3N62gb9t2TO47hjbOxPB8kpWvsq5GEluiqv+RsiWWvFb/DTfyvXhjwzfMyV7Nse17c3mvUTgMR7U5MCxtuJ2kfdxklexgxrqF+EJ+JvcZz4Ckrup7FyKEHLZofddqmnQFXsEl3GaRxjIlZqSEGsJqzagGGPpWI3D4EWiAjPIpKyvjww9nc845p+OJ9YBp4713P2DYsMF079EzbHaK/NSlE4gje/sWnp/+MoWFRYw8ajiXXHaBMsdgOJk393M+eP9D+vfvy2+umkRcXBKW2UqIS+aPBBAhv0hPIs9ChPIp+UtH1ZbcXT/z0ksvk7crn0suvYQRRw4Hs0SZ/taVGXy726RtjMHJGSEcRqTjdrK0wMZPpX6GtXUwuI2JaQYiM1L7aAk7q0qho9skyXmQI3NFGPawaW4fxdQTLFX2hUKUeL2kuj2KTEWCgqoKEpwe3A4xc8J3hdsp9lcxPLkjiY5YzJAPwyadtIdv8jfxyk+LaBPjZnK/8XSJy1BzMdbAoibGdQQw3HhDPl5dv5QluRs5ufMALuouziSSxmf193WSWN+CyP/I3JSLhbt+4vUNS2kXm8R1/cbRTrQtNXhQjVonlxqPkbmtHat5feNyerRJY3LfsaS62oQHQybFfh853jICoRBxDifd4sQxJKRIOYCJzbBIy17j+1Rda01GNcDWtxqBw4/AvsmIInZmb+OC86/ifx++QUqa7IZg48yJ53LDjddyysQzwCwLj/aFSFzs2pnLpEuu4ZRTT2DAoGE8NXUqo8ccwR1338ujDz9CRXkJV11zJd179A/P+9SdxBfCkU7KFiagegASckEm4dvw4/df88rLr9Krdy+u+921vLbZxz/W+xia5GRTeQjphN4e5yDRafLXH4N8mROifxsbS/MDXNbDzu39hCREa5Nywt1UpI80TDZVuBgws4zbB7i5e6D0bAdJSPVUo6Eg1aUbLpYVbOFv33zCuydfQ4xhUBkMcN68F3j8qHPVJP/1S99Qpq84Wwyby/KZOvJsxmf0ZVtFAS+sW0ROZQmTeh3FuPRegFeRr1XPiL9c/VJY5QsesWRX5DFj7QJyq8q5svdojkrLDDuSSNvtuVQaeVTkG8uWsl1MX7eAcp+XK/qOYURy92oZwi4pexLXexfOUbz+zAAvb1jGgp3rObVjX87uNhSPPZa/fPsuM7etoX9Ce3J8xfROTOXZ0ZOYuXk5ed5KcquKmdxvDBnueHWkfTURKTnl+6wvjYBGIFoQqGPnqC2WYTNIaptCUnKy0kjkbUpKKg6HkIGYifaYiGQk/urLrzJwUF9uuV2moQKMHjOQVSvXYIZKOPe8CfTuM9DaTcEsCHf+tboHK0wtgpGSpDOSq04cM2xmYzeDhw7l8aEDyFq3Bn/Iz4NrfEwblcBJKT5lvrr9uyrK/DZWltj433aTBSd7SHEEWVFk561NPvwhG06bnU1lBkVek6EpNmyGmLuku7Tz2sYqTunsZnFekNJADAmOYL1aQVjQJvyQupv4TZP8oJcYZT4zibEb5IV8eJwuXtm8mN2+Sj454VYVd+raj/g272dGpvbkn6vmMSi1E/cMnxAmdjFjirYiViwxTu77ipCKFa+MjrEJ3DviPKVl/Xv9EmZuXcnk/uPpEvZ4E0AiaTBiqQhW8uK6z1ixeytndRvM2V2Gh82K5SLBfjTRsFxqwGFYWJuVOAyDa3qNZWLngTyzah72kMmFvY4nu6qUq/uN4/96T8BHKcP/9xCf7lxJrq8cl9ODw+skNUa0b2/jyt03LPqNRkAj0MwISM++j8vE6XBSUlLCX/78Nx6456/cf/ft/LQ2C7db5oViKS8rY93a1eF5GAerV61n9JgjrUWq5m7aJiUz7ujjsNvt9O7Tt8ZcU0PdYUQcidNQPOlZxckiQK++/bEbJkPa2rnvhwr+vcVgS3mIh4fF0iHWxgfbghyX4SDFIUTjZ0TbII8Nd+K0GUxbF+T277y8vCnEpEVecqpcGIQoDtj5YleIp0e4SXCEeC9bNDLRtULVNBmRtKk/Lc3BwIkNLwFWFGWzpjiH5YU7CYbUbAmdY5PZUJLLvzfOZ1PZZm7udxJTBp6MAy/3HnEal/YYZXkcKld4kVDw2j8ZRBC3PsPaoFnOkamdeWbMRQxN6cxdy2fyzLr5VIVEk3Vb7uJGDO/9/B03LvyPct9+euzFnN1lhPKGw5TBgVWrRmElAw4la0Ru4dIK2rs93H/E2ZzdfbDSzsTbbkdFEVkl21mWv5XuccmkuuIZndqN0amdubDHMOxSkci4plGF60gHhsBsrlMOKuKkUuPvutkHlk2t2BuYNlbyuo76cpl9nYExdhobaqWJ3ocN08ZWYzN2Wj1Sz76OPXBZeO55jt56NbVkDWpGMjq2O2xkZnajTaK1Jc+XXyzE7fHww/dLuO/eB2jfvhMul8F9DzyAwykT6RF+i/QA0huIw0DkuYmroBwrfNgweX2sg0fXBHl5o4/H1oQYlxrk6SNiKA8ESHRL+TI2j6xvCrCqxMlLm4J8epKHDKfJNcvgiXU+Hhvq5L1tJsmxMXSKgeM7xfLmVi9XdJV5GjHVSV6RbruJ61MjO6fdQU5VCfd8Nwu3YafCDJDrLcEb8HFmpyOpDPh4bt1Cpq6ZR3t3Io8deS4D22ZgV84MVU0roSIUOL/7CE7u3I9/rVvE7xe9zcU9R5LmSeDFdQuJdbq4c/ipdE9or+amxEvugEioRt33vg0TIyFc4bVoLqeTD7b8wM6CQhYVbuSiHiMYlSpmxKo9XothItw7Px3SJAhsWM8qxjA1axFTBPomvWYw8bqzMaeLhv9LvWbz2M2LGTM1i0X1AjSb6ybOgFnTf6kVbDK5GyAjk0AgSGxsLFddMwmHM0VpBrNmz8XnraK4uJTf3ziZ4084m8svPZfl3yxi6NAhfL1kGRde8lswUsnP28jatesZf/ToPd54TSZ6zYxMfCEbK4uC3N7fpv5y/U7Gzylj7i4X/RINlhaKZuMIuyoblPidbCgzSXcbiojElDMyzcW87V7lzfWfn6vYUhbkki+97A7CkgI768oN+sbJqF3yav6rKugnMzaF/x53NW5slJt+TprzT7ymn7yqXM7tMoiLuo2kwFfGHT98zP8tf585J94QdixpevlUrc1KEh12/m/gKawv3cHz6xZS4qtiUq+RjE8X7VfmpkRjFa0pTNtNOg6JuEeaVPq9XNN3HH/pexqrSjfy2wWvs6t/PhkxCZjKcSXYtITc9JD+8nPMWsNiBnJHkxMRMGYMY2bcz7RbJzQD0bUs9AN7NwdALVuH5i4tosbUU47Y7EMUFRVTXFRqebVRQmFBkSKi4088izFjjuTOv/4Rt9vNEUeO4vwLz2X58u+Z+sQDfDRzJpdddh1fL/s27CFXTxFNFST+EzYb1y718vA6G+VBG4VVJi5sxDtMzuzk4Otdfj7dZackEMODa2HKsjIGt3WR5zWVx1yQOObuCDA2w8G3RSa5FUHePjqWO4e5+OdID6d2sDNtXVXYjboB2JqgTtYsjDW/UxUMYFdaZRBbKIQvGCTBGcf7P3/PSXOfw2sGSHa1pZ07gRjl9m0J0Bx6m9Ra1Vy5UJfROyGVx448m+ljL2R8ek/LbKo8FEUGyywobtjNdcnCXTMojhQ+BiakYxo21pXmqzayjJnNWHhzVeoXlu+G9atg8tk0i+4y8A5engo3P1afsa4OULOvqzaFibmwtjksYvqqbVKsawqraU7bO4865dV83FfZG6Yx1pjIDGDGxHrMjnXf1zQ9rpe0e8yeByyryntPeqnPAedRs44tcN9ArxoiITGeG278LbFxLsuTzPRz5dUX0advD2Wucjqd9B84EIfDxZbNm8lo35V/v/ocefl5zP9sFjfc8FtuueWPYAqZNeNlGjiNEI8fGcvHO7yc+5Wf3y+r4vpeTo5OC9I11s+jw2K5f1UZ5y308U1+kP8bkEiPWB9/7u/i3h+8XL+0gk4ek9/1cvHlzkqu7uFgcEKQ/okhMuND3NLPTklliKqgOAKIqa75rsjsisfmoLtHXJlFJ5GO1aSLJ4FA0M8F3UaSFOPhzLn/5Oz5/2B57mYePeLMsINIhM6aT0aLbPzheSlxn5d5oT2XkGFzEKKUYFGMSYeYOFKcsiGt4GNnSJt27CgtVJRpKEeY5pJgTz1/7XdZaxYzZtX9DRDBoSGUOeUOJs+YuFdHWitXIYOJM5g8S5ZryN8sBt7cC6NO7ztj4v30z7LiZE0dw4yJY4lM4QgR9boZpobfm1nCgr3qkFqtUq2HhsrOnMIicxaTISzb9NqkXff9oilE9KcZN7/NhQcrqxBRr5sZWI2HiTlrsiLECCQHXd96IGiyIHNfVyjHNM1c0zQrrU95VmHlpmlWmW+/+Zw559N3VOrrfnu5+a8Zf1fhpllkmqbPNE2vaZoVNdLuMs1Q8/2FwvL6zXxze2W+WRbMM00zT5UZCu00TTPfrAzlm9kVu03TlL8cMxTcpeQr8uea2yrkXsJ3mZWBcFpzZzi9yJ1r+oK7TX9QwgSL5quL5B0K7TIDgRyz1JdtBsPP8lnmyzZ9AWkbkbXAXFO0xlxTtMqqq1lghqRe4fjNLePhzr/cn21W+ndU17fcv8Ms9W43Q6Hc/bfPvr73OvwAEJhlTpaxwZipZlaNVLMmY46ZWjOkxstG3WaZU8dgSg8uV9bUMbXKkPz3lGnF3au8WZNNGGNaYlhy1oqTNdUcA6ZVRD3vpWCVx2TTkqI+wRtfdrgq9WRilb3nfT2yHKis+5W7njIaVd96xG/CoAY0IxmCyhhU9lKz7P/WaFjWFvnp1Lkr0599gd9NvoK4uBjOOe9sazGjKZPHhWAWWRqRyqMlRqiWWdFhBunoDhJnE6eJoFqpL8YlWeDqNgJ08ATUaN4Sy0rTxhGik0fMSgFVVbdKK4snLXgs6UM4bT7shj08Mm+y8cA+M7LbDOKdYmyUy3LJjnO6lBeg1Ec8Cfu1yaBfm/aqjWQvObX5bDNqJfsUtoVfyDcz1uHCbd8z7RnrcBLvEk/PiO7UwkL96oqbwHTRRGqM6AWCCWdPZvHNj9XrCXcwEGVOeZmp3MwVETWmZiYbPubtxbDXnEyv/oxhMWvk9JbwVStOZm9koYm6Zn/ADMZw4WkRvSQcrvKYwQf7shIeQNnhHBv9cUiyTjibycxg4j68ETnY+jZa+oOLuOeXvFf6MIFE1v1EPiWeWcbosWN4bfggcnPz6NK1W3gtieXCu1dWLRBgSRuRWQqsFRKew4gIEjGESacVnmUPd2A1U4VzCyey5kAiG91Ecmquz+qyw84SEYkjzhPqvWLUPYtPq+M0l1BRlK9Vf8uRZG+sLEGrw6NI7l+FKKoTv5kPZk9nQpNMJmUy5Y7J3DzxMWZPaaTXWU2yaRToi7m5l8HN9cStJq163tUbdMBl15tLA4H7k1UGCVn0H9uLiYbMWFmXmDH3OCbuL49Iqpb7bFgz2qcc0jFX4va46dJV9gyTEbl0ivrnv0/I9AuNwK8KgTH0l40/muqaMJ1Zk2dwf33aUX1lKJfz+l7sK0zc0yNzTrU/93Tg+0pbJ/yAy66Tfr+PjZE1kymL9tRj1mRxotgzR4Zyx9/z3pprs54PuL77lbdxEQ6ejJRGIaYwmcSOFKbJKIKE/tQItHoEwh5bkUnx6vqG3b2b2pt5wq3iVHAF96+qLgkyT+PCMbBqfZ3FpEqGRhKiMmvVNunVKGHft01R9r5zr//NQco6Ybo4UoTreJB51C9Q04UeJBlVs08dSfYVXieaftQIaAR++QhkTuEOGXHXmVSZ/cEMxky9tbbnWFPUVpW3mMWLa2ZmmfAW39yrhsddeCHp5DsauT5pArfW8a6TEtROD0ZNbaJmuXLfFGVbee5FpnWLqn5uhKzK1byO3OF5IktbbUQe1eW13E0Dc0YNCaE1oIbQ0e80Ar8WBCZMN5kl2/PU6BJkbmJR9VyRbO3Ti5sHzmqSnRTUCH+GtXanGuMJ0zFngTHRUGt6JFx2PDDr3fGgOlWtm8wpi8hiLL1qzRtNZpZZxx27Virx1jjUsidwthC6uKK/PZWsRb3rlrDX835lzRSZrsOoVZfau2TsN4+9Sm3+gH3v2m3mNn/pugSNwOFCQB8hcbiQ1+VqBOpF4CDNdPXmpQM1AhoBjYBGQCNwUAhoMjoo2HQijYBGQCOgEWhKBDQZNSWaOi+NgEZAI6AROCgENBkdFGwtlagh78SG3jVGvrrp6z7Xl0dj4tSXTodpBDQCGoGGEWgaMlJHhTdBR6VO+GxY4KZ9W8MFSGVc97lpSzvw3EQe+RNs6+J7qLLWTV/3uT5pZXv0unLUF0+HaQQ0AhqBA0PgIF276xQiWwWp4wvkAD7Z0Vr2s5M4jengauQV3guuRoh1q0hKeLOtOi9HTv2svlTnGA/InmRySfkl4X319lW+7LUXq06rhVJQp6FKXNleZl9pwtm3yIeAF5bD8ISPrZCCRb5Kawd1hbfUQc5fknC5r7DeHYiMKn85I0iOx5CrRtnhkNofsWHRpA2kveX8IjnIr2nGNbXLqvkkx9zL4YZSz7JwPQUjaUsJl927pS33J3/NPPW9RkAjEC0I2O+555576hdGDkhr5GU4KC4sZuq0qWzespEhgweDIpDGduzSoSSA4UA2+5SzN2pdhoHfH+TZZ/6J31tFl249w6QjJBjPj9+v4MH7H+KDd98lGKyib79+4eSKEWtlZXVecSxbspjnnn2G1JQkdfSF2tIoQgB1UrT8o1V/2aJj+bIVrPrxB35at5qSkgLad2iPYcRSVVnGnE8/w2aYxLgdLPhiASkpbXG748LktB+phcQNO98sW8Hu/DwyMjIaQcZ2vv/ue3bu3EFaagqfzJ5DKBQgJbUdhhoE7KfMQ3rtZMeOnXw+73My2qWG6ynt6yRn506+Xvo17Ttk4HQIMdXX7nUKNwQnfWkENALRgkATDWfjmTNnPn/5ywP89da/sSN7pxrByuF8GE4wksBIVJ2fKaN4FZYMRhtLozKS+WzOLJ59+jkMm4TL6DshPOoVEVNU//Lwg39n3rwF4dGxKA+xfLt8GSedeC67dxeRlJzCJRdcxX13PxzOQ8qWMtqCEd7NWWkUBo8+/BT3PzSNp6Y9rzo0a9VeHRI8nK2kDtay86c/3s3VV/2Bhx58movOv5qTjz+fbT9vJxAwufeuh1iy+Bu2bsnm7DMuZcOGrWAIfnL8u5CN28Ja3dvCz/IpmIo2mcBfbruHRx56Ktw+MZaWIZqGaBiSj3Taoj3JAMHwcP99j3PvXY/g98F99zzM5/O+xFADCUkreEt8q3x1qlJ1HvI+DKgiQpEtXqVR1CEySRsZchqv5CF5SZlyL+FuVq1cw+2338327TvDckp4MosXfcN551xBXm7BHvnDeTeKmA5nO+uyNQIaAYXAoZvplBbj56033+eqSZewevU6Zn88h2sm/x7DFmL37nxef/U50tNTOe/8M3G6EtiVs503Xn+atIwUJk26hKWLv+LWP91DKBSkX//+xMTY8XorOfb44ygvK2bunNkMGz6YtPR2eGLFbBW57Dz99PMkpSTz2ptCKm2RA/+2bN2qjleoKK/krTdepbikiPPOP4suXeVQQMhav4o1P/3En27+PbNmzyM/bzOpaaIZ+CMZR8Gn1XMHAj7OOus0npn+HD+t/Y4Jp5zP7bf9hdffeplXXp9ORrv2bMhaT5s2bSkrq2Dpkvn07dOVtsmpbNywnsQ28aSmpimNcuvWjXTr1hmnK55lXy8hJSWNxLZxxMa6KS8vpqQ4B5crhsKCYjJ798XvL2fxws9ISkpi8NDh6tA6d4ybilAlnrg4/v3q06SmplNY8DNVVRUEg0G2bN7G2HFHYticyC7iXm8Vixd9QVp6GgMHSh5iDnSwdfMm1q3LYsQRQ0hN60B52W4KdhcS43az/qcNDB8xhNi4WBYt/IJevbqTntGFUaNH8M47/6Z7jy5qAJG9fT3Z2UWKNxMT48O7AMSxI3sda9esY+RRR5CQmGQdbdLsZsQo+MpoETQCv2AEDp2MiGHrlp9Y/s33fPHVRzw//RXeefdjrpl8PWXl5Vx4wVWqU9mUtZEFX3zFfQ89wPnnXsqIEUcx65P5LF/+A6NGHonXH8Q0/axfn0V5WRmPPPwE23PWM3/eV1x/3RS+XjYfm92uZkcU3oYNM1TG2rUbOHLEsPCcUS73PXi36jRLSws4/5zLsNkMOnbsyPPTz+e/777KgEGjeOedj+jUsSP33P9XPvhwFp/NXcDFl/7G2n28evgeJa1qgM0mp8sa9O0/kklXnM+br7/Lrh3ZXD7pem64aTJjxw7HZrfx/HP/Znv2dkpKy/hkzgf8/YmnWb9uI3M//4q3/vMMjz0ylaVff8btf/6L0mSHDhvIDz/+xMUXD+CbpYu54YZb8cS6OOP0idw05UYuvvAyQiYUFRRxyqnH8cDDj2OzO3A6HWqX9osvup5b/3wjDpuDW265g/FHjyZr/Sa6duvEm2+9Rk7ODi6fNBmXw0Ze/m7OOHMi9973ILNmvsPf7nlEkcVddz7EqwIKPokAAAy1SURBVK8/j7eqgjNPv5Sx40ayedMWPB4P48YfxYIvl7AzZxcffvQ2JcVFnH/OFXy1aBZbv13DtdfcQP8BfSgrqSTWE09CQgKLvvqU2267g/btOnLf357gXy/+g8xevWrMiUVJu2oxNAIagVoINIGZzs1HM+ficLkoL/eTnpGqCKawYCffr1jB8q9X8M+nH+Oz+TOZdMWVzP74Q1auXE/7DumkJqfx6stvccGFZzBu/BEMGjSEyddP4dLLzsFmc7Lgy6/45JN5nHHG6XTt3hOv16tG21YNxIwkd7LtuXWujRUg2o2LefPns2jxcp7711P866VXMAwbr732lpprmv3RHHp070n2tgI6dmjPB+/L6VmSX8SOVAujw/tgGpjCCEprCxCfkEDAH1QaR0VFFV6fODDYqCgv59rJl/PuB6+zcePPLPt6GVdddRk//rCGndlr+GjmHCZMmMDWLdt47tmXeP6Facz417O4YzwEAkFFZlu2bOWGm37LLX/+fzz59yfZsiWbuZ99zNRpD/LU1OmsXbOcuLh4MC0zXFlFBT5/CDG9lpSWcN+DdzLz4zf5bO5XzJ0zixeff5m83Dw+nTeHBx+5l8efeJrVq5cxYNAQLrnsYgYO7K/kWbTwK5wuJ4UFJdz0h2sVOX311VJ69OjGp599QHFhOYsXLMTutFPhraC8opK/3fsQRxw5gnfen8XRx4yivKIcny/A448+RZwnnquvuZIfflzJ9Ode3GPWPbwtqUvXCGgEGkDg0DQj1XnLRPrnBAMhfvOb3yKnk4YCXj6b+wUdO2ZgGiaGzSA2Lp64uATKSqtw2FzYnYYioOHD+uLzBakqK8cWpsaM9j04+dTjeeKJ59iVk8Ojj4qPhYEM0w3lLSU1Em0hkYED+7BgwZKwV1kaf77lD1RUVHLMCWOVyc6tTv6044pxY7PZ2LZlJZs2bqGsopJLLplEVZWX7B3Z5ORspl27juF8GkCshV+FCOKMkfkuMU/6WbLwG9p3aEdKWqoiAamT8KjL5aJd+wzaJHpITkpV2tHpZ5xLj55dmfrkM2St28Ddd93G9uwduJxOevbojMedSreuXfD5/ARDQZKTkjh94inExSWycdPPdOrcEcOWQI/MrthsdnbuyMGhvjFCQAZ2uwObgUqblp5Oj+5iBg2SlNSGrVt2kL19O927dlKebr16dVOn5BYWFPLN19/xwYcfcsG5ZxPricWQeSIzhCc+hox2acS4Y0hMakO37l0VSbVtK84tTvUdcDjFpFjBjpw8xh8zXrXGoKGDhI8pLy+nqLCMQMDL3E/ncPHF59OvnxyqU9nCraaL0whoBA4UgUPUjGJZtvRr5n7yBS+8+CTzP/+UufPmcuJJx/L3x59h4KAB9M7syb13P8bJJ5zJY48+wPEnHkNcrAu7abB25Wq2b8vGE9uO2Nh4Fi5YykcfvqHmFK66+hIWfLEIl8PF0ceMI+Avobi4mMpK6VjEFVmqGuTGm66jrKSUC8+9kj/e9DueenI6PXp05uSTJ9Kteydu/dMd3Hf3n8nPzeOySRfy1NTnSM9I5rN5M5n3+ce8+97L7MrZzdtvfRju8A8UwuaILxqaoYjcH4BFS5bx1FNPcMkF5zFvzufcetsfiIvzUFxYit/rJxj0U1BYRFWVT2kHRUX5VFXKqbtuLrz4HP7x1AtqzmbAoKH06Z2J0+Xg+Rmv8cmst1i4aKGqgN9vUlxcRFmZeFGaTJhwAit/WM3cT95jxnOvkpTclqHDhrM7v5jyigq13Ehw93m9xLg87NyZx0svvcKrL/2Hgt27GX/0KI47frzSkud/9iH/mv4yGelp9O8/iLfeeIe4uDYMHT6I/Pw8/H6pg0lxUQlerw+/L0BRQYkaKIjbenFxKT5/lZqTknmltm3bcPS4Ubz/7gcsXDCfl196g/LSCmTeqGv3jrg9Hq645iqVPrOXEKTg2QgPu+ZoSp2nRkAj0CgEDs2127Art9oBg/pw4cVn4fG4cbtj6dOnq5onGjduJKdOPIkfvv+R4cOHcOddt9Gpc0+OGj2YhQsWk5ySyu9vvJY2SQn06d2ViqoqYmNj1OR1WmpbXn7xP5x1zkROPPlMQqFy2iQmMnrMkXTu0kE5KIg7drv2XTnttOPZumUrfn+AO+7+I5dfcSkxMR7OOO0kNm7YSFFhIQ89chdDho5gZ3Y2F11yDv0GDMHjtpOWlkbnzu1p1y6dPn3Cx6c3CrrmjBQ2QZomubtyw44BWaQkp/DQo/dw6sTT8XpL+fnn7WqOpVOn9uTszGXiaSeqDlmwOOaY0XTrnklaegLTp7/CVddcwthxx9M2KZHefbrz5hvvE/D7GHnUcPr370Wf3j0pLS1mwsQTiIuPYfDggSTEu3npxVcoKi7liakP0LvPEH7eupEuXTswZuyRbNm8laOPHkd+Xi6rV/5Ex47pzJw5mz/96SZOmXgqAwaKM4qLf7/4shpEPPHkA2T2GkTnTmksWLCIgvx8jj52NEOHDaJjx3bk5uYyYeJJuN0x7MjO5uRTjiMjI51NmzYzbuwopRHKoOK000/mhBOP4/tvV7Jk4SLGjjuCjh3S1bzW+GPG8f133/Huf9+jc5fOnH/+OcTGilZVZw2ZeOnpSyOgEYgaBBo4QmJXI4SUTlMWG8pCRFloKj94cd2WZw+YhWGX6ogHnCxW9FluxEgHIaPVCmvRpFp8KR2EjOhNPp83l3POuIT5Cz5i+BGjABmxy6LXKnXkuTXaFRFFBilPTFkyApbjz8vDC0Ol3EjZcjR6meXqLXHkPuJhJW7nsk5GhUXTvFGkbhEFVmxkETmluhG8pM5yLxhJG0h9xGvNzcz/vcuFF13Fd98tpG+/AeE44jYvc2sy9yN/kYWzgpW0kbShhIv7t2ii0lZiDiy13LxFazMrLJduYnn8kbt48onp/LxjJXaHtIWY3YpruJBLHrL+R5qrPCy3LE6Wekne8l7qIHJJu8j3QsoOL+IVN20lo6SR/GXBrWAhf1IP+Q6GLK85Zc5zWg4LCh/JQ+LUaVd9hITVHvq/RiBKEFAzAPXLUufHW28kwyIX1VFEIkiYdC7yJ/2KdIqR1f2Sp3RqkQ5HnmX2QdLUiGe46NAhjTfffkGNmq0dF6SDKowUEu6wJH2d8qpjRPIUOSJ1kbCScAzpCMOmG+k4q69wWPXz4boJ1y2Co6pnXdmEdMPyGUIici9rc2QnAvkMqDmdBx+4k76RuRMJF9JSkNRw/JC0Ko9whmZ4Jwu1JkkIMKJZWG1pISrkF2DsuNEYNpsyF9od3rArtWAteQmBSWzZOUIVEiYNCRNza/h7okSP7KBQRxZFkJF6Sp1FliAYMnCRbPx7mlh205BwkVvIU4FiSbsHrHBe+kMjoBGIGgQa1oxkYlmNtEXeyOg8Irt0LBLmDy+QjPzgI7//cMej4si9XNJBSUciI/4ID4afq6OEOyk1khZtp+bWL5F34ez0Rx0EIm1ggSmLTmW3BktzKAz3xZE4NZNGwK8ZVvO+Idwj2pu0VUQ7rpn2AO8je98p0jzAtLWiR+q5j7oZ7WrF1g8aAY3A4UWgATIqo7S0BKfLhc/nI+APKG80caOWn7d4cXmrqtSiS8tcEvnRC0EJwUAw6FXpHA5HOK2JzS7mJC+lJZY2EhcXh80uJhyL7GShpcPuwLBJWGREbuUdKSHSNUY+paz93dftmuo+R5qhZnh995F48inyROLUfa75rqH7SH5185HwSFgkvXxGwuu/N8TRvRYW8mD17/JOLnmv9kZQJUgZkfyttypSddk1w+S+rkwqRAoICxTJK/xYK37N9FYp1clUvJppIveReJG0NcPryhJ5F6lT3TS14qsdPmrmru81AhqBw4nAPskoEAjw6KOPMmTIEDp16sTixYvVRHr79u3VItL09HQWLVqE7J+WmNiGiopy1R/ZDAOHw6ncqnv27MHyFcuJccWoNUKhUIhgMET//v0UwRUWFlJaWkpKSoqy4JSVlZKdnY3kbXc46NmjB6NHjz6c+OiyNQIaAY2ARqAFENgnGQlx/PDDj6SmpigCKS+X9RsBRJPp2LGTWoUvZLJrVy6VlRVq9bu46Aq5yJqXxMREkpOTFQlt3LiRrVu3MnLkSPLy8sjMzFRVy8/fTSDgV8Qk2lNVVRXyKbsNyGd6egYdO4rnnL40AhoBjYBGoDUjsE8yas2V1nXTCGgENAIagehCoK5XQnRJp6XRCGgENAIagV8FApqMfhXNrCupEdAIaASiGwFNRtHdPlo6jYBGQCPwq0BAk9Gvopl1JTUCGgGNQHQjoMkouttHS6cR0AhoBH4VCGgy+lU0s66kRkAjoBGIbgT+P7ti6HFJTpvtAAAAAElFTkSuQmCC />"
Question 3Which of the following best describes the role of NAD+?
1.It is used as an electrophile in metabolic processes.
2.It is used as a Brnsted Lowry acid in metabolic processes.
3.It is used as a reducing reagent in metabolic processes.
4.It is used as an oxidizing agent in metabolic processes.
5.It is used as a nucleophile in metabolic processes.
Question 4Under aerobic conditions, what happens to pyruvate after it is formed in glycolysis?
1.It is excreted from the body.
2.It is converted to ethanol.
3.It is converted to lactic acid.
4.It is converted to acetyl-CoA.
5.It is converted to NAD+.
Question 5The product of the following reaction is:
![]()